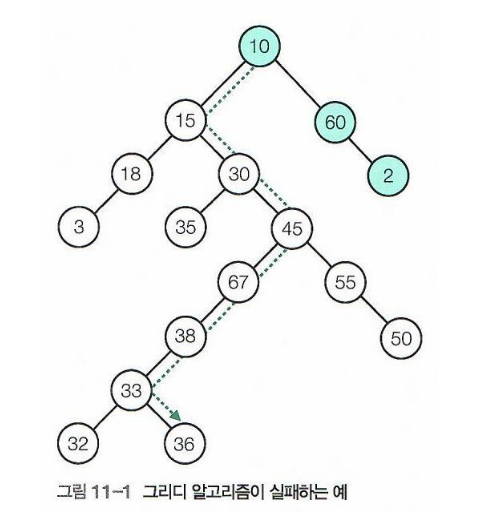
1. 그리디 알고리즘

그리디 알고리즘은 Greedy(탐욕, 욕심쟁이)라는 이름처럼 지금 당장 최적인 답을 선택하는 과정을 반복하여 결과를 도출하는 알고리즘이다.

그리디 알고리즘은 말 그대로 각 단계에서 미래를 생각하지 않고, 그 순간 가장 최선의 선택을 하는 기법이기 때문에 종합적인 결과에 대해서는 최적의 해를 보장할 수 없다. (지역적(local)으로는 최적의 선택이지만 이를 반복하더라도 전체적(global)으로는 최적의 해가 아닐 수 있음)

순간 순간 최적이라고 생각되는 것을 선택해 나가는 방식으로 최종적인 해답을 찾지만 그것이 최적이라는 보장은 없다.

2. 그리디 알고리즘의 장점

1.최적의 해를 보장할 수 없음에도 Greedy 알고리즘을 사용하는 이유는 해당 알고리즘의 계산 속도가 매우 빠르기 때문이다.

2.탐욕 알고리즘은 근사 알고리즘으로 사용이 가능할 수 있으며, 대부분의 경우 계산 속도가 빠르기 때문에 실용적으로 사용할 수 있다.

하지만 어느 정도까지 최적해에 가까운 해를 구할 수 있는지를 보장하려면 엄밀한 증명이 필요하다.

3. 그리디 알고리즘 적용을 위한 2가지 조건

1. 탐욕적 선택 속성(Greedy Choice Property)

앞의 선택이 이후의 선택에 영향을 주지 않는다.

2. 최적 부분 구조(Optimal Substructure)

문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성

위 조건이 성립하지 않는 경우에는 그리디 알고리즘은 최적해를 구하지 못한다.

그리디 알고리즘을 적용하여 최적해를 구할 수 있는 간단한 문제인 동전 문제를 예시로 해당 두 조건을 설명하겠다.

지불해야 하는 값이 x 원 일 때 1원, 50원, 100원, 500원 동전을 이용해 값을 지불하시오.(사용되는 동전의 수가 최소가 되어야 함)

해당 문제는 가장 큰 동전부터 최대한 지불해야 하는 값을 채우는 방식으로 구현이 가능하다.

탐욕적 선택 속성(Greedy Choice Property)의 만족

각 선택이 이전 선택에 관계없이 나머지 금액을 최대로 채울 수 있는 동전의 갯수를 선택하기 때문에 현재 선택이 이후의 선택에 영향을 주지 않는다는 탐욕적 선택 속성조건을 만족한다.

최적 부분 구조(Optimal Substructure)의 만족

500원 ->100원->50원->10원, 큰 동전에 먼저 선택권을 부여하기 때문에 매 순간 나머지 금액을 최대로 채우는 선택이 결국 가장 최소의 동전 개수를 도출한다는 점에서 최적 부분 구조 조건을 만족한다.

매트로이드 구조의 문제에 대해서는 그리디 알고리즘이 언제나 최적해를 찾아낼 수 있다.

매트로이드 이론

• Greedy Algorithm(그리디 알고리즘)이 Optimal Solution(최적해)을 가려낼 수 있는 경우인지를 판별할 수 있게 하는 수학적 공간이다.
  매트로이드설명

4. 참고문헌

https://dad-rock.tistory.com/663
https://it-college-diary.tistory.com/entry/21-Greedy-Algorithm%ED%83%90%EC%9A%95%EB%B2%95-%EC%9A%95%EC%8B%AC%EC%9F%81%EC%9D%B4-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EA%B0%9C%EB%85%90
https://kahee.github.io/algorithm_datastructure/2018/03/14/Algorithm_greedy_alogrithm
https://geunuk.tistory.com/74
https://kahee.github.io/algorithm_datastructure/2018/03/14/Algorithm_greedy_alogrithm/
https://rlakuku-program.tistory.com/39