[DIP] 직선을 원으로 변환하기 1

코드짜는침팬지·2023년 7월 26일

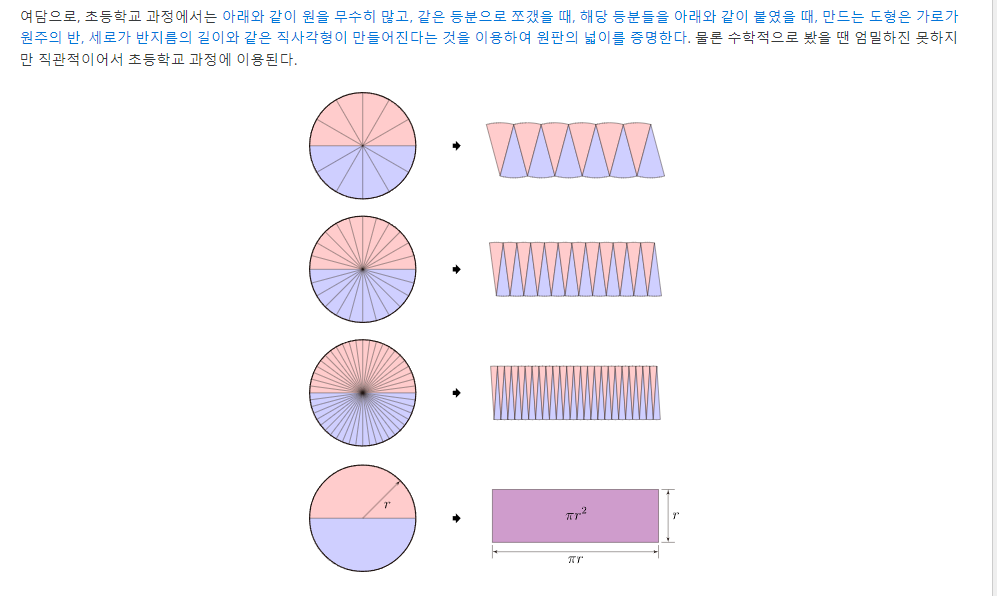
원을 직선으로 만들려면, 직선을 원으로 만들려면 어떻게 해야할까?

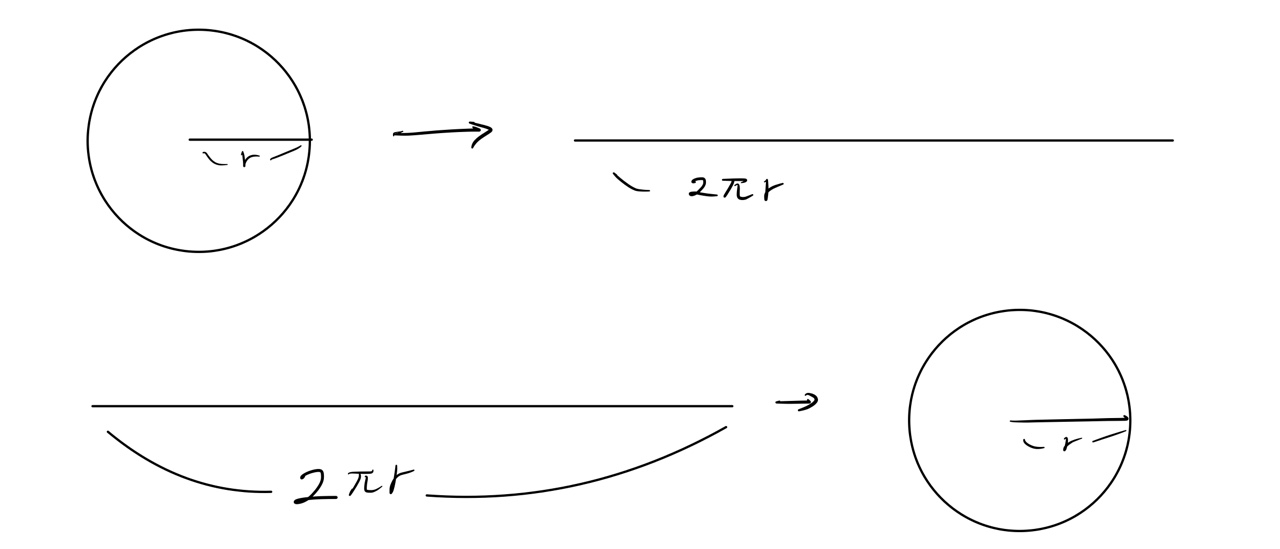
나무위키 원
나무위키 좌표계
다음 두가지에 있는 지식들만 알면 정말 간단하게 할 수 있다.

위에 나온건 사실상 적분이다. 컴퓨터로 적분계산은 크게 어려운게 아니다.
우리가 쓰는 for문이 적분과 비슷한 역할을 해주기 때문이다.

\displaystyle\sum_{i=1}^{k+1}i \displaystyle \displaystyle= \left(\sum_{i=1}^{k}i\right) +(k+1)

핵심은 극좌표계와 직교좌표계의 변환이다.
아무튼 직관적으로 생각했을 때 우리가 해야하는건 중심점을 기준으로 직선을 말아줘서 동그라미를
만드는 것이다.
모든 픽셀에 대해서 직교 좌표계에서 극좌표계로 변환을 해주는데
이걸 모든 픽셀에다가 적용 한다는 개념이다(적분)

문제는 어떻게 이걸 말아 줄 것이냐 인데 for문을 쓰는 방법과 파이썬 내부의 이미지 배열 전체를 한 번에 처리하는 방법이 있다. 연산속도는 당연히 배열 내부에서 처리하는게 훨씬 빠르다.

일단 직관적인 이해를 위해 for문을 써서 해보자
이 코드는 for문을 이용해 직교좌표계를 극좌표계로 변환하며 변환 방법은 다음과 같다:

새 이미지 (polar_image)의 모든 픽셀에 대해 반복문을 실행한다. 이때 새 이미지는 원본 이미지의 두 배 크기이다.
각 픽셀의 위치 (x, y)에 대해, 그 위치의 극 좌표 (radius, theta)를 계산한다. 여기서 radius는 원점 (center)에서 해당 픽셀까지의 유클리드 거리이며, theta는 원점에서 해당 픽셀까지의 각도이다.

$\text{{radius}} = \sqrt{(x - \text{{center}}[0])^2 + (y - \text{{center}}[1])^2}$

$\text{{theta}} = \arctan2(y - \text{{center}}[1], x - \text{{center}}[0])$

계산된 극 좌표 (radius, theta)를 다시 원본 이미지의 직교 좌표 (x1, y1)로 변환한다. 이 변환은 아래 수식을 사용하여 수행한다.

$x1 = \left\lfloor \frac{{(\text{{theta}} + \pi) / \pi \times ((int(height)/4)}}{2} \right\rfloor$

$y1 = \left\lfloor \text{{radius}} \right\rfloor$

계산된 (x1, y1)가 원본 이미지의 크기 내에 있다면, 원본 이미지의 (y1, x1) 픽셀 값을 새 이미지의 (y, x) 위치에 복사한다. 그렇지 않다면 해당 픽셀은 0 (검은색)으로 남게 된다.

위 수식에서, x1의 계산은 theta ([-pi, pi] 범위)를 [0, 1] 범위로 정규화한 후, 원본 이미지의 폭을 기준으로 스케일링한다.

import numpy as np
import cv2
from scipy.ndimage import map_coordinates
import matplotlib.pyplot as plt
from skimage.transform import AffineTransform


def linear_polar(image):
    # Get the dimensions of the image
    height, width = image.shape[:2]

    # Create an empty output image
    polar_image = np.zeros((height*2, height*2), dtype=image.dtype)
    center=[height, height]

    # Calculate the maximum radius
    max_radius = 100

    # Create arrays to hold the Cartesian coordinates
    
    polar_image[0, 0] = image[0,0]
    # Convert the Cartesian coordinates to polar coordinates
    for y in range(height * 2):
        for x in range(height * 2):
            radius = np.sqrt((x - center[0])**2 + (y - center[1])**2)
 #이 식에서, (x, y)는 극 좌표계에서의 픽셀 위치이고, center는 극 좌표계에서의 중심 위치이다. 
 #즉 radius는 (x, y) 픽셀이 중심으로부터 얼마나 떨어져 있는지를 나타낸다.
            theta = np.arctan2(y - center[1], x - center[0])
#이 식에서도 마찬가지로, (x, y)는 극 좌표계에서의 픽셀 위치이고, center는 극 좌표계에서의 중심 위치이다. 
#np.arctan2는 두 인자의 비율에 대한 아크탄젠트 값을 반환하므로, 
#이 식은 (x, y) 픽셀이 중심에 대해 어느 각도에 위치하는지를 계산한다.    
#함수는 [-pi, pi] 범위의 값을 반환하므로, theta + np.pi를 해주는 이유는 theta의 범위를 [0, 2pi]로 바꾸기 위함이다. 
#이렇게 하면 각도 값이 항상 양수가 되어 처리하기 더 편리하다.        
            x1 = int(((theta + np.pi) / np.pi) * (height / 2 ) #+ 533/4
            y1 = int(radius)
            if x1 >= 0 and x1 < width and y1 >= 0 and y1 < height:
                polar_image[y, x] = image[y1, x1]
#이 두 식은 극 좌표계에서의 좌표 (radius, theta)를 원본 이미지의 직교 좌표계로 변환한다.

#x1은 theta 값을 원본 이미지의 너비 범위로 스케일링한다. (theta + np.pi) / np.pi는 theta의 값을 [0, 2] 범위로 정규화하고, 
#그 후에 원본 이미지의 너비 (height / 2)를 곱하여 스케일링한다.

#y1은 radius 값을 사용하고 있다. 즉, 원본 이미지에서의 y 좌표는 극 좌표계에서의 radius와 동일하다 가정한다. 
#이 가정은 이미지의 중심이 극 좌표계의 원점과 일치하고, 
#이미지가 원형 영역에 근사하게 분포되어 있는 경우에 유효하다 상황에 따라 코드를 수정해야할 수 있다.

#마지막으로, 계산된 (x1, y1) 값이 원본 이미지의 범위 내에 있는 경우에만 해당 픽셀 값을 polar_image에 복사한다. 
#이는 변환된 좌표가 원본 이미지의 범위를 벗어나는 경우를 방지하기 위한 것.
                
               

    return polar_image



src = cv2.imread("C:/Users/joong/OneDrive/Documents/code_projects/RatelSoft/data2/Test_img/rotate2-3mm.BMP", cv2.IMREAD_GRAYSCALE)



lp = linear_polar(src)
cv2.imshow("lp", lp)
cv2.waitKey(0)
cv2.destroyAllWindows()