Titans: Learning to Memorize at Test Time 번역

대학원

목록 보기

3/3

Abstract (초록)

오랜 기간 동안, 재귀(Recurrent) 모델과 어텐션(Attention)을 어떻게 효과적으로 활용할지에 대한 광범위한 연구가 이루어져 왔습니다. 재귀 모델은 데이터를 고정 크기의 메모리(‘은닉 상태’라고도 함)에 압축하고, 어텐션은 전체 컨텍스트 윈도우를 참조해 모든 토큰 간의 직접적 의존성을 포착합니다. 이렇게 더 정확한 의존성 모델링을 제공하는 어텐션은 쿼드러틱( $O(N^2)$ ) 비용을 요구하므로, 컨텍스트 길이에 제약이 생기게 됩니다.

본 논문에서는 과거(역사적) 컨텍스트를 학습해 기억하는 새로운 뉴럴 장기 메모리 모듈을 제안합니다. 이 모듈은 어텐션이 현재 컨텍스트에 집중하는 과정에서 오래된 과거 정보도 함께 활용할 수 있도록 돕습니다. 또한 병렬화가 가능한 빠른 학습과 빠른 추론을 동시에 달성할 수 있음을 보입니다.

메모리 관점에서, 어텐션은 컨텍스트 윈도우는 제한되지만 의존성을 매우 정확하게 모델링하므로 ‘단기(short-term) 메모리’, 반면 우리의 뉴럴 메모리는 데이터를 장기간 저장할 수 있으므로 ‘장기(long-term)·영속(persistent) 메모리’ 역할을 한다고 주장합니다. 이 두 모듈에 기반하여, “Titans”라는 새로운 계열의 아키텍처를 제안하고, 세 가지 변형(variant)을 통해 장기 메모리를 효과적으로 통합하는 방법을 논의합니다.

언어 모델링, 상식 추론, 게놈(유전체) 데이터, 시계열 예측 등 다양한 실험 결과, Titans가 트랜스포머(Transformers)와 최신 선형 재귀 모델들을 능가함을 확인하였습니다. 또한 2백만(2M) 이상의 컨텍스트 길이로도 확장 가능하여, “건초더미 속 바늘 찾기(needle-in-haystack)” 유형 과제에서 기존 대비 더 높은 정확도를 달성했습니다.

Introduction
Preliminaries
- 2.1 Backgrounds
Learning to Memorize at Test Time
How to Incorporate Memory?
Experiments
Conclusion
References
Appendix

1 Introduction

“진정한 기억 기술의 핵심은 주의(attention)의 기술이다!”
— Samuel Johnson, 1787

배경

트랜스포머(Transformers) [Vaswani et al.]는 대규모 학습에서의 인-컨텍스트 러닝(in-context learning) 능력 및 강력한 표현력 덕분에 순차 모델링의 사실상 표준이 되었습니다 [Kaplan et al. 2020].
트랜스포머의 핵심인 어텐션(attention) 모듈은 연상(associative) 메모리로 볼 수 있습니다 [Bietti et al. 2024]. 즉, 키-값(key-value)을 저장하고, 쿼리(query)-키 유사도를 통해 필요한 정보를 가져옵니다.
다만, 이 정확한 의존성 모델링은 컨텍스트 길이가 $N$ 일 때 $O(N^2)$ 의 시간 및 메모리 비용을 요구하므로, 긴 시퀀스가 필요한 작업(예: 대규모 언어 모델링 [Liu et al. 2024], 비디오 이해 [Wu et al. 2019], 장기간 시계열 예측 [Zhou et al. 2021])에서 트랜스포머 사용이 어려울 수 있습니다.

한계점과 최근 연구 동향

트랜스포머의 확장성 문제를 해결하기 위해, 선형 트랜스포머(linear Transformers) [Katharopoulos et al. 2020, Kacham et al. 2024, Yang et al. 2024] 등이 제안되었습니다.
- 소프트맥스를 커널 함수를 이용해 대체하여 메모리 사용량을 크게 낮추고 긴 컨텍스트로 확장 가능하다는 장점이 있지만, 실제 성능은 여전히 일반 트랜스포머와 격차가 있습니다.
- 선형 트랜스포머는 결국 재귀 신경망(RNN)과 유사한 구조를 가지며, 과거 정보를 작은 상태(state)에 압축하기 때문에 긴 문맥 정보를 충분히 담기 어렵다는 지적이 있습니다 [Wang et al. 2024].
뿐만 아니라, Hopfield Network [Hopfield 1982], LSTM [Hochreiter & Schmidhuber 1997], 트랜스포머 [Vaswani et al. 2017]를 비롯한 다양한 모델들이 실제 문제에서 필수적인 일반화·추론·길이 추론 등에서 한계가 제기되고 있습니다 [Anil et al. 2022, Qin et al. 2024].
- 인간 두뇌처럼 “단기·작업·장기 메모리, 메타 메모리” 등 여러 모듈이 서로 협력하고 독립적으로 작동하는 구조가 필요하다는 통찰이 제기됩니다 [Cowan 2008].

메모리 관점

메모리는 학습의 필수 요소입니다 [Terry 2017].
RNN은 은닉 상태를 “메모리”로 간주할 수 있습니다. 각 입력이 들어올 때마다 메모리를 갱신하고 필요한 정보를 조회한다는 점에서, 트랜스포머의 키-값도 마찬가지로 “(압축 없이) 확장되는 메모리”로 볼 수 있습니다.
이 관점에서 선형 트랜스포머와 일반 트랜스포머를 비교하면, 전자는 과거 데이터를 고정 크기 행렬에 압축해 저장하고, 후자는 (설정된 창 범위 내에서) 모든 데이터를 저장합니다.

이러한 비교에서 떠오르는 질문:

(Q1) 좋은 메모리 구조란 무엇인가?
(Q2) 올바른 메모리 갱신 방식은?
(Q3) 적절한 메모리 검색 과정은?
(Q4) 서로 다른 유형의 기억 모듈을 어떻게 결합할 것인가?
(Q5) 긴 과거를 저장하기 위한 깊은(Deep) 메모리가 필요한 것은 아닐까?

기여 및 구성(Contributions and Roadmap)

이 논문에서는 위 다섯 가지 질문에 답하기 위한 연구를 전개합니다.

뉴럴 메모리 (§3)
- 딥(Deep) 뉴럴 장기 메모리 모듈을 소개합니다. 이는 테스트 시점에서 데이터를 암기할 수 있는 “메타 in-context” 모델입니다.
- 인간 장기 기억 체계에서 착안해, “놀람(surprise)이 큰 이벤트가 더 잘 기억된다”는 점을 이용합니다. (3.1절)
- 한편, 메모리 용량을 고려한 망각 기제(forgot)를 설계해 필요 없는 정보를 지울 수 있게 했습니다.
- 이 메커니즘을 미니배치 경사하강 + 모멘텀 + 가중감쇠(weight decay)로 구현할 수 있음을 보이며, 병렬 연산(matmul)을 이용해 빠른 학습이 가능함을 제시합니다.
Titans 아키텍처 (§4)
- 제안된 장기 메모리 모듈을 전체 모델에 통합하는 방식으로 Titans 계열을 제안합니다.
- (1) 코어(Core): 단기 메모리(어텐션)로 구성된 주 처리부, (2) 장기 메모리: 우리가 설계한 뉴럴 메모리, (3) 영속적(persistent) 메모리: 태스크에 대한 지식을 입력과 무관하게 저장하는 파라미터.
- 이 구조를 활용해 (i) 컨텍스트로서 메모리를 사용, (ii) 게이트로 결합, (iii) 레이어로서 메모리를 쌓는 등 세 가지 변형을 제안합니다.
실험 결과 (§5)
- 언어 모델링, 상식추론, “건초더미 속 바늘(needle-in-haystack)”, 시계열 예측, DNA 모델링 등에서 Titans를 평가했습니다.
- Titans는 트랜스포머 및 현대 선형 재귀 모델들보다 전반적으로 우수하며, 특히 매우 긴 컨텍스트(2M 이상)에서도 높은 정확도를 보였습니다.

2 Preliminaries

이 절에서는 본문 전체에서 사용하는 기호와 주요 배경을 정리합니다.

$x \in \mathbb{R}^{N \times d_{\text{in}}}$ : 입력 데이터
$\mathcal{M}$ : 뉴럴 메모리 모듈
$\mathbf{Q}, \mathbf{K}, \mathbf{V}$ : 어텐션의 쿼리·키·값 행렬
$\mathbf{M}$ : 어텐션 마스크
시퀀스 분할 시, $S(i)$ 는 $i$ 번 세그먼트, $S_j(i)$ 는 그 세그먼트의 $j$ 번째 토큰
$\mathcal{N}(x)$ : 뉴럴 네트워크 $\mathcal{N}$ 의 정방향 계산(가중 업데이트 포함)
$\mathcal{N}^*(x)$ : 뉴럴 네트워크 $\mathcal{N}$ 의 순전파(가중 업데이트 없음)
$\mathcal{N}(k)$ : 뉴럴 네트워크의 $k$ 번째 레이어

2.1 Backgrounds

어텐션(Attention)

트랜스포머 [Vaswani et al. 2017]는 입력 $x \in \mathbb{R}^{N \times d_{\text{in}}}$ 에 대해,

\mathbf{Q} = x \mathbf{W}^Q, \quad \mathbf{K} = x \mathbf{W}^K, \quad \mathbf{V} = x \mathbf{W}^V

y_i = \frac{ \sum_{j=1}^{i} \exp\Bigl(\frac{\mathbf{Q}_i^\top \mathbf{K}_j}{d_{\text{in}}}\Bigr)\,\mathbf{V}_j }{ \sum_{\ell=1}^{i}\exp\Bigl(\frac{\mathbf{Q}_i^\top \mathbf{K}_\ell}{d_{\text{in}}}\Bigr) }

로 계산됩니다. 이는 컨텍스트 길이 $N$ 에 대해 $O(N^2)$ 연산과 메모리를 사용합니다.

효율적 어텐션(Efficient Attentions)

소프트맥스 대신 특정 커널 함수를 사용해 계산량을 줄이는 선형 어텐션 [Katharopoulos et al. 2020, Kacham et al. 2024, Yang et al. 2024]이 존재합니다.
$y_i = \frac{ \phi(\mathbf{Q}_i)^\top \sum_{j=1}^i \phi(\mathbf{K}_j)\mathbf{V}_j }{ \phi(\mathbf{Q}_i)^\top \sum_{\ell=1}^i \phi(\mathbf{K}_\ell) }$
여기서 $\phi$ 가 특정 조건( $\phi(\mathbf{x}, \mathbf{y}) = \phi(\mathbf{x})\phi(\mathbf{y})$ )을 만족하면, 재사용(누적) 계산이 가능해집니다.
$\phi$ 를 항등함수(Identity)로 두면,
$\mathcal{M}_t = \mathcal{M}_{t-1} + K_t^\top V_t, \quad y_t = Q_t \mathcal{M}_t$
형태의 재귀적 표현이 가능해집니다.

메모리 모듈(Memory Modules)

메모리는 초창기부터 신경망 설계의 핵심이었습니다 [Hopfield 1982, Hochreiter & Schmidhuber 1997, Graves 2014 등].
Fast Weight Programs [Schmidhuber 1992, Munkhdalai 2019] 등은 키-값(연상) 메모리를 재귀적으로 학습하는 전통이 있으며, Hebbian [Hebb 2005] 또는 Delta [Prados 1989] 규칙을 많이 활용합니다.
다만 대다수는 “단일 시점 놀람(momentary surprise)”에만 의존하거나, 망각 게이트가 없어 장기 메모리 관리에 한계가 있습니다.

3 Learning to Memorize at Test Time

이 장에서는 테스트 단계에서 데이터를 학습(암기)하기 위한 뉴럴 장기 메모리 모듈을 제안합니다.

3.1 Long-term Memory

학습 과정 및 놀람 지표(Surprise Metric)

장기 메모리를 온라인 학습 문제로 바라보고, 과거 $\{x_1,\ldots,x_{t-1}\}$ 를 메모리에 저장한다고 합시다.
인간이 “예상치 못한(놀람) 이벤트”를 더 잘 기억한다는 점 [Mandler 2014]에서 착안해, 입력 $x_t$ 에 대한 모델(메모리) 손실 $\ell(\cdot;x_t)$ 의 기울기 $\nabla \ell$ 이 큰 경우 더 놀랍다고 정의할 수 있습니다.
이를 단순히 $\mathcal{M}_t = \mathcal{M}_{t-1} - \theta_t\,\nabla \ell(\mathcal{M}_{t-1};x_t)$ 로 업데이트할 수도 있으나, 순간 놀람이 커지면 그 뒤 시점에서는 기울기가 사소해져서 중요한 정보를 놓칠 수 있습니다.

모멘텀 기반 놀람

위 문제를 해결하기 위해, “과거 놀람 + 현재 놀람”을 함께 고려하는 모멘텀(momentum) 용어를 도입합니다: $\mathcal{M}_t = \mathcal{M}_{t-1} + S_t, \quad S_t = \eta_t\,S_{t-1} - \theta_t\,\nabla \ell(\mathcal{M}_{t-1};x_t).$
$\eta_t$ 가 과거 놀람의 영향을 얼마나 남길지(0에 가까우면 완전 무시) 결정합니다.

손실(Associative Memory Loss)

우리는 메모리를 “키-값 연결(associative) 메모리”로 설계합니다: $\mathbf{k}_t = x_t\,W^K,\quad \mathbf{v}_t = x_t\,W^V,$ $\ell(\mathcal{M}_{t-1};x_t) = \|\mathcal{M}_{t-1}(\mathbf{k}_t) - \mathbf{v}_t\|_2^2.$
이는 $\mathbf{k}_t \mapsto \mathbf{v}_t$ 를 정확히 학습하도록 하는 목표입니다.

망각(Forgetting) 메커니즘

긴 시퀀스에서 모두 저장하기 어렵기에, 다음과 같은 게이트를 추가해 메모리 용량을 관리합니다: $\mathcal{M}_t = (1-\alpha_t)\,\mathcal{M}_{t-1} + S_t,\quad S_t = \eta_t\,S_{t-1} - \theta_t\,\nabla \ell(\mathcal{M}_{t-1};x_t).$
$\alpha_t$ 는 망각 정도를 결정하며, 1에 가까울수록 과거 정보를 제거하는 효과가 커집니다.

메모리 구조

본 논문에서는 단순 MLP( $L_\mathcal{M}\ge1$ )로 구성했습니다.
선형 메모리(행렬 형태)보다 딥(Deep) 구조가 더 표현력이 높을 수 있으며(§5.5), 향후 더 정교한 구조로 확장 가능하다는 여지를 둡니다.

메모리 조회(Retrieving)

입력 $x_t$ 를 쿼리 $\mathbf{q}_t = x_t\,W^Q$ 로 투영한 뒤, 메모리에 정방향 계산(가중 업데이트 없이)을 수행해 $y_t = \mathcal{M}^*(\mathbf{q}_t)$ 로 필요한 정보를 얻습니다.

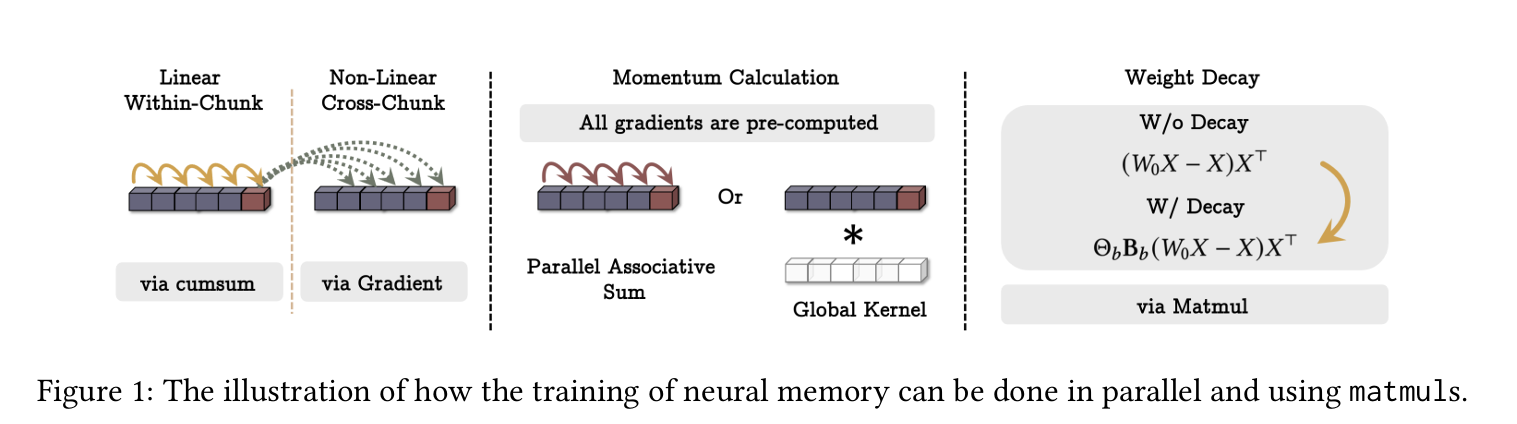
3.2 How to Parallelize the Long-term Memory Training

위 장기 메모리 갱신은 이론적으로 $O(N)$ 이나, 실제로는 하드웨어 가속의 이점을 살리기 위해 텐서(matmul) 연산으로 병렬화가 필요합니다.
$\mathcal{M}_t = (1-\alpha_t)\,\mathcal{M}_{t-1} - \theta_t\nabla\ell(\mathcal{M}_{t-1};x_t)$ 와 같은 형태를 미니배치 경사하강으로 묶어 계산하면, [Sun et al. 2024]에서 논의된 것처럼 큰 행렬 곱으로 처리할 수 있습니다.
$\eta_t,\theta_t,\alpha_t$ 를 토큰별로 다르게 두는 대신, 청크 단위로 고정해도 추가 효율을 얻을 수 있습니다(파라미터가 청크별 스칼라).

3.3 Persistent Memory

제안한 장기 메모리는 입력 의존적(Contextual)입니다. 그러나 태스크 관련 지식 등은 입력과 무관하게 저장해야 할 수도 있습니다.
이를 위해 영속적 메모리(persistent memory) [Sukhbaatar 2019] 파라미터 $P = [p_1,\dots,p_{N_p}]$ 를 두고, 실제 입력 앞에 붙이는 방식을 사용합니다: $x_\text{new} = [p_1,\ldots,p_{N_p}] \,\|\, x.$
이는 (1) 장기 메모리와 달리 “항상 유지되는” 태스크 지식 저장, (2) 트랜스포머의 FFN과 유사하게 동작, (3) 초반 토큰에 과도하게 집중되는 현상을 완화하는 장점이 있습니다.

4 How to Incorporate Memory?

장기 메모리(우리의 뉴럴 메모리)와 단기 메모리(어텐션)를 어떻게 결합할까?
트랜스포머 어텐션이 단기 메모리라면, 우리의 메모리는 장기 메모리가 됩니다.
다음 세 가지 변형(variant)을 제안합니다.

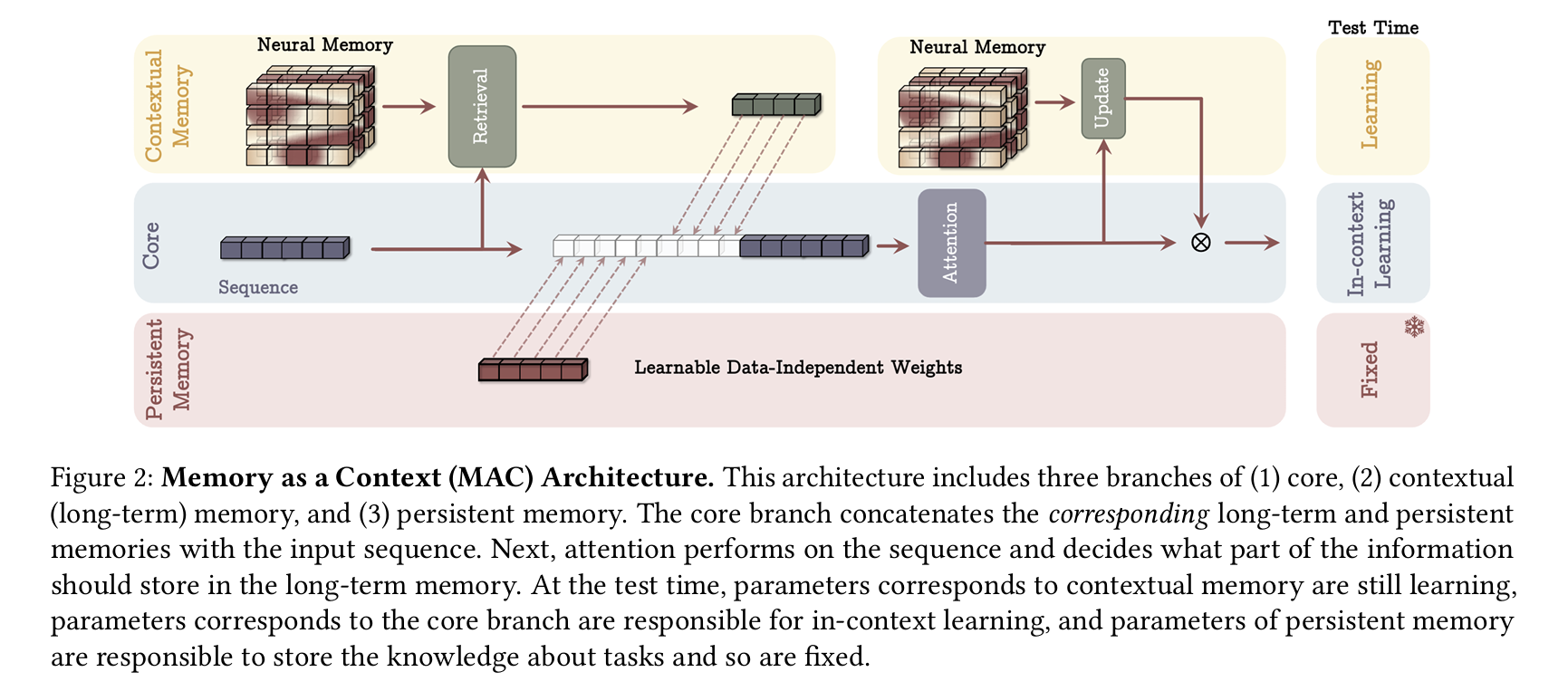
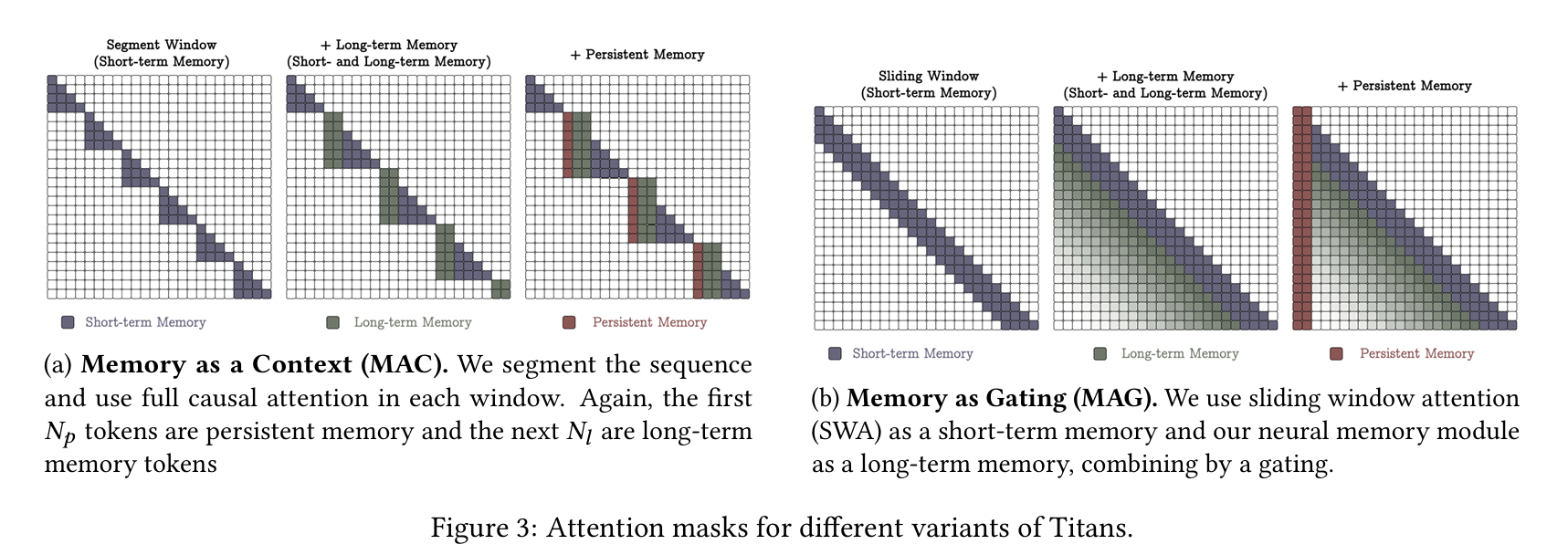
4.1 Memory as a Context (MAC)

시퀀스를 세그먼트 $S(i)$ 로 분할합니다.
시점 $t$ 세그먼트 $S(t)$ 가 들어올 때, 이미 학습된 $\mathcal{M}_{t-1}$ 을 조회해 과거 관련 정보를 얻습니다: $h_t = \mathcal{M}_{t-1}^*(\mathbf{q}_t), \quad \mathbf{q}_t = S(t)\,W^Q.$
영속적 메모리와 $h_t$ , 그리고 현재 세그먼트를 어텐션에 결합: $\tilde{S}(t) = [p_1,\ldots,p_{N_p}] \,\|\, h_t \,\|\, S(t), \quad y_t = \mathrm{Attn}(\tilde{S}(t)).$
이후 $y_t$ 를 통해 메모리를 업데이트하거나 최종 출력을 얻습니다.

장점:

어텐션이 필요할 때만 장기 메모리를 사용할 수 있음.
어텐션이 “세그먼트 중 어떤 정보가 메모리에 저장될지” 선별 가능.
테스트 시에 (i) 영속 메모리는 고정, (ii) 어텐션 파라미터는 인-컨텍스트, (iii) 뉴럴 메모리는 계속 학습 가능.

4.2 Gated Memory (MAG)

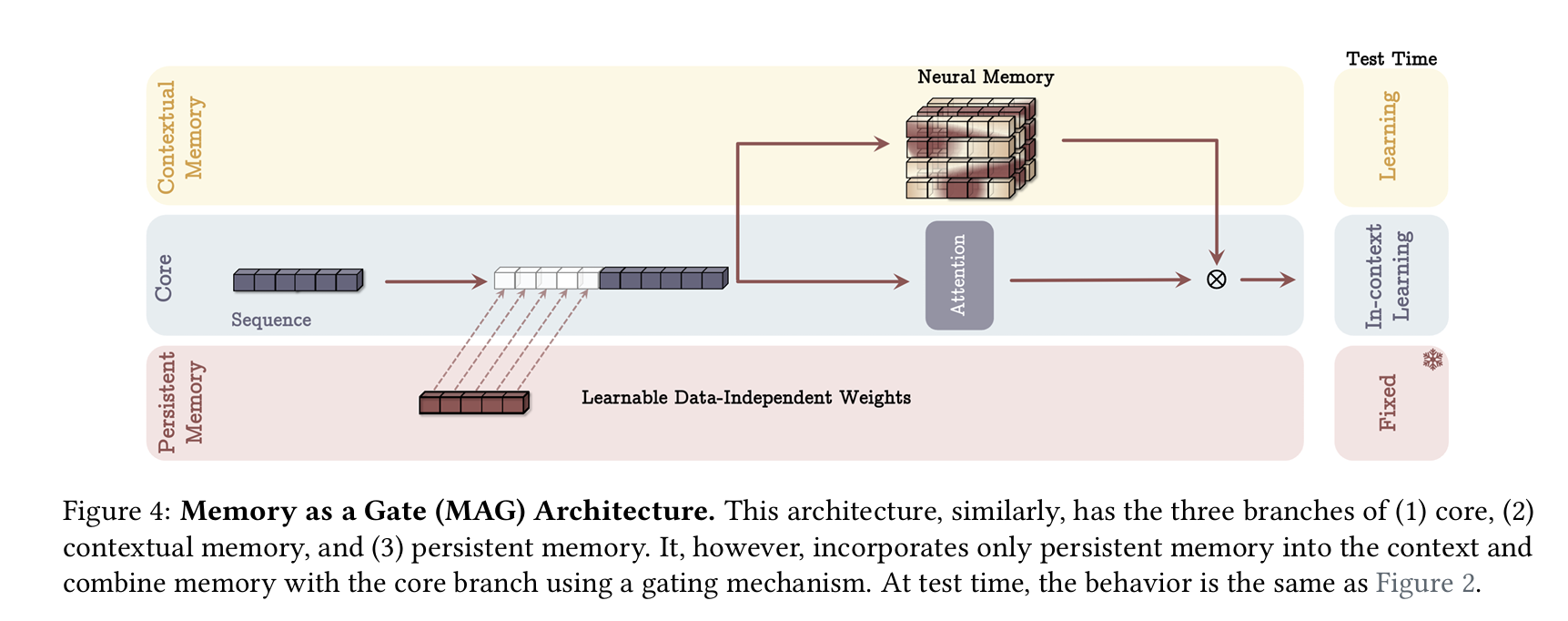
MAG 구조

한쪽 브랜치에서 입력 전체를 장기 메모리에 직접 입력해 업데이트,
다른 브랜치에서 슬라이딩 윈도우 어텐션(SWA)을 수행,
두 결과를 게이트( $\otimes$ )로 결합:

x_\text{new} = [p_1,\dots,p_{N_p}] \,\|\, x, \quad y = \mathrm{SW\text{-}Attn}^*(x_\text{new}), \quad o = y \,\otimes\, \mathcal{M}(x_\text{new}).

이 방식은 “정확한 단기 메모리(슬라이딩 창)”와 “장기 메모리”를 병렬로 두고, 최종 단계에서 게이트로 합칩니다.

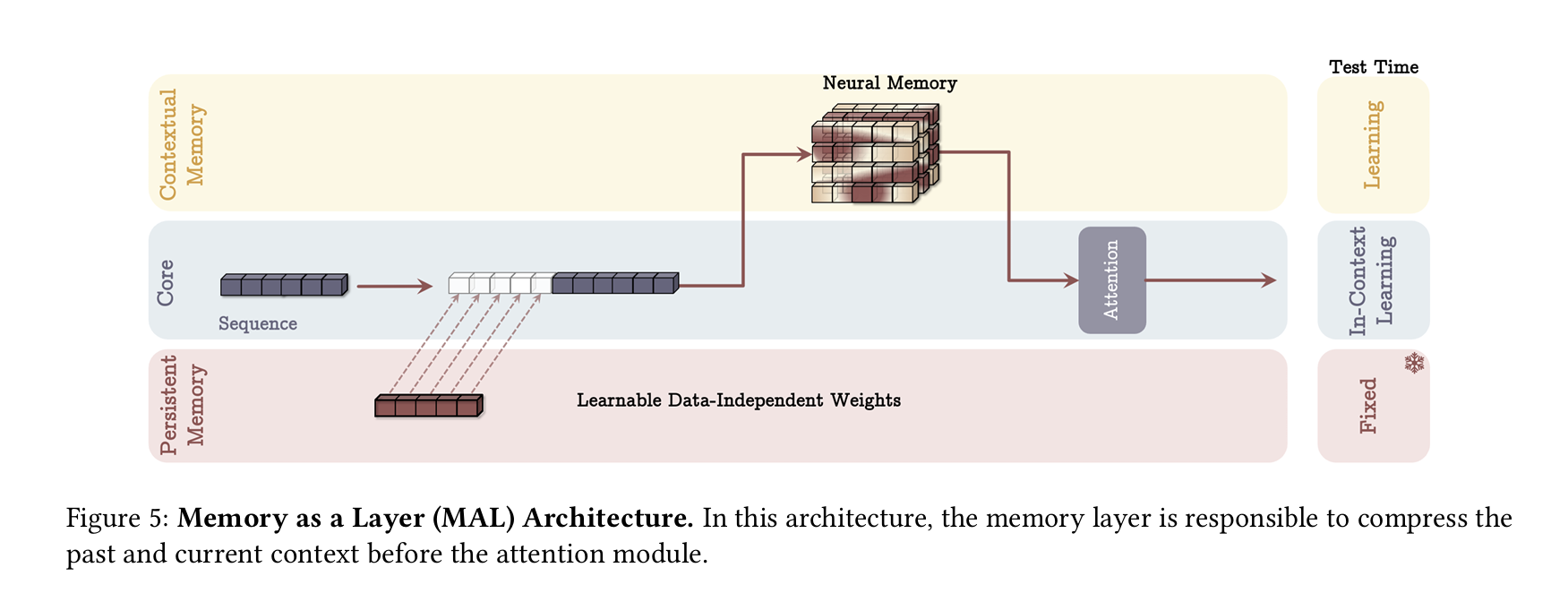
4.3 Memory as a Layer (MAL)

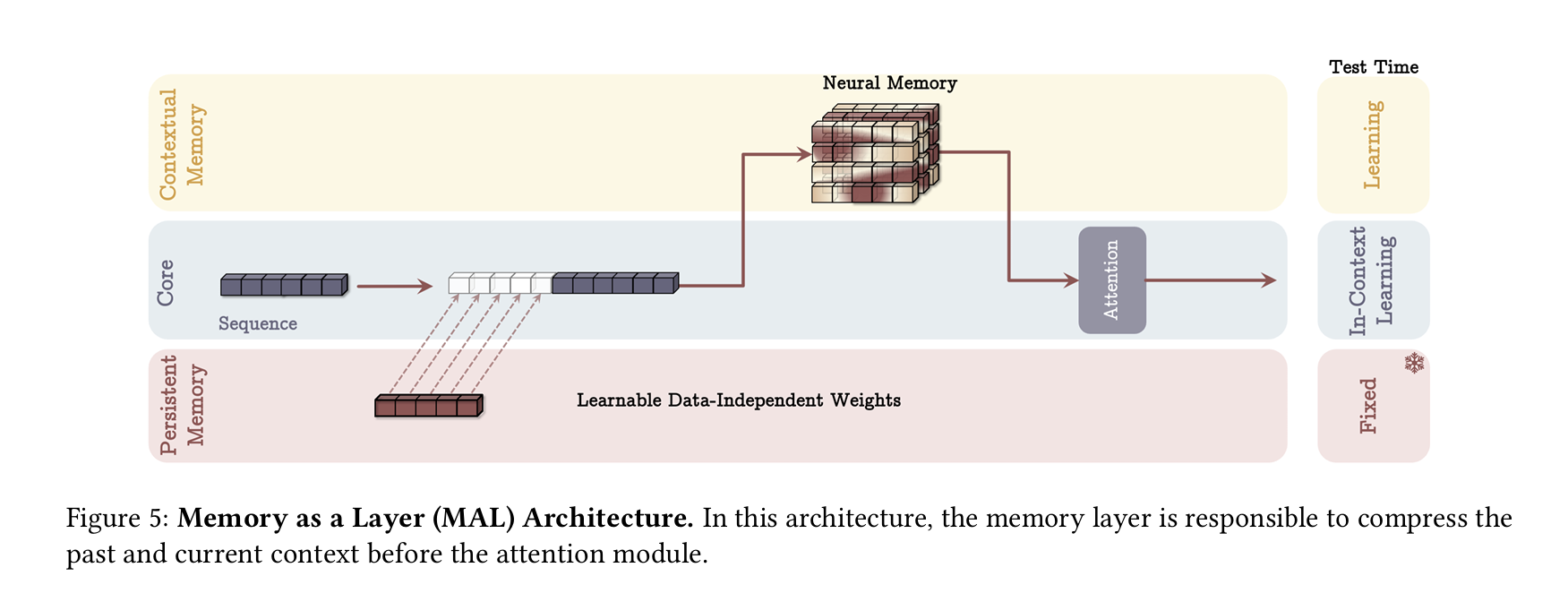
먼저 장기 메모리 레이어를 통과하여 $y = \mathcal{M}(x_\text{new}), \quad x_\text{new} = [p_1,\dots,p_{N_p}]\| x,$
그 뒤 SWA(또는 트랜스포머)에 넣어 $o = \mathrm{SW\text{-}Attn}(y).$ 이는 전형적인 “재귀 + 어텐션” 하이브리드 모델과 유사합니다.

메모리만 사용하는 경우

MAL 구조에서 어텐션을 제거하고 LMM(장기 메모리)만 사용하는 것도 가능합니다.
인간 두뇌의 여러 기억 체계가 독립적으로 기능할 수 있다는 비유와 일맥상통합니다.

4.4 Architectural Details

실제 구현에서는 잔차(residual), 정규화, 게이트 등을 모두 사용했습니다.
쿼리·키·값 계산 후 1D 컨볼루션(Depthwise-Separable)을 적용해 미세 성능을 개선했습니다.
게이트+정규화로 최종 출력을 조정했습니다.

Theorem 4.1.
트랜스포머, 대각선 선형 재귀 모델, 델타넷 등은 이론적으로 TC $_0$ 이하의 표현력을 갖는다고 알려져 있으나 [Merrill 2024], Titans는 TC $_0$ 를 넘어서는(state tracking 등) 문제까지 해결 가능해 더 높은 표현력을 갖습니다.

5 Experiments

이 절에서는 Titans(및 변형: LMM, MAC, MAG, MAL)을 언어 모델링, 상식추론, Needle-in-Haystack, 시계열 예측, DNA 모델링 등에 적용합니다.

5.1 Experimental Setup

모델:
- (1) LMM(장기 메모리 단독),
- (2) MAC,
- (3) MAG,
- (4) MAL.
- 각 170M, 340M, 400M, 760M 파라미터 버전을 실험.
비교 대상: Transformer++ [Touvron 2023], RetNet [Sun 2023], GLA [Yang 2024], Mamba [Gu 2024], Mamba2 [Dao 2024], DeltaNet [Yang 2024 Parallelizing], TTT [Sun 2024], Gated DeltaNet [Yang 2024 Gated], 하이브리드(Samba, Gated DeltaNet-H2) 등.
학습: Llama 2 토크나이저, 컨텍스트 길이 4K, AdamW(학습률 $4\times 10^{-4}$ , Cosine 스케줄, 배치 50만 토큰, weight decay 0.1) 등을 사용.

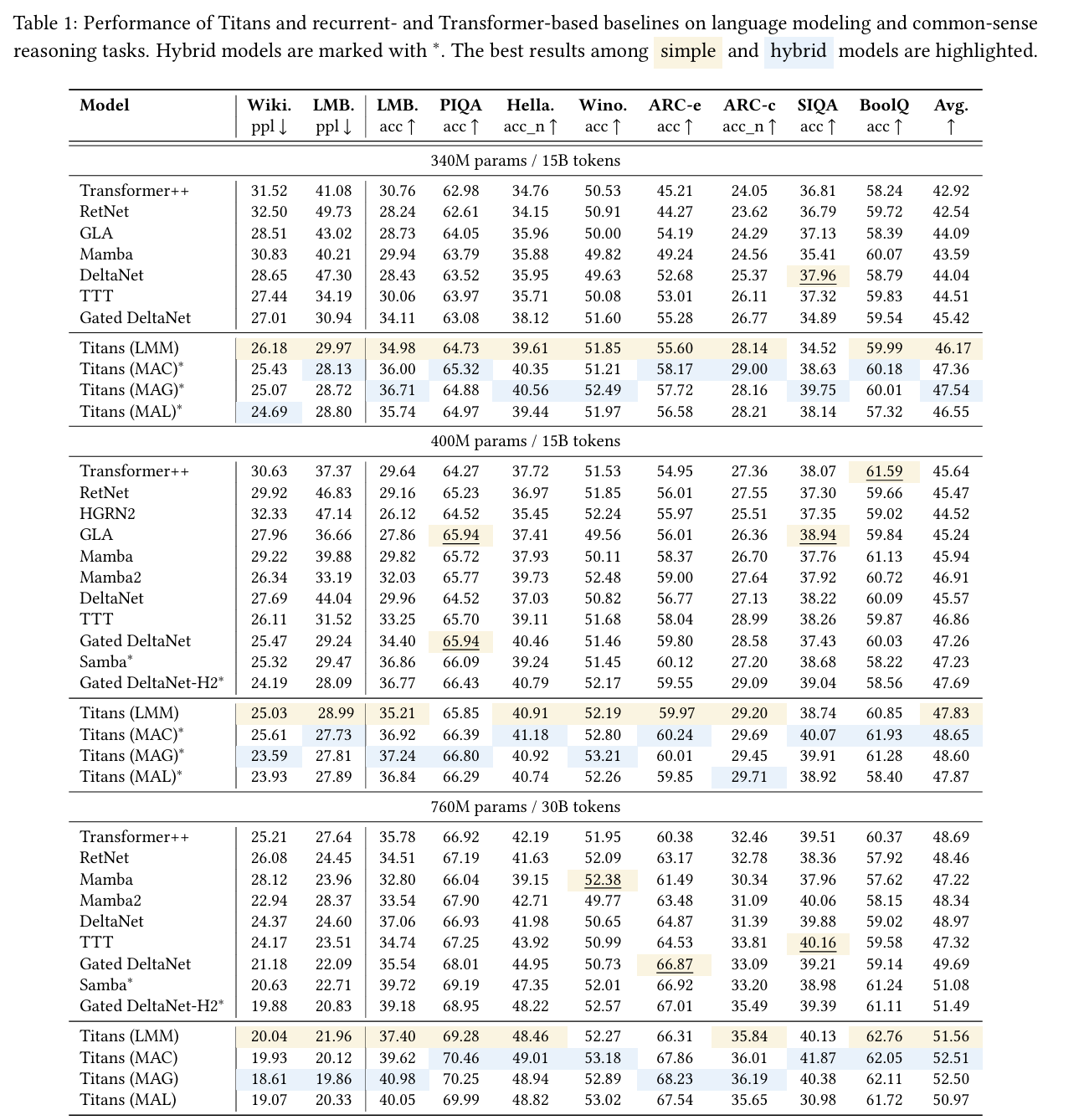
5.2 Language Modeling

아래 표는 언어 모델링(perplexity)과 상식추론 데이터셋 결과를 요약한 것입니다(340M, 400M, 760M 파라미터).

Model	Wikitext	LMB ppl	...	ARC-c	SIQA	BoolQ	Avg
Transformer++	31.52	41.08	...	24.05	36.81	58.24	42.92
RetNet	32.50	49.73	...	23.62	36.79	59.72	42.54
GLA	28.51	43.02	...	24.29	37.13	58.39	44.09
Mamba	30.83	40.21	...	24.56	35.41	60.07	43.59
DeltaNet	28.65	47.30	...	25.37	37.96	58.79	44.04
TTT	27.44	34.19	...	26.11	37.32	59.83	44.51
Gated DeltaNet	27.01	30.94	...	26.77	34.89	59.54	45.42
Titans (LMM)	26.18	29.97	...	28.14	34.52	59.99	46.17
Titans (MAC)	25.43	28.13	...	29.00	38.63	60.18	47.36
Titans (MAG)	25.07	28.72	...	28.16	39.75	60.01	47.54
Titans (MAL)	24.69	28.80	...	28.21	38.14	57.32	46.55

LMM vs. 기존 재귀 모델: TTT 등 대비 성능이 좋음. 모멘텀+망각 기제(게이트)로 메모리를 더 효율적으로 관리하는 효과로 추정.
Titans 하이브리드 vs. 기존 하이브리드: MAC, MAG, MAL 모두 타 모델(Samba, Gated DeltaNet-H2)보다 우수함.
MAC vs. MAG vs. MAL: MAC과 MAG가 유사한 성능, MAL은 약간 낮은 편(하지만 여전히 경쟁력 있음).

5.3 Needle in a Haystack

긴 문맥을 실제로 활용할 수 있는지 평가하는 대표 과제인 Needle-in-a-haystack(NIAH)을, RULER 벤치마크의 S-NIAH로 실험. 시퀀스 길이 2K, 4K, 8K, 16K에서 정답 비율을 측정한 결과:

LMM은 시퀀스 길이가 증가해도 높은 성공률을 유지.
MAC, MAG, MAL 역시 성능이 더 높음. MAC이 소폭 앞서는 경향.

5.4 BABILong Benchmark

더 복잡한 건초더미 과제인 BABILong [Kuratov et al. 2024]에서도 비교.

Few-shot: GPT-4, Llama3.1(8B) 등과 비교해도, 훨씬 적은 파라미터의 Titans(MAC)가 모두를 능가(그림 생략).
Fine-tuning: 소형 모델(RMT, Mamba 등)이나 초거대 모델(GPT-4, Qwen2.5-72B 등)과 비교해도 Titans(MAC)가 최고 성능. RMT처럼 작은 벡터로 메모리를 제한하는 방식보다 훨씬 유연함.

5.5 The Effect of Deep Memory

장기 메모리 계층 수( $L_\mathcal{M} = 1,2,3,4$ )에 따른 성능 변화를 살펴봄.

성능: 메모리 층이 깊어질수록, 긴 시퀀스에서 ppl이 현저히 낮아짐. 특히 파라미터 수가 작은 모델일 때 효과가 큼.
훈련 처리량: 계층 수가 증가하면(딥해지면) 훈련이 약간 느려지는 트레이드오프 존재.

5.6 Time Series Forecasting

자연어 외에도 시계열 예측 분야를 평가. Simba [Patro et al. 2024] 프레임워크에서 Mamba 대신 뉴럴 메모리를 사용해 ETT, ECL, Traffic, Weather 등 데이터를 실험.

전반적으로 기존 방법(Mamba, iTransformer, TimesNet 등)보다 낮은 MSE, MAE를 달성.

5.7 DNA Modeling

유전체(DNA) 분야인 GenomicsBenchmarks [Grevsova et al. 2023]에서도, LMM을 사전학습 후 다운스트림 분류 태스크에 적용.

Model	Enhancer Cohn	Enhancer Ens	...	Human OCR Ens.
CNN	69.5	68.9	...	68.0
DNABERT	74.0	85.7	...	75.1
GPT	70.5	83.5	...	73.0
HyenaDNA	74.2	89.2	...	80.9
Transformer++	73.4	89.5	...	79.5
Mamba	73.0	-	...	-
Neural Memory	75.2	89.6	...	79.9

전반적으로 경쟁력 있는 성능을 보임.

5.8 Efficiency

아래 그림(가상)에서, Titans와 베이스라인(트랜스포머, 다른 재귀 모델 등)의 훈련 처리량(tokens/sec)을 비교:

LMM은 Mamba2, GatedDeltaNet보다 약간 느림(커널 최적화 등에서 차이).
그러나 Titans(MAL 등)는 Flash-Attention 최적화 덕분에 매우 빠른 훈련 처리량.

5.9 Ablation Study

아래 표 예시:

Model	Language (ppl)	Reasoning	Long Context
LMM (base)	27.01	47.83	92.68
+Attn (MAC)	26.67	48.65	97.95
+Attn (MAG)	25.70	48.60	96.70
+Attn (MAL)	25.91	47.87	96.91
w/o Momentum	28.98	45.49	87.12
w/o Weight Decay	29.04	45.11	85.60
w/o Convolution	28.73	45.82	90.28
w/o Persistent Mem.	27.63	46.35	92.49

망각(가중감쇠), 모멘텀, 컨볼루션, 영속 메모리 등 모든 요소가 성능에 기여.
MAC과 MAG가 롱컨텍스트에서 우수하며, MAL은 상대적으로 단순해 훈련 속도가 빠르지만 성능은 조금 낮음.

6 Conclusion

본 논문에서는 “테스트 시점에서 데이터를 학습(암기)할 수 있는 뉴럴 장기 메모리”를 제안했습니다.

이 메모리는 모멘텀, 망각 게이트 등으로 놀람 이벤트를 효율적으로 관리하고, 딥(Deep) 구조로 더 높은 표현력을 확보합니다.
이를 전체 아키텍처에 통합하기 위해 Titans를 소개하고, 장기 메모리를 (1) 컨텍스트로, (2) 게이트로, (3) 레이어로 활용하는 세 가지 변형을 제시했습니다.
다양한 실험에서, Titans는 트랜스포머와 최신 선형 재귀 모델보다 뛰어난 장기 문맥 처리 능력을 보이며, 매우 긴 컨텍스트(2M 이상)에서도 높은 정확도를 달성했습니다.

Titans는 PyTorch와 JAX로 구현되었으며, 추후 학습 및 평가 코드를 공개할 예정입니다.

7 References

\printbibliography

(원문에 명시된 BibTeX/참고문헌 리스트)

Appendix

A.1 Linear Recurrent Models

트랜스포머의 $O(N^2)$ 문제를 해결하기 위해, 선형 재귀 모델들이 다시 주목받고 있습니다 [Tiezzi 2024].
1세대(예: RetNet, LRU, RWKV, S4/S5)는 데이터 독립적(decay) 방식을 사용하고,
2세대(예: Mamba, Griffin, RWKV6 등)는 게이트를 결합했으며,
3세대(예: DeltaNet, Gated DeltaNet, TTT, LongHorn)는 온라인 학습/메타러닝/델타 규칙을 도입해 메모리 갱신을 개선했습니다.
본 논문의 LMM은 (1) 모멘텀 기반 놀람, (2) 망각 게이트, (3) 딥 구조를 결합해 이들을 모두 일반화합니다.

A.2 Transformer-based Architectures

어텐션의 I/O 병목을 줄이는 FlashAttention, 스파스(sparse) 어텐션, 커널 기반(선형) 어텐션, 세그먼트 분할+작은 메모리(RMT, Memformer) 등이 제안되었습니다.
세그먼트 기반 메모리는 용량 한계나 잊힘 부재 등 문제점이 있어, MAC은 이를 대체할 수 있습니다.

A.3 Test Time Training and Fast Weight Programs

테스트 시 학습(local learning)은 과거부터 일부 분야에서 시도되어 왔습니다 [Zhang 2006, Mullapudi 2019].
Fast Weight Program [Schmidhuber 1992] 계열 연구는 키-값(연상) 메모리를 재귀적으로 업데이트하지만, 보통 순간 놀람에만 의존하거나 잊힘이 없다는 한계가 있습니다.
TTT 레이어[Sun 2024]와 비교 시, 본 연구의 LMM은 (1) 모멘텀 사용, (2) 망각 기제, (3) 딥 구조 가능 등의 차이가 있습니다.

끝.

코드짜는침팬지

학과 꼴찌 공대 호소인

이전 포스트