지금은 알고리즘 위주라서 알고리즘을 풀기 위한 개념 이해 + 문제 풀이로 구성되어 있다.

13일차

순열

for 중첩

• for를 중첩해서 순열을 구현하면 nPr에서 n은 랜덤이 가능하지만, r은 고정될 수 밖에 없다.

• 시간복잡도 : 중복순열(nTTr) -> n^r

순열	중복순열

재귀로 푸는 방법

• 초기화: P(0) or P(r-1) 상관이 없다 (bottom -> up인지 top -> down인지를 결정하는 것이기 때문)

• 기저(중단) 조건

  • 0 ~ r-1 까지 (0 < r)

  • r~1 ~ 0 까지 (r-1 > -1)

• 시간 복잡도가 오래 걸릴 때는 공간 복잡도로 해결할 수 있다.

boolean[] visited

visited 배열을 생성해서 기본값으로 false (사용 x, 중복 x)를 둔 뒤, true (사용 O, 중복 O)가 되면 visited 배열에 저장한다.

이렇게 되면 시간복잡도가 r^2에서 1로 바뀐다. (-> boolean 배열이 true / false 중 어느 것인지 확인만 하면 되니까)

=> 시간복잡도는 n^(r-중복제거) 가 된다

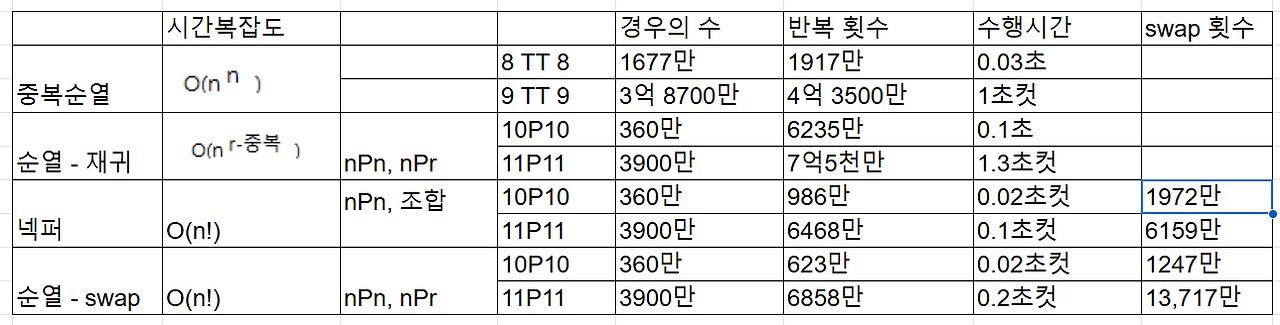
따라서 순열의 시간복잡도 한계치는 아래와 같다.

순열 시간복잡도 한계치

- 일반재귀 : 9P9
- swap, n, p : 10P10
- DP : 11P11 이상

• 시간복잡도 총 정리
  

---

순열과 관련된 문제

SWEA 6808 규영이와 인영이

1~18까지의 합 최대 총합 171

⇒ 86+86정도이기 때문에 무승부는 사실상 없음

- 두 카드의 총합은 (18*19)/2 = 171이므로 무승부는 나오지 않음. 이기거나 지는 상황만 체크한다.
- 입력
    - 규영이의 카드가 입력으로 들어오고, 순서는 고정
    - 인영이의 카드를 규영이가 선택하지 않는 카드로 선택한다.
        - 18개 카드 중 규영이 카드 빼고 선택해야 함
            - 규영이 카드를 입력 받으면 boolean 배열에 규영이 카드 기록 (카드번호가 index)
            - boolean의 false인 index를 인영이의 카드로 사용하기
- 순열 만들기
    - 순열을 다 만든 후에 반복문을 통해 전체 카드에 대한 승패를 결정
 

---

비트마스크

• 정수의 이진수 표현을 자료구조로 활용하여, 각 비트의 상태를 통해 집합이나 여러 상태를 효율적으로 표현하고 처리하는 기법

• 비트연산자 : &, |, shift, XOR

• 0 양수 / 1 음수 로 이루어져 있다.

비트마스크를 구하는 방법 (2, 3번 중요!!)

1. 공집합과 꽉 찬 집합 구하기
 	* A = 0;			//32개의 원소가 모두 0이므로 공집합
 	* n = 10; 			//10개인 원소 (1111111111)
 	* A = (1<<n)-1;		//꽉 찬 집합
 	
    0000000001 << 10 ==>10000000000 
    10000000000 -1 = 1111111111  
    
2. 특정 위치에 1이 있는지 check로 & 사용 
 	*  &, and  : 연산하려는 두 비트가 모두 1일때 1이고 나머지는 0
                 특정 위치에 1이 있는지 체크 용도로 사용,  data & 0 => 0으로 초기화   
                 
    int a1 = 0b1000;
    int b1 = 0b0010;
    int c1 = 0b1110;
    
3. 원소 추가 : k번째 위치에 원소를 추가(1로 마스킹)하기 
	* A |= (1<<k)
    * k번째는 뒤에서 부터 세기 (0번째 부터~)
    
    c1 |= (1<<k);
    System.out.println(Integer.toBinaryString(c1));

---

SWAP 순열

• 원소의 위치를 바꿔가면서 새로운 순열을 만들어주는 것이다

• 시간을 많이 단축할 수 있다 (n!)

1. depth ~ R-1 까지 swap을 반복한다 (for문)
2. depth 전 index는 고정이다 (확정)
   2-1. 기존의 원소 위치만 교체하므로 중복 검사를 할 필요가 없다.

⇒ depth=R까지 반복

특징

• 배열의 첫 원소의 위치부터 순서대로 하나씩 바꾸며 모든 값을 한번씩 swap 한다.

• depth를 기준 인덱스로 하여 depth 보다 인덱스가 작은 값들은 그대로 고정하고 depth 이상의 인덱스들만 swap을 진행한다.

• 순열을 따로 구하지 않아도 된다 -> 원본 배열을 그대로 사용한다

• nPn, nPr 모두 됨. 단 nPr시 전체 배열에서 앞에 r개만 사용

• 단점: 순열이 사전순(오름차순)으로 나오지 않는다. 수행속도 9P9 8ms 안전 10P10 34ms 안전

만약 R = 3인 경우)

• R ≥ 3 일 때는 마지막은 결국 자기 자신 교체이기 때문에 depth = R까지 갈 필요 없음 (R-1까지만 가면 된다)
• R ≤ 2 일 때는 depth = R까진 가야 됨

public static void main(String[] args) {
    input = new int[] {1,2,3};
    N = input.length;
    R = input.length;

    long start = System.currentTimeMillis();		
    permutation(0); // 0번째 원소부터 뽑기
    long end = System.currentTimeMillis();
    System.out.printf("순열 수: %d   반복횟수:%d    수행시간: %dms %n ", tc, count, end-start);
		
 	}
	// swap 함수
	private static void swap (int i, int j) {
		int temp = input[i];
		input[i] = input[j];
		input[j] = temp;
	}
	
	/**
	 * @param depth : 순열 배열의 index
	 **/
	private static void permutation(int depth) {

	if (depth==R){
		tc++;
		return;
	}
	
	// depth 이전 인덱스는 고정, depth부터 swap 하기 
	for (int i = depth; i < N; i++) { // i = depth이고, i = 0이 아니기 때문에, depth부터 하기 때문에 시간이 빠름!!!!!
		count++;	// 반복 횟수 세기
		
		// 두 수를 swap해서 새로운 순열을 만든다.
		swap(i, depth);
		permutation(depth+1);
		
//		 다음 순열을 만들기 위해서 원복
		swap(i, depth);	// 이렇게 해도 바뀜
//		swap(depth, i);
	}
}

---

조합

• 서로 다른 N개의 원소에서 R개를 중복없이, 순서를 고려하지 않고 선택하는 것 (ex. 로또 뽑기)

• 특징: 첫번째 인덱스 숫자 < 두번째 인덱스 숫자 < … < n번째 인덱스 숫자
  -> 항상 첫 < 둘 이렇게 숫자가 더 커짐
  => 중복 없이, 순서를 고려하지 않기 때문에 조합의 특징이 뒤에 있는 원소의 index는 항상 앞에 있는 원소의 index 보다 커야된다.

package combination;

import java.util.Arrays;


public class CombinationTest1 {
	static int tc; // test case
	static int n, r;
	static int[] numbers;
	static int[] input;
	
	public static void main(String[] args) {
		input = new int[] {1,2,3};
		n = input.length;
		r = 2;
		numbers = new int[r];
		
		combi(0,0);
	}

	/**
	 * @param depth		조합을 뽑아놓은 배열의 index
	 * @param start		조합을 시작할 index
	 * */
	private static void combi(int depth, int start) {
		if (depth == r) { // 기저조건
			tc++;
			return;
		}
		for (int i = start; i < n; i++) { // 반복조건
			numbers[depth] = input[i];
			combi(depth+1, i+1);
			
		}
	}

}

+ 조합 관련 문제

• 백준 2309 일곱난쟁이 (해결)

package 코드공유.BOJ;

import java.util.Arrays;
import java.util.Scanner;

public class Main_2309_일곱_난쟁이_김주희 {
	static int n, r;
	static int[] numbers;
	static int[] input;
	static int total;
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		
		input = new int[9];
		n = input.length;
		r = 7;
		numbers = new int[r];
		
		
		for (int i=0; i < n; i++) {
			input[i] = sc.nextInt();
		}	
		combi(0,0);
	}

	private static void combi(int depth, int start) {
		if (depth == r) {
			if (total == 100) {
				Arrays.sort(numbers);
				
				for (int num : numbers) {
					System.out.println(num);
				}
				System.exit(0);
			}
			return;
		}
		
		
		for (int i=start; i < n; i++) {
			numbers[depth] = input[i];
			total += input[i];
			combi(depth+1, i+1);
			total -= input[i];
		}
		
	}
}
 

---

14일차

문제 푸는 데 집중해서 기록해둔게 없다... 아마 조합 문제를 엄청 고민했던 것 같다 ㅜ

공포의 수영장 ..

이후 프론트 대면반 단체 회식이 있어서 대면반 사람들과 친해지게 된 계기가 되어서 너무 좋았고 알찼던 시간이었다.

프로젝트 때문에 맘 편히 즐기진 못했지만 .. ㅜㅡㅜ

---

15일차

알고리즘 고수가 되면 풀어 볼 문제

1. 백준 1062 가르침 (비트마스킹)

2. 프로그래머스 42820 후보키

자료구조

선형

• 데이터와 다음 데이터가 연결된 것 (1개씩 맵핑된다)

스택

• 먼저 들어간 값이 가장 나중에 나오는 구조 (LIFO)

• 주로 괄호 검사기 문제에 주로 활용된다.

큐

• 먼저 들어간 값이 가장 먼저 나오는 구조 (FIFO)

• 요세푸스 문제가 큐 문제이다.

---

관련 문제

백준 10799 쇠막대기 (stack)

• 괄호 짝이 맞으면 레이저를 쏴서 현재 레이저를 쐈을 때 앞에 짝이 안 지어진 '('의 갯수를 세는 문제이다.

• 현재 괄호 바로 전 괄호의 모양에 따라서 pop을 할 지, total에 값이 쌓이게 될 지 결정된다.

• 문제를 해석하는 데 정말 오래 걸렸다.. 그래도 해석만 하면 어느 정도 풀리는 문제였다.

package 코드공유.BOJ;

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Stack;

public class Main_10799_쇠막대기 {

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader (new InputStreamReader(System.in));
		String line = br.readLine();
		int total = 0;
		
		Stack<Character> stack = new Stack<>();
		
		for (int i = 0; i < line.length(); i++) {
			char c = line.charAt(i);
			if (c == '(') {
				stack.push(c);
			} else if (c == ')') {
				stack.pop();
				
				if (line.charAt(i - 1) == '(') {
				total += stack.size();
				} else {
					total++;
				}
			} 
		}	
		System.out.println(total);
	}
}

백준 1158 요세푸스 문제 (queue)

• 문제 자체는 쉬웠지만, 풀기 어려웠던 문제

• K번째 해당하는 숫자를 poll() 하고 그 값을 offer()를 통해 queue 뒤로 삽입한 뒤, poll()한 값을 result 리스트에 담아서 결과를 출력하는 문제이다.

• 출력 방식 자체도 독특했다.

package 코드공유.BOJ;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Scanner;

public class Main_1158_요세푸스_문제 {
	int N;
	int K;
	
	public static void main(String[] args) throws Exception {
		Scanner sc = new Scanner(System.in);
		int N = sc.nextInt();
		int K = sc.nextInt();
		
		Queue<Integer> q1 = new LinkedList<>();
		
		for (int i = 1; i <= N; i++) {
			q1.offer(i);
		}
		
		List<Integer> result = new ArrayList<>();
		
		while(!q1.isEmpty()) {
			for (int j = 0; j < K-1; j++) {
				int var = q1.poll();
				q1.offer(var);
			}
			result.add(q1.poll());
		}
		
		System.out.print("<");
		for (int i = 0; i < result.size(); i++) {
			System.out.print(result.get(i));
			if (i != result.size() - 1) {
				System.out.print(", ");
			}
		}
		System.out.print(">");

	}
}
 

---

회고

드디어 순조부가 끝났나?? 싶긴 한데.. 문제들이 너무 어렵고 헷갈려서 하염없이 문제만 쳐다봤던 날이 많아서 아쉬운 것 같다.

프로젝트가 생각보다 늦게 끝나고 너무 빠듯해서 주말에도 알고리즘 공부할 시간이 없었어서 너무 아쉬웠다 ㅜㅜ

얼른 백엔드 파트 전에는 끝내서 백엔드 때는 진도에 맞춰서 잘 따라갈 수 있도록 해야겠다.

하~~ 지긋지긋한 프로젝트 빨리 끝내고 싶다 이번주 내로 끝내버려야지 .......... 아마도....

사실 이번 프로젝트하면서 백엔드 공부의 중요성을 약간 깨닫게 되어서 빨리 알고리즘 끝내고 백엔드 배워 보고 싶긴 하다

그리고 이번 주 개꿀인 점 : 하루 휴강 🥳🥳🥳🥳🥳

그리고 너무 기대된다 !!!!! 새로운 지식 많이 얻을 것 같다