프로그래머스]DFS/BFS 타겟넘버 (Java)

https://school.programmers.co.kr/learn/courses/30/lessons/43165

class Solution {
    int[] numbers;
    int target;
    int answer;
    public int solution(int[] numbers, int target) {
        answer = 0;
        this.numbers = numbers;
        this.target = target;
        dfs(0,0);
        return answer;
    }
    
    public void dfs(int index, int sum) {

		//종료 조건
		if(index == numbers.length){ //배열을 다 탐색했고
			if(sum == target)answer++; //target이 결과와 같을때는 종료 
			return;
		}
        
		//실행 코드 재귀함수 
		dfs(index+1, sum+numbers[index]);

		dfs(index+1, sum-numbers[index]);

	}
}

이 문제는 이진트리로 자료를 생각하며 풀면 조금 이해가 간다.

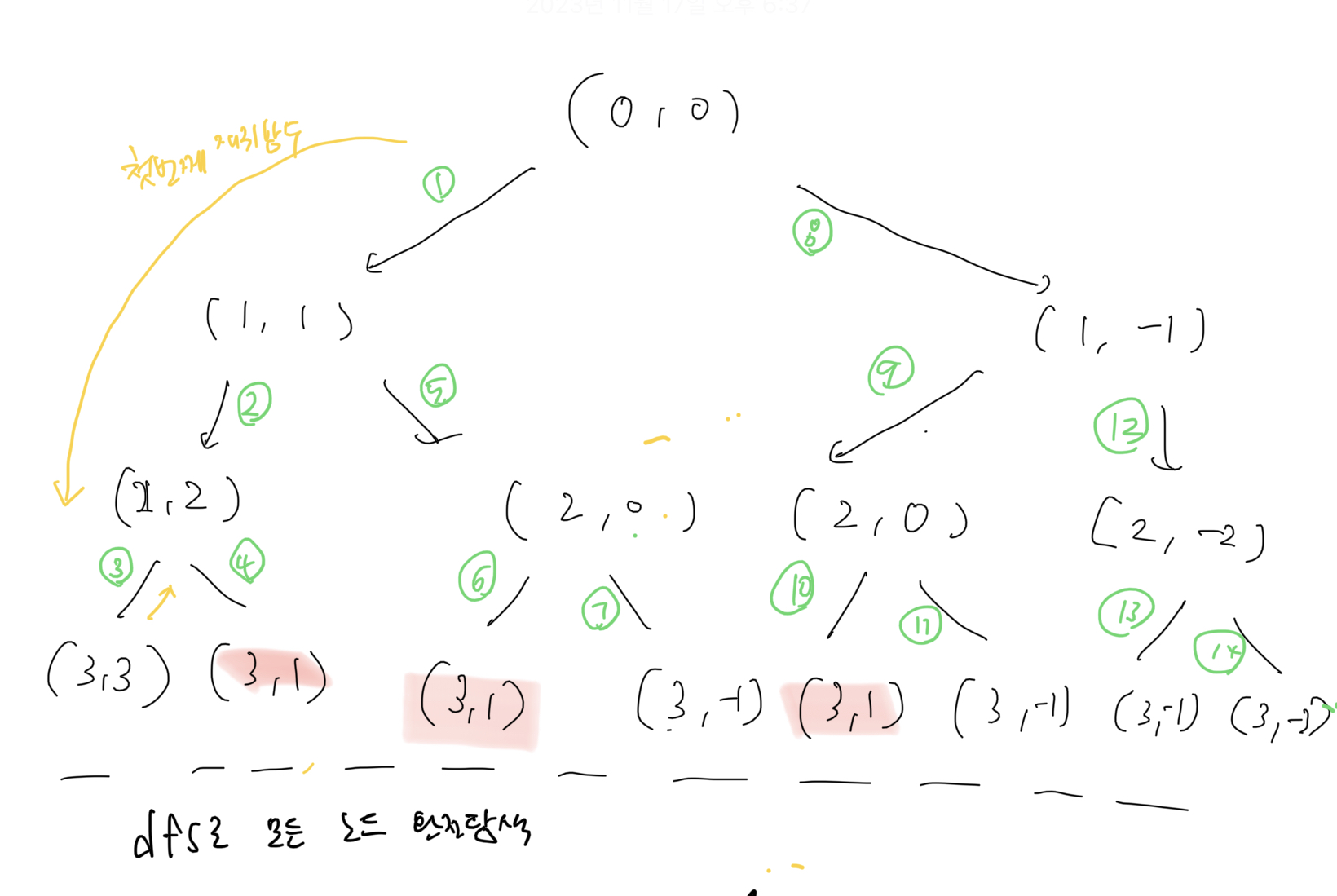
완전탐색(dfs)으로 모든 배열에 있는 수를 더하거나 빼면서 결과값이 맞는지 아닌지 찾으면 된다.

dfs함수에서 index와 sum 값을 받는데,

index는 numbers의 배열을 탐색하기 위한 수이고

sum은 number을 더하거나 빼면서 담기위한 수이다.

위의 이진트리는 [1,1,1]가 numbers로 주어졌을때 그리고 target을 1로 놓았을때를 가정한 이진트리다.(빨간색으로 형광펜을 친 3개가 답으로 return된다.)

		dfs(index+1, sum+numbers[index]);
		dfs(index+1, sum-numbers[index]); 

이 두개의 재귀함수는 이진트리의 구조를 탐색하게 되어있다.

간단하게 설명하자면 그래프에서 오른쪽에 해당하는 탐색은 첫번째 재귀함수가

왼쪽에 해당하는 탐색은 두번째 재귀함수가 돌게 된다.

위의 코드가 스택에 쌓일때 이렇게 된다 .

스택 초기 상태: []

1. dfs(0, 0) 호출
   스택: [dfs(0, 0)]

2. dfs(1, 1) 호출 (0번째 숫자를 더하는 경우)
   스택: [dfs(0, 0), dfs(1, 1)]

3. dfs(2, 2) 호출 (1번째 숫자를 더하는 경우)
   스택: [dfs(0, 0), dfs(1, 1), dfs(2, 2)]

4. dfs(3, 3) 호출 (2번째 숫자를 더하는 경우)
   스택: [dfs(0, 0), dfs(1, 1), dfs(2, 2), dfs(3, 3)]

5. dfs(3, 3) 처리 후 반환 (기저 조건에 도달)
   스택: [dfs(0, 0), dfs(1, 1), dfs(2, 2)]

6. dfs(3, 1) 호출 (2번째 숫자를 빼는 경우)
   스택: [dfs(0, 0), dfs(1, 1), dfs(2, 2), dfs(3, 1)]

7. dfs(3, 1) 처리 후 반환 (기저 조건에 도달, target과 일치하는지 확인)
   스택: [dfs(0, 0), dfs(1, 1), dfs(2, 2)]

8. dfs(2, 2) 처리 후 반환
   스택: [dfs(0, 0), dfs(1, 1)]

9. dfs(2, 0) 호출 (1번째 숫자를 빼는 경우)
   스택: [dfs(0, 0), dfs(1, 1), dfs(2, 0)]

10. dfs(3, 1) 호출 (2번째 숫자를 더하는 경우)
    스택: [dfs(0, 0), dfs(1, 1), dfs(2, 0), dfs(3, 1)]

11. dfs(3, 1) 처리 후 반환 (기저 조건에 도달, target과 일치하는지 확인)
    스택: [dfs(0, 0), dfs(1, 1), dfs(2, 0)]

12. dfs(3, -1) 호출 (2번째 숫자를 빼는 경우)
    스택: [dfs(0, 0), dfs(1, 1), dfs(2, 0), dfs(3, -1)]

13. dfs(3, -1) 처리 후 반환 (기저 조건에 도달)
    스택: [dfs(0, 0), dfs(1, 1), dfs(2, 0)]

14. dfs(2, 0) 처리 후 반환
    스택: [dfs(0, 0), dfs(1, 1)]

15. dfs(1, 1) 처리 후 반환
    스택: [dfs(0, 0)]

16. dfs(1, -1) 호출 (0번째 숫자를 빼는 경우)
    스택: [dfs(0, 0), dfs(1, -1)]

17. (위와 같은 과정 반복, 2번째, 3번째 숫자에 대해 더하기/빼기 연산 수행)

18. dfs(0, 0) 처리 후 반환
    스택: []

후기

dfs가 익숙치 않고 재귀에 대한 개념이 약하다 보니 고생했다.

그래서 1. 재귀가 어떻게 돌아가는지(어떻게 스택에 쌓이는지)

1. 이진트리로 가시화해보기

해보니 문제는 쉽게 풀렸다 .