N-Queens Algorithm Review

알고리즘 개요

N-Queens는 체스의 Queens의 특성을 이용하여 백트래킹 개념을 학습하는데 이용되는 대표적인 알고리즘이다.

문제의 목표는 n * n 크기의 체스판에서 각각의 Queen이 서로를 공격하지 않는 위치에 말을 위치시키는 것이다.

이러한 Queen의 특성을 이용하여 풀어야할 문제는 다음 두 가지다.
1. 특정 위치에 Queen을 놓았을 때 올바른 솔루션을 찾는 함수의 작성
2. 어떠한 사이즈의 체스판이던 Queen을 놓을 수 있는 모든 경우의 수를 찾는 함수의 작성

체스에서의 Queen의 특성

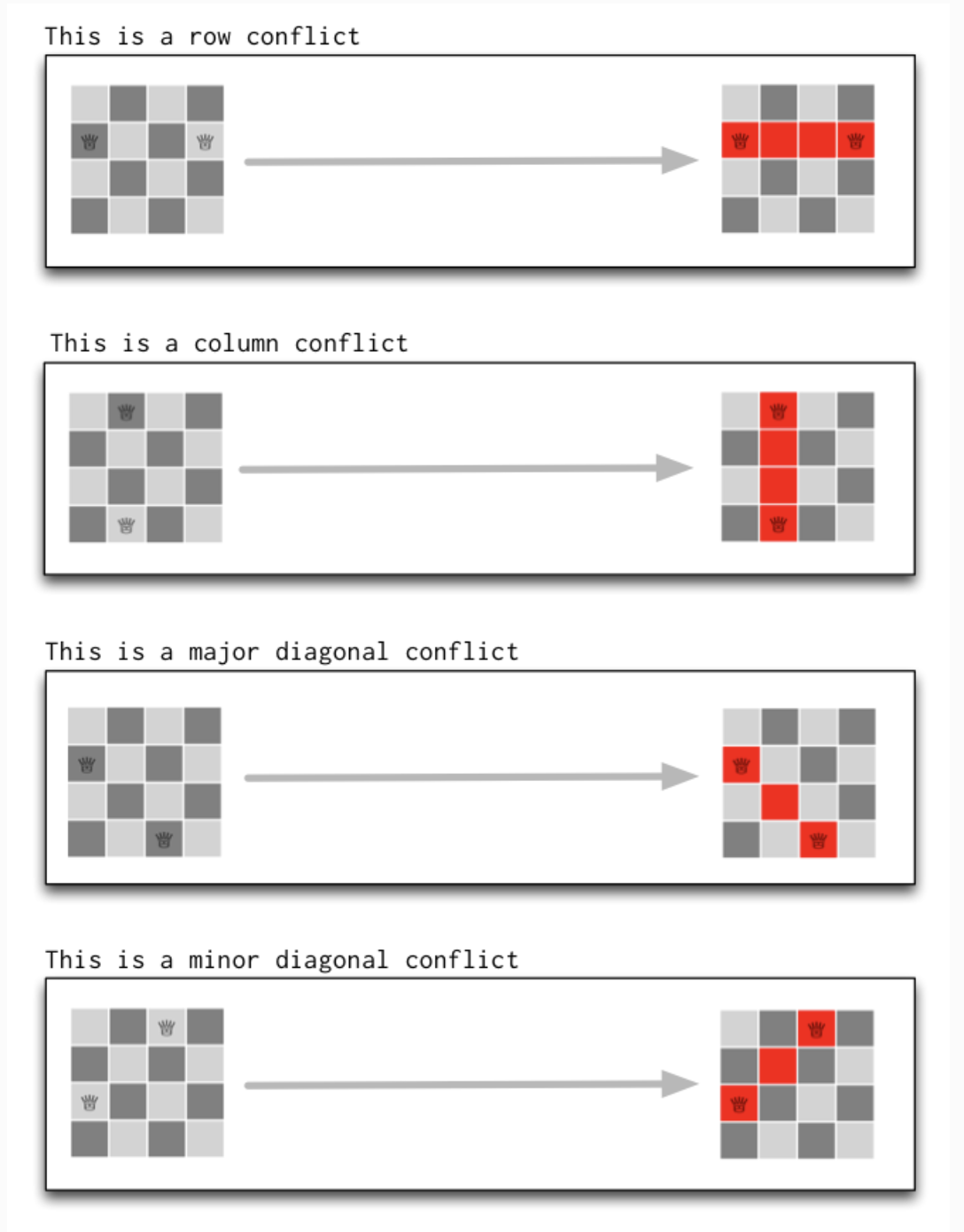
퀸(Queen→왕비/여왕)은 체스의 기물들 중 하나로, 가장 가치 있는 기물로 평가된다. 비숍과 룩을 합쳐 놓은 이동을 할 수 있어서, 오와 열을 따라 이동하는 것은 물론 대각선으로도 이동할 수 있다.

참고할 개념

• 백트랙킹(Backtracking): 백트랙킹은 N-Queens 문제처럼 여러개의 솔루션을 가진 문제에서 모든 방법을 탐색하는 것이다. 대표적인 완전 탐색 방법으로는 DFS(깊이 우선 탐색)이 있다.

DFS는 재귀 호출을 이용해서 탐색할 수 있으며, depth가 깊더라도 탐색할 수 있다는 장점이 있다. 하지만 굳이 목표가 있지 않는 경로까지 탐색하는 것은 비효율적이다. 그래서 고안된 것이 백트래킹으로 DFS에서 더 이상 유망하지 않은 탐색경로를 배제하여 비효율적인 탐색을 줄일 수 있다.

구현해야 할 함수

• makeEmptyMatrix(n): n*n의 체스판(행열)을 만듦
• togglePiece(row, col): 인자로 들어오는 값을 체스판의 행과 열에 위치에 위치 또는 제거함
• hasAnyQueenConflictsOn(row, col): 인자로 주어진 위치에 퀸을 놓았을 때, 충돌이 있는지 true/false로 반환함
• hasNcountMal: 체스판에 몇 개의 Queen이 있는지 체크함
• diagnoalArr: 퀸의 진행방향의 충돌을 체크하여 유망성을 체크하는 함수

문제의 접근법과 자바스크립트 코드

Find N-Queens Solution: 임의의 위치에 퀸을 놓았을 때 솔루션을 찾는 문제
1. 인자로 주어진 n으로 n*n의 체스판(행열)을 만든다.
2. 재귀함수를 이용하여 만들어진 체스판에 퀸을 위치시키고 충돌테스트를 한다.
3. 충돌한다면, 위치시킨 퀸을 빼고, 다음 열에 퀸을 위치시킨다.
4. 열의 끝까지 가면 체스판에 모든 퀸이 위치되었는지 확인하고, 아니라면, 다음 행에 2~3 반복한다.

window.findNQueensSolution = function (n) {
  let solution = new Board(makeEmptyMatrix(n));

  function recursion(row, col) {
    solution.togglePiece(row, col);
    if (solution.hasAnyQueenConflictsOn(row, col)) {
      solution.togglePiece(row, col);
      return recursion(row, col + 1);
    } else if (solution.hasNcountMal() !== n) {
      return recursion(row + 1, 0);
    } else {
      return solution;
    }
  }

// 예외처리
  if (n === 0) {
    return [];
  } else if (n === 1) {
    return [[1]];
  } else if (n === 2) {
    return makeEmptyMatrix(2);
  } else if (n === 3) {
    return makeEmptyMatrix(3);
  }

  solution = recursion(0, 1);
  return solution.rows();
};

Count NQueens Solutions: n*n의 체스판이 주어질 때, 가능한 모든 솔루션의 수를 찾는 문제

• 트리구조와 재귀함수를 이용하여 유망성 체크 후 모든 가능한 경우의 수를 만드는게 핵심

1. 첫 번째 행을 기준으로 해서 n만큼 노드(루트)를 만들어 배열에 담는다.
2. 재귀함수를 이용하여 마지막 depth까지 각각의 루트를 유망성을 확인하여 가능한 모든 경우의 수의 노드를 만든다.
3. depth가 n과 같은 경우(유망성 확인을 끝내고 완성된 솔루션이 되는 경우)가 나오면 count를 1씩 증가시킨다.
4. count를 반환시킨다.

window.countNQueensSolutions = function (n) {

// 예외처리
  if (n === 0 || n === 1) {
    return 1;
  }
  if (n === 2 || n === 3) {
    return 0;
  }

  let storage = [];
  let solutionCount = 0;

  const Tree = function (row, col) {
    this.row = row;
    this.col = col;
    this.children = [];
  };

  Tree.prototype.addChild = function (value) {
    let newTree = Tree(value);
    this.children.push(newTree);
  };

// 유망성 체크 함수
  function diagnoalArr(arr, row, col) {
    for (let i = 0; i < arr.length; i++) {
      if (arr[i][0] === row || arr[i][1] === col ||
        Math.abs(arr[i][0] - row) === Math.abs(arr[i][1] - col)) {
        return false;
      }
    }
    return true;
  }


  for (let rt = 0; rt < n; rt++) {
    let colrowArr = [];
    let root = new Tree(0, rt);
    colrowArr.push([0, rt]);
    function recursion(tree, rowIndex) {
      if (rowIndex === n) {
        solutionCount++;
        return;
      }
      for (let i = 0; i < n; i++) {
        if (diagnoalArr(colrowArr, rowIndex, i)) {
          let newTree = new Tree(rowIndex, i);
          colrowArr.push([rowIndex, i]);
          recursion(newTree, rowIndex + 1);
          colrowArr.pop();
          tree.children.push(newTree);
        }
      }
    }
    recursion(root, 1);

    storage.push(root);
  }
  return solutionCount;
};