
강의 출처
이 링크를 통해 구매하시면 제가 수익을 받을 수 있어요. 🤗
그림으로 쉽게 배우는 자료구조와 알고리즘 (기본편)
인프런 강의 - 그림으로 쉽게 배우는 자료구조와 알고리즘 (심화편)
인프런 강의 - 만들면서 쉽게 배우는 컴퓨터 구조
개요
이번시간엔 불 대수라는 개념에 대해 다뤄보았다.
-
" 조지 불 " 이라는 사람이 책을 발표했는데,논리학과 대수학을 연결시킨 획기적인 업적 -> 그러나 실용적인 응용방안이 없음
-
" 클로드 섀넌 " 이 전기 스위치로 불대수의 사칙 연산이 가능하다는 것을 증명 -> 즉, 전기 스위치(=디지털 장치)는 불 대수를 기반으로 작동함.
그래서 불대수가 뭔데요?
-
일반 대수학과는 달리, 변수가 0과1 또는 거짓과 참으로만 표현되는 두가지의 논리변수를 사용함.
-
이러한 두가지 상태만으로도 모든 계산이 가능하다는 걸 클로드 섀넌이 밝힘.
-
0과 1로 표현되는 모든 영역에서 활용된다 ( 오늘날 컴퓨터(디지털)회로 설계에서 많이 사용되고, 이전에는 전기스위치로 변수를 표현하였으나, 오늘날에는 트랜지스터로 변수 표현함 )
목차
- 불 연산
- 불 대수의 성질과 법칙
- 불 함수
- 진리표를 변환하는 방법
1️⃣불 연산
- 논리 연산 : 0과 1 두가지 값 만으로 다룸 => 이걸 불 연산이라고도 부름
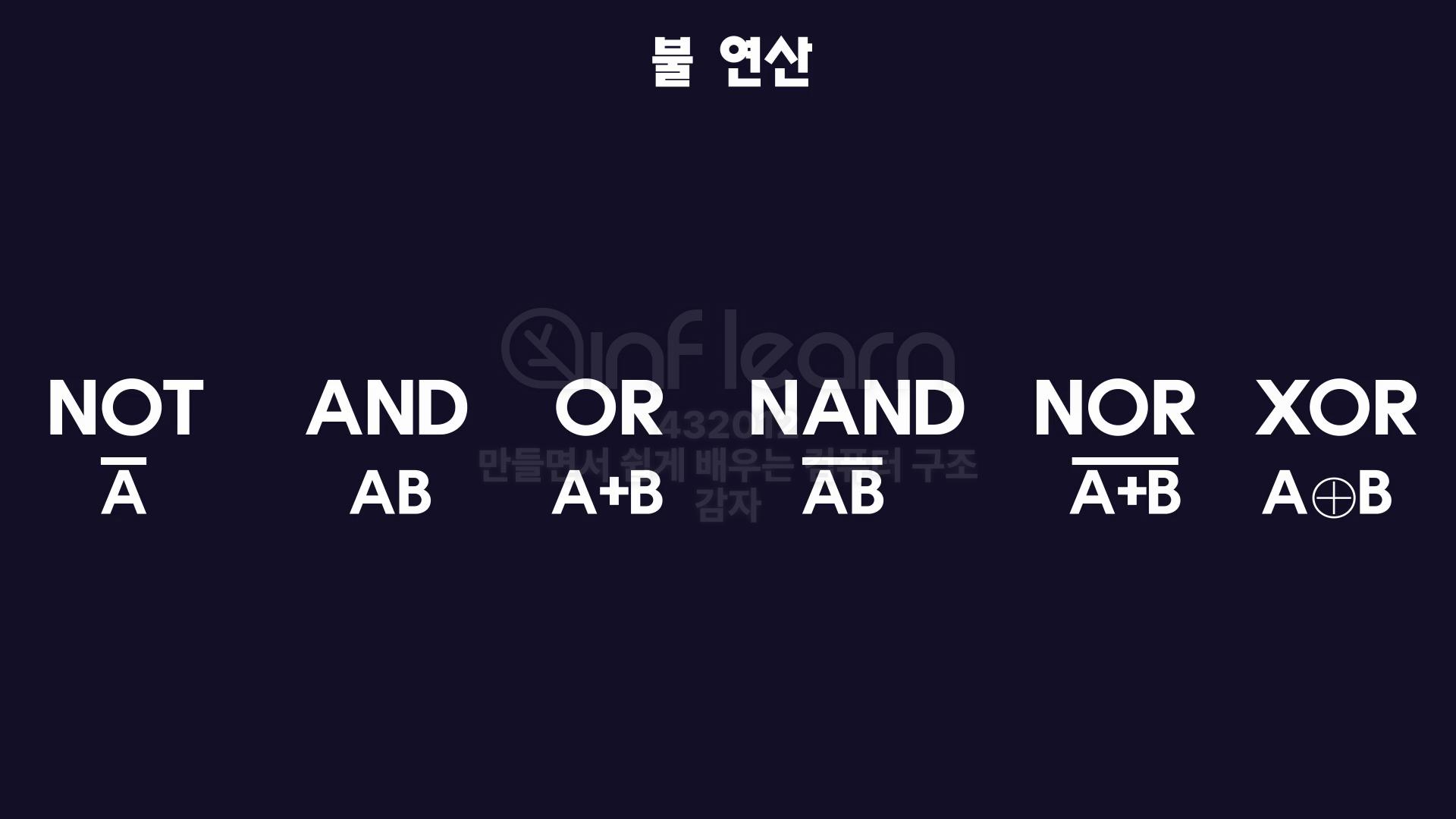
NOT연산
- 입력값을 반전함.
- 입력 A (A=1) 👉🏻 출력은 0

- 불대수에서 NOT 연산 표현시 작은따옴표(') 혹은 변수 위에 Bar(-) 를 붙인다. !
- 그리고 이걸 논리회로의 기호로 표현하면 아래와 같고, 이걸 NOT게이트 라고 부른다.
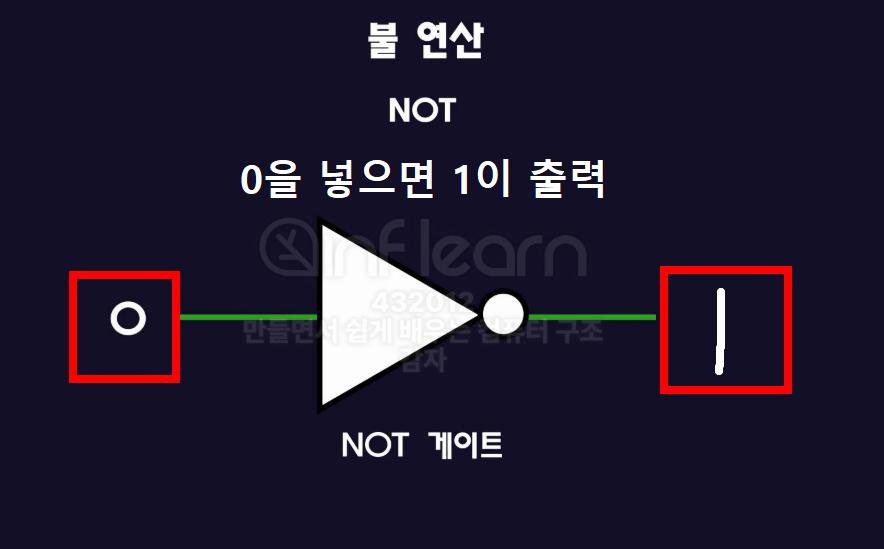
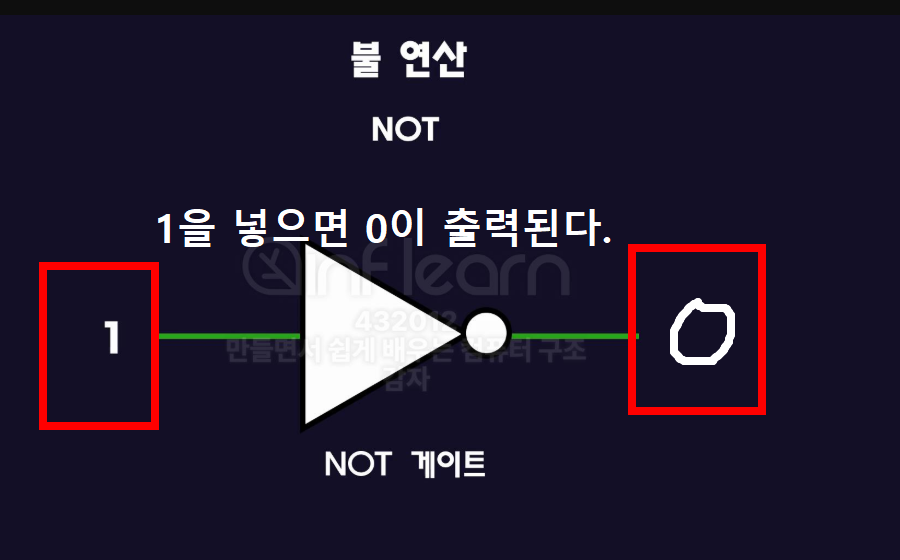
진리표
- 이처럼 입력값에 따른 출력값을 정리한 표를 " 진리표 ( Truth Table ) " 라고 함.
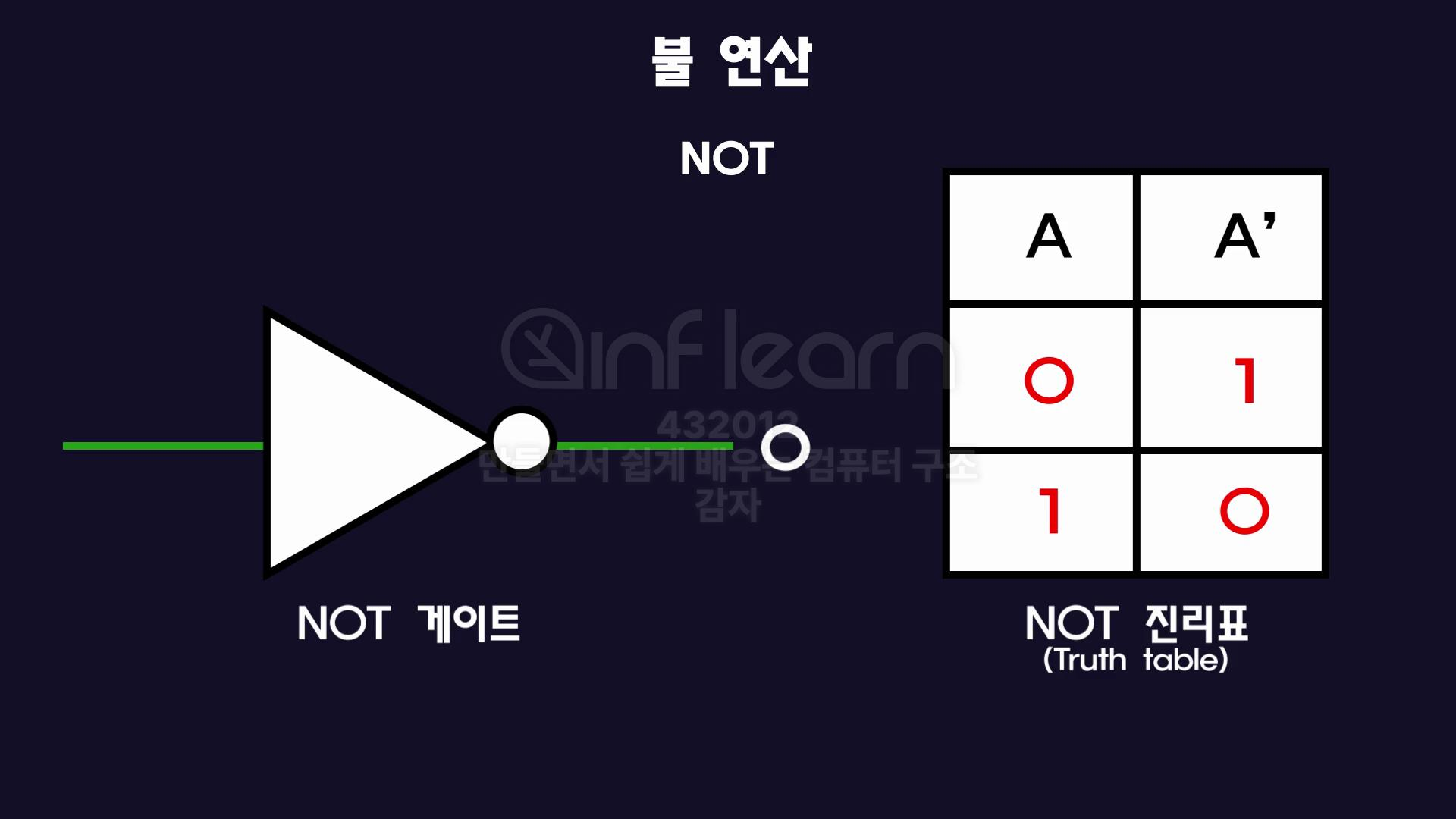
AND연산
- 2개 이상의 피연산자를 가지며, 모든 피연산가자 1일때만 결과값 1을 출력
- 그 외의 모든 경우에는 0을 출력.
진리표
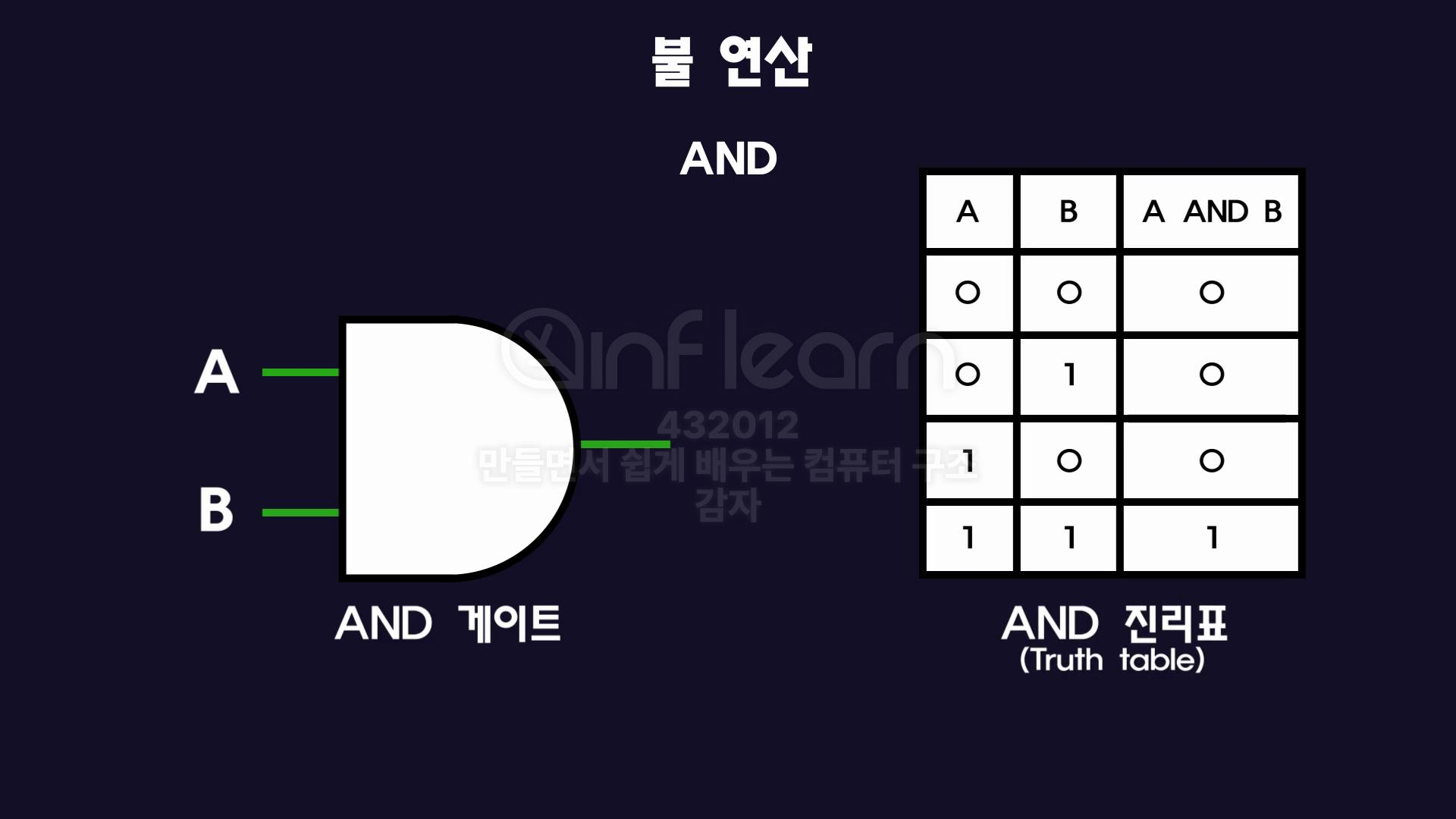
- A와 B값이 둘다 1일 때만 결과값이 1이다.
- 확인해보면 피연산자의 곱한 값이, 곧 AND연산의 결과값이다.
- 이러한 특징 때문에 AND연산 = 논리곱 = 곱셈기호로 표시
A AND B또는AB로 표기함
OR연산
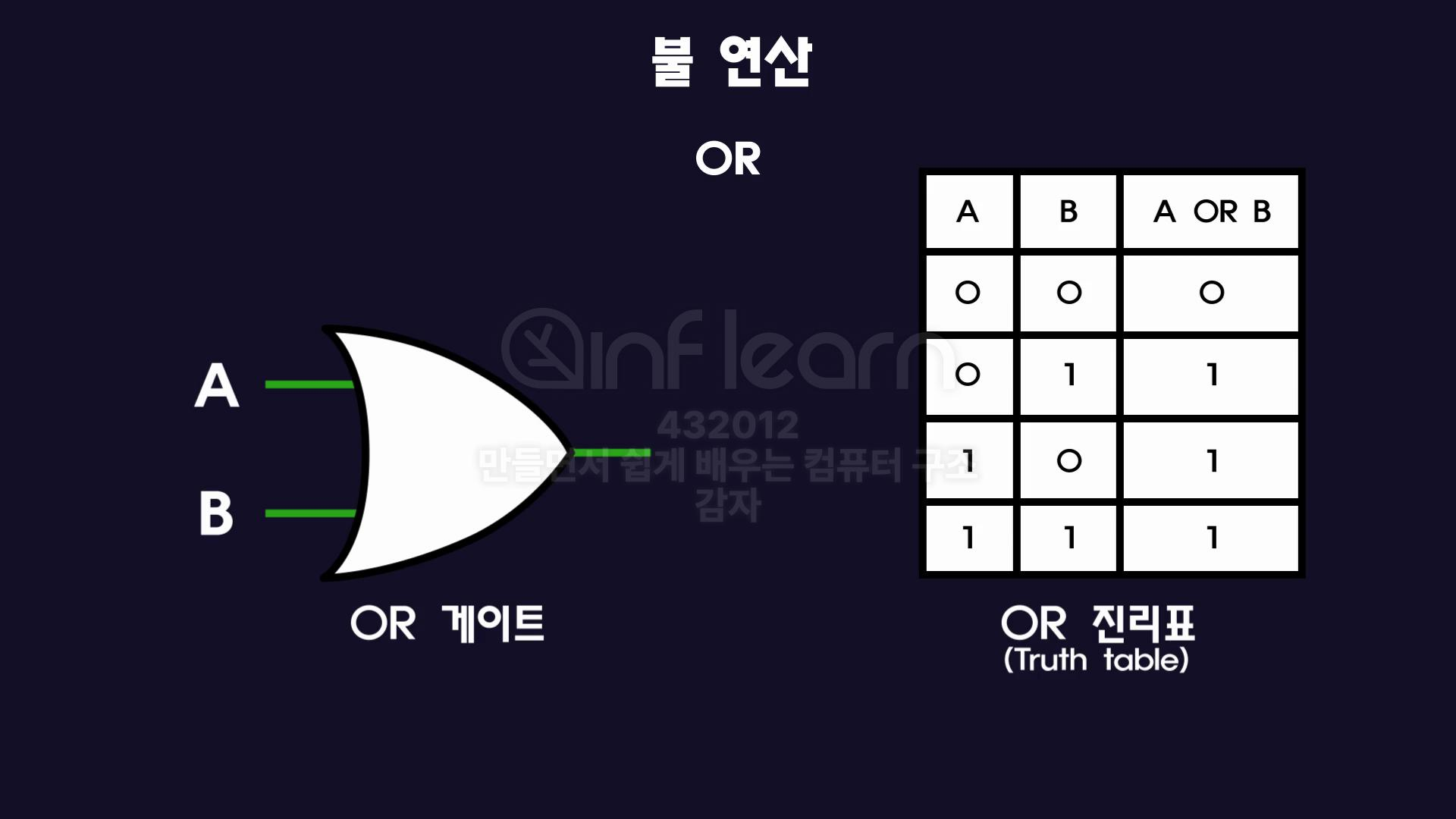
- AND와 동일하게 2개 이상의 피연산자를 가짐.
- OR게이트와 진리표를 확인해보면, 입력에 대한 두 출력값을 " 더한 것과 " 유사한 패턴을 보인다.
- 이러한특징 때문에 논리합이라고 표현
A OR B또는A+B로 표기함
어라라? 근데 진리표 마지막을 확인해보면
1+1=2인데 진리표는1로 나옴🚨진리표에서는 단순한 숫자값이 아닌 👉🏻 거짓과 참으로 나타내는
논리값이다.
NAND연산
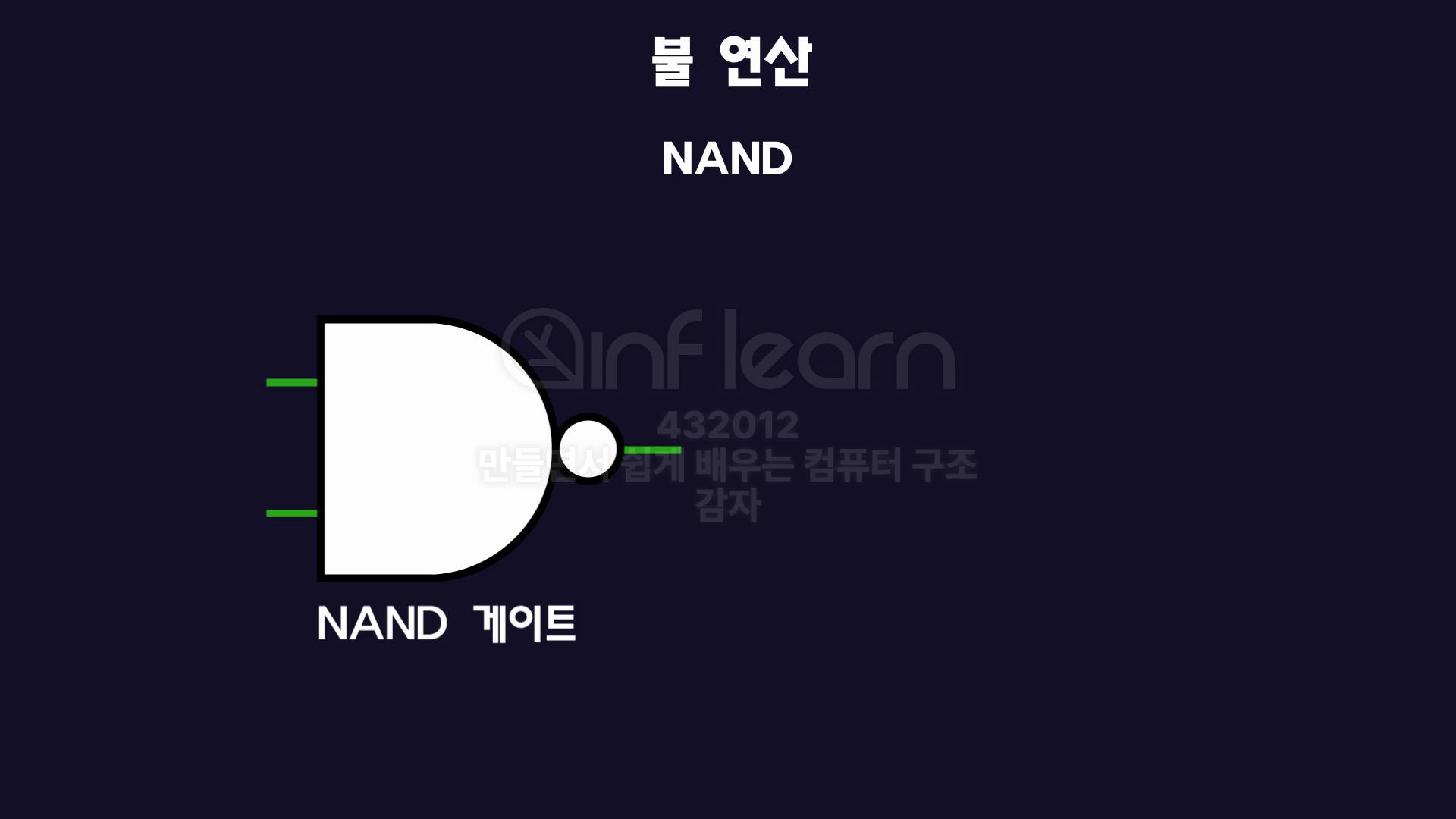
- 논리회로로 확인해보면 , AND게이트에 동그라미 하나가 더 추가된 모습
- 그래서 AND연산의 결과값 + NOT연산(동그라미) 한번 더 해야함
- 그렇다보니 AND연산의 정 반대값
- 표현식은
AB위에-를 올려야함.
NAND게이트의 중요성
- 디지털회로에선 이 NAND게이트가 가장 중요하다.
- 이 게이트로 모든 논리회로를 구현할 수 있다.
- 실습시간에 좀더 자세히 알아보겠다.
NOR연산
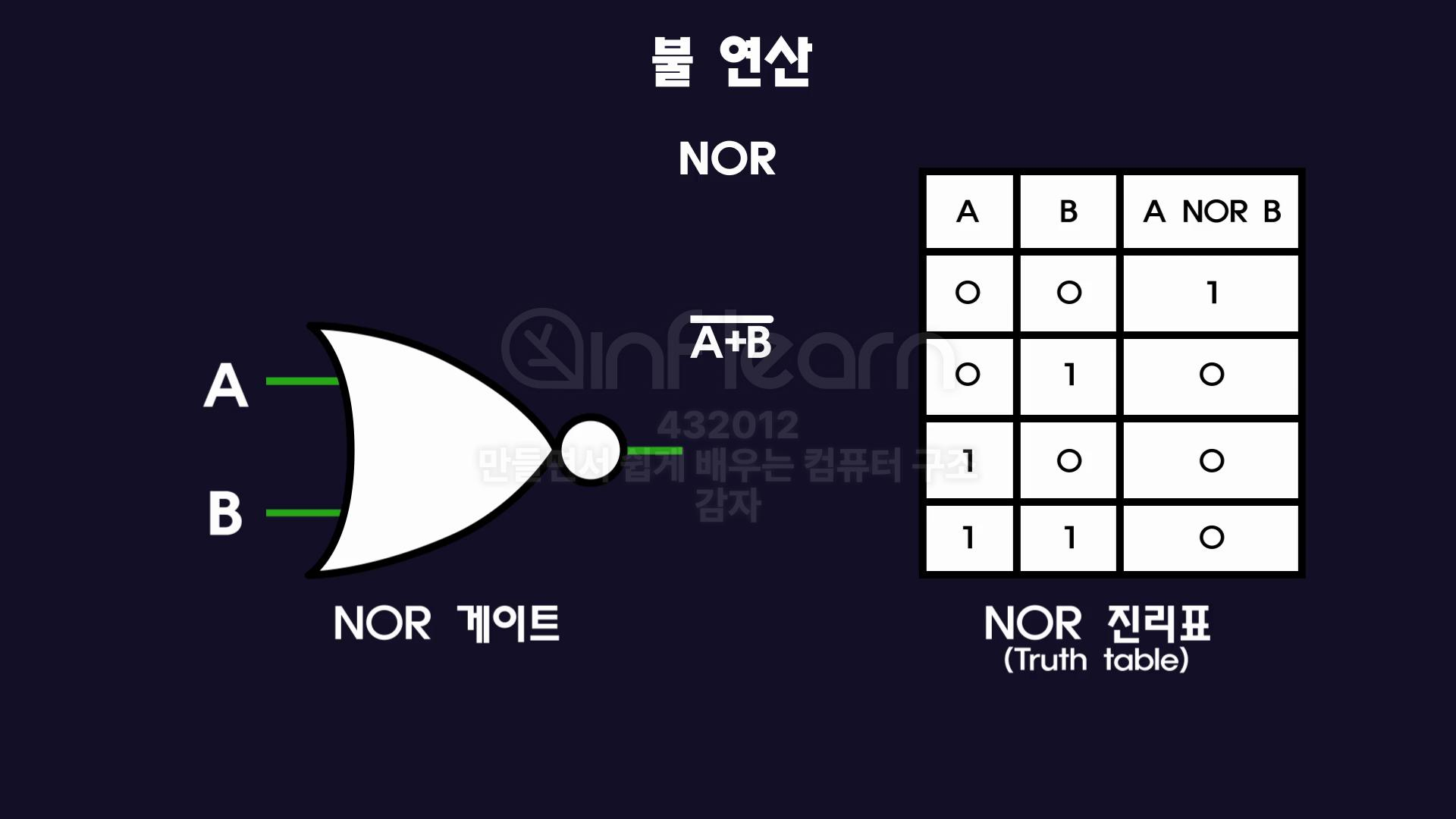
- OR게이트에 동그라미 하나 더 추가
- OR연산의 결과값 + NOT연산
- OR값의 반대
- 표현식은
A+B위에-올리기.
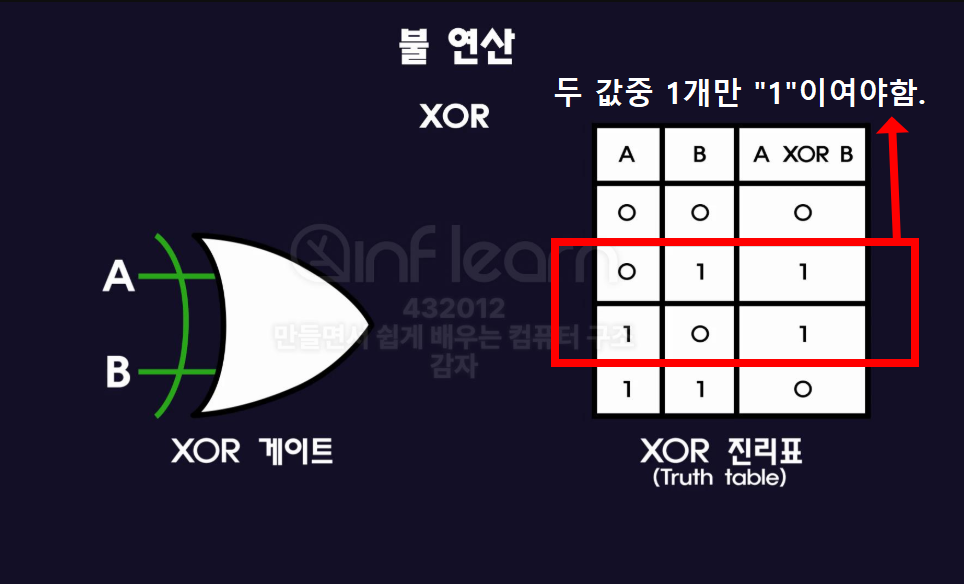
XOR연산
- OR게이트와 비슷하지만, 입력부에 세로줄이 하나 더 있음.
- 입력값중 1개만
1이여야지 , 결과값으로1반환함. - 활용 : 두 입력이 다른지 검사 할 때 사용됨 (왜냐하면, 두 입력이 다르면 결과값이
1이 나오기 때문 )
불 연산의 마무리
2️⃣불 대수의 성질과 법칙
항등원 성질
- 어떤 수 A와 연산했을 때, 결과값이 A가 되도록 해주는 값B를 항등원 이라고함.
- 예시로 덧셈에선
0이 항등원, 곱셈에선1이 항등원 이다. - 이는 불대수에서도 동일하게 적용된다.

AND(논리곱) 의 항등원은
1, OR(논리합)의 항등원은0
불대수 법칙
1. 교환법칙
- 피연산자들의 순서를 바꿔도 결과가 같다는 성질
2. 결합법칙
-
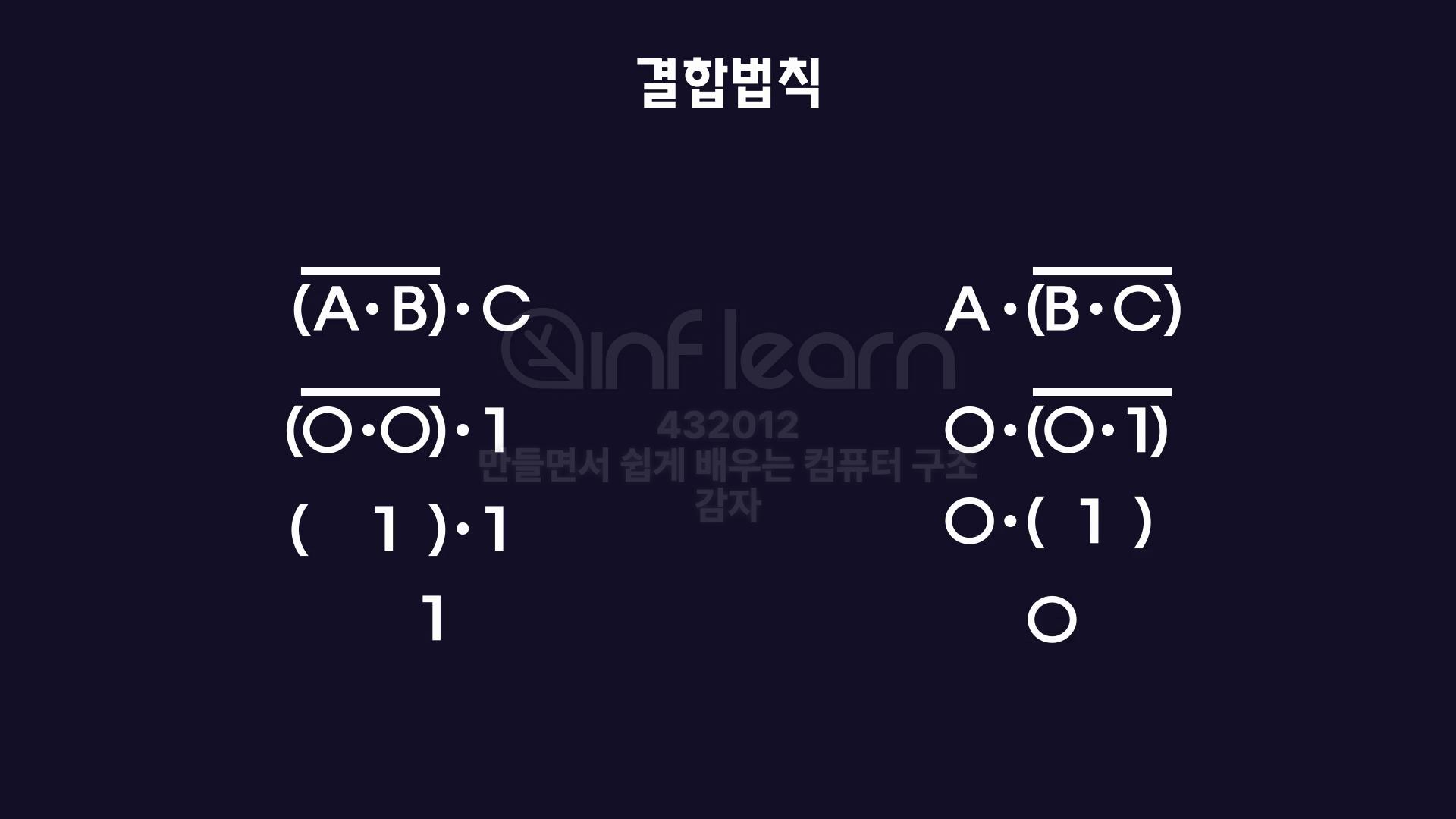
3개 이상의 항을 연산할 때, 어느 두항을 먼저 계산하더라도 , 최종결과는 같다.
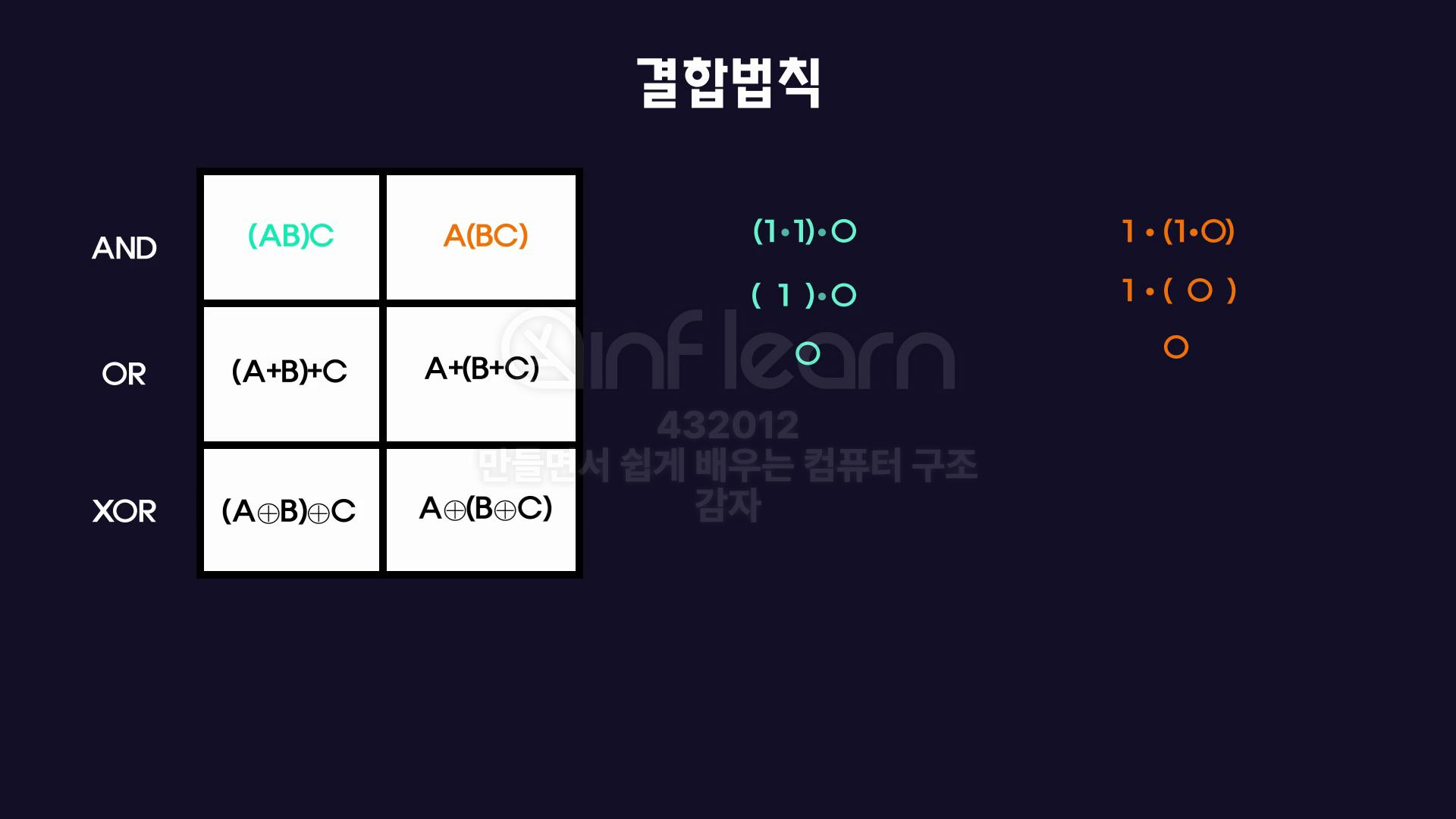
-
🌿주의사항 :
NAND,NOR,XNOR연산에는 적용되지 않는다.
3. 분배법칙
NAND,NOR,XNOR연산에는 적용되지 않음 주의
4. 동일법칙
AND,OR연산에서 같은 값을 두번 연산해도 결과가 그 값과 같다.AA = A,A+A=A
5. 이중부정법칙
- 어떤 변수를 두번 부정하면, 원래값으로 돌아온다는 성질
(A')' = A
6. 흡수법칙
- 복잡한 식이
A하나로 흡수되는 법칙으로 지금까지 배운 법칙들로 "증명"이 가능함.
A(A+B)=A
#분배법칙
(AA)+(AB)=
#동일법칙
A+(AB)=
#항등원으로 깔끔하게 정리(AND연산의 항등원이 1이므로 )
(A1)+(AB)=
#분배법칙
A(1+B)=
#A OR B는 관계없이 항상1로 고정
A(1)=
#최종값
A🚨사실 흡수법칙 증명과정이 이해가 잘 안감
7. 드모르간 법칙

- A와B의 NAND연산은
NOT AORNOT B연산과 같다 - A와B의 NOR연산은
NOT AANDNOT B연산과 같다 - 식을 정리하는데 가장 많이,자주 사용되는 법칙
✳️ 실무에서도 유용한 법칙이니 꼭 기억하자
🤔추가공부 : 드모르간 법칙 증명하기
3️⃣불 함수
- 함수 : 입력값에 따라 출력값이 달라짐.
- 불함수 : 입력+출력값이 모두
참 or 거짓인 함수.
# 두 변수를 AND연산하는 함수
f(A,B) = AB = A AND B
f(1,1) = 1*1 = 1 = `참`- 불함수 방정식에서 진리표로 / 진리표에서 논리회로 / 진리표에서 방정식으로 변환 가능.
방정식 👉🏻 진리표
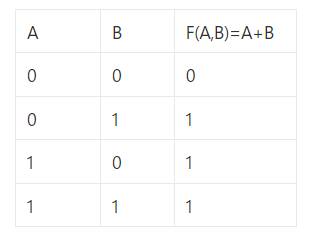
f(A,B) = A OR(+) B
- 변수가 2개이므로 4가지 경우의 수 --> 진리표 행을
4개로 만들기
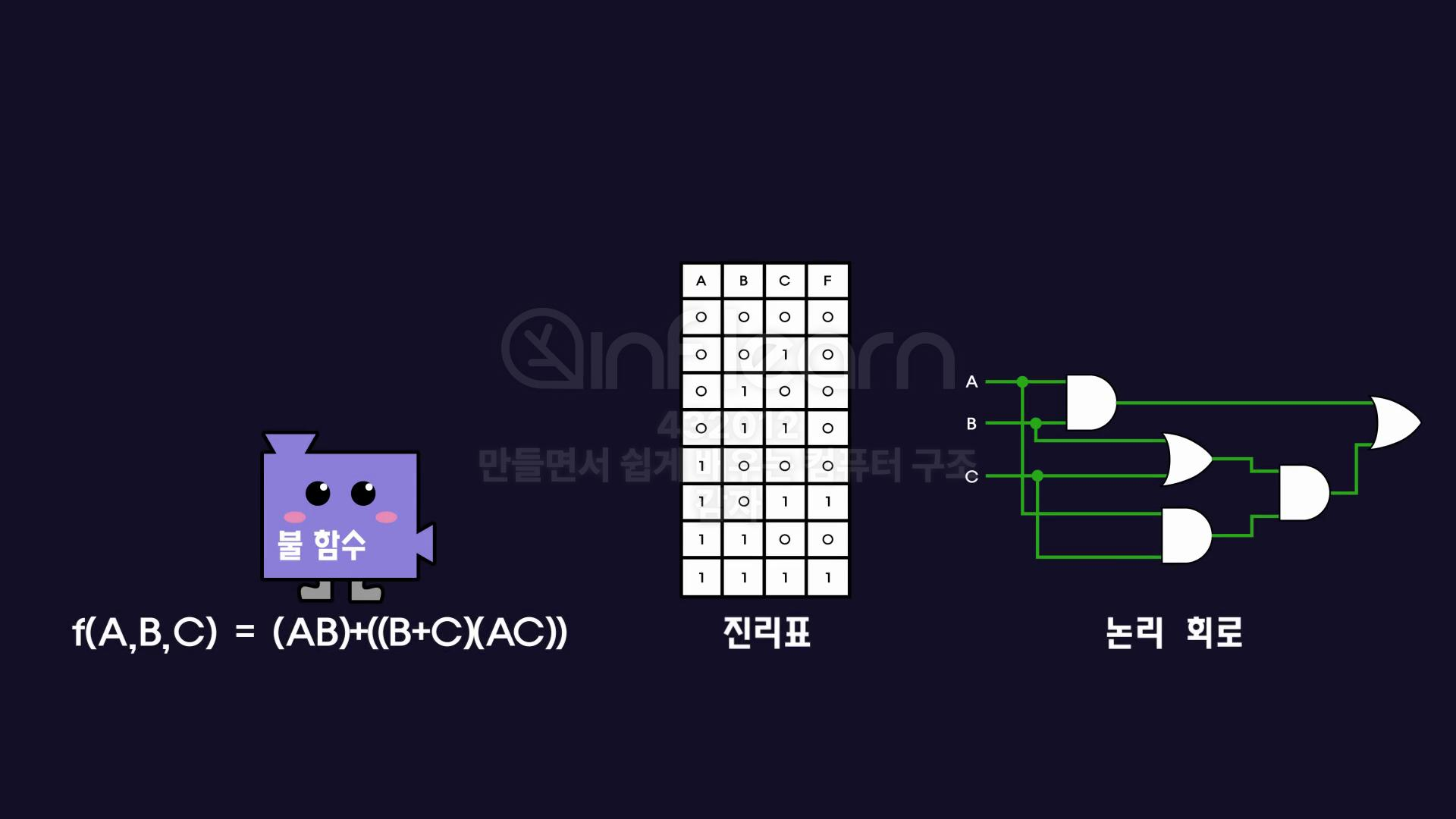
방정식 👉🏻 논리회로
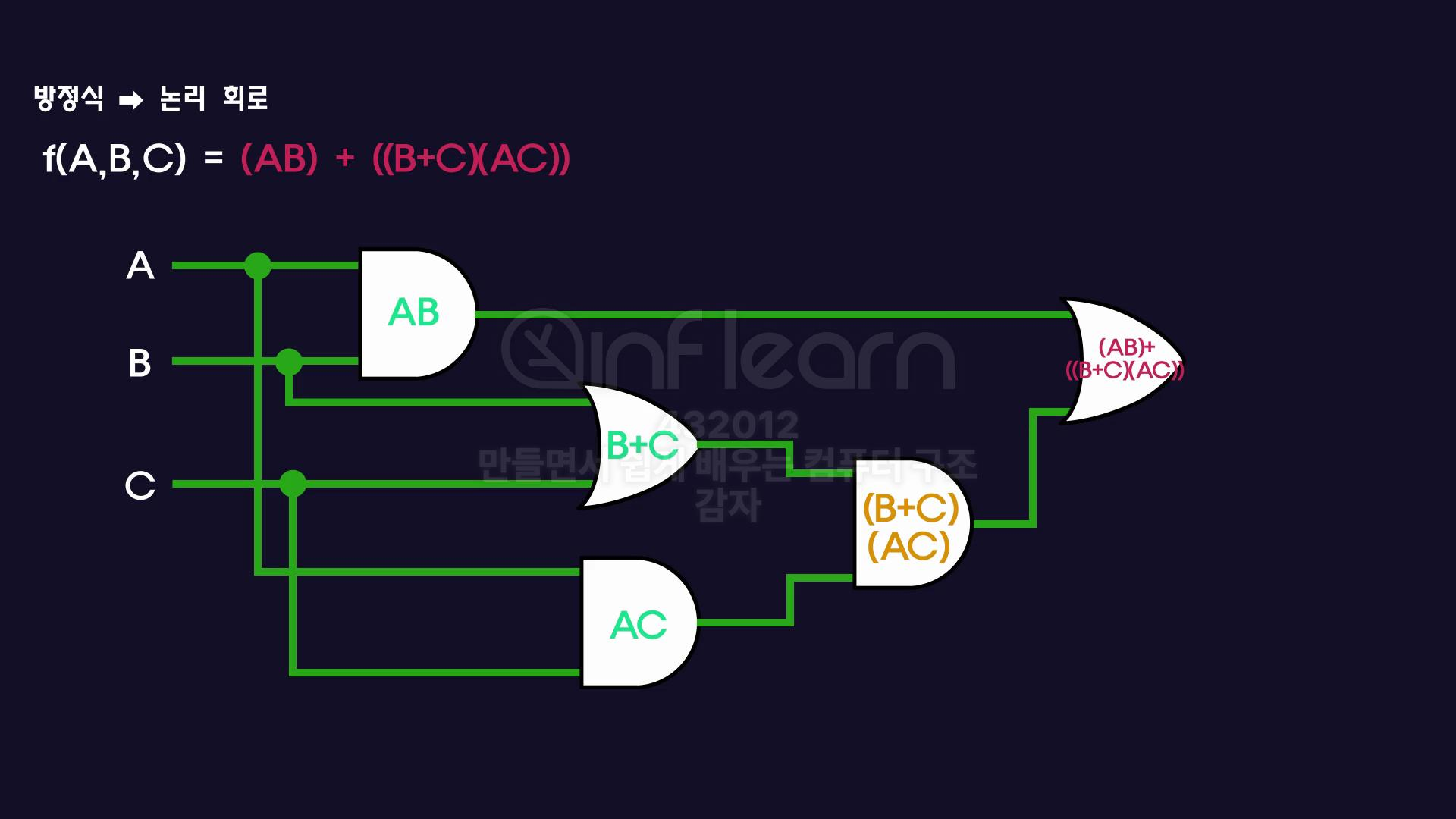
f(A,B,C) = (AB) + ((B+C)(AC))
- 단순히 연산 우선순위에 따라 , 각각의 논리 게이트를 연결하기만 하면 된다.
4️⃣진리표 변환 방법
- 진리표만 확인해보면 입력값A,B,C가 어떤 불연산들이 조합되었는지 보기가 어렵다.
- 그래서 가장 먼저 해야할 것 . 결과값이
0인 값들은 모두 제외하기
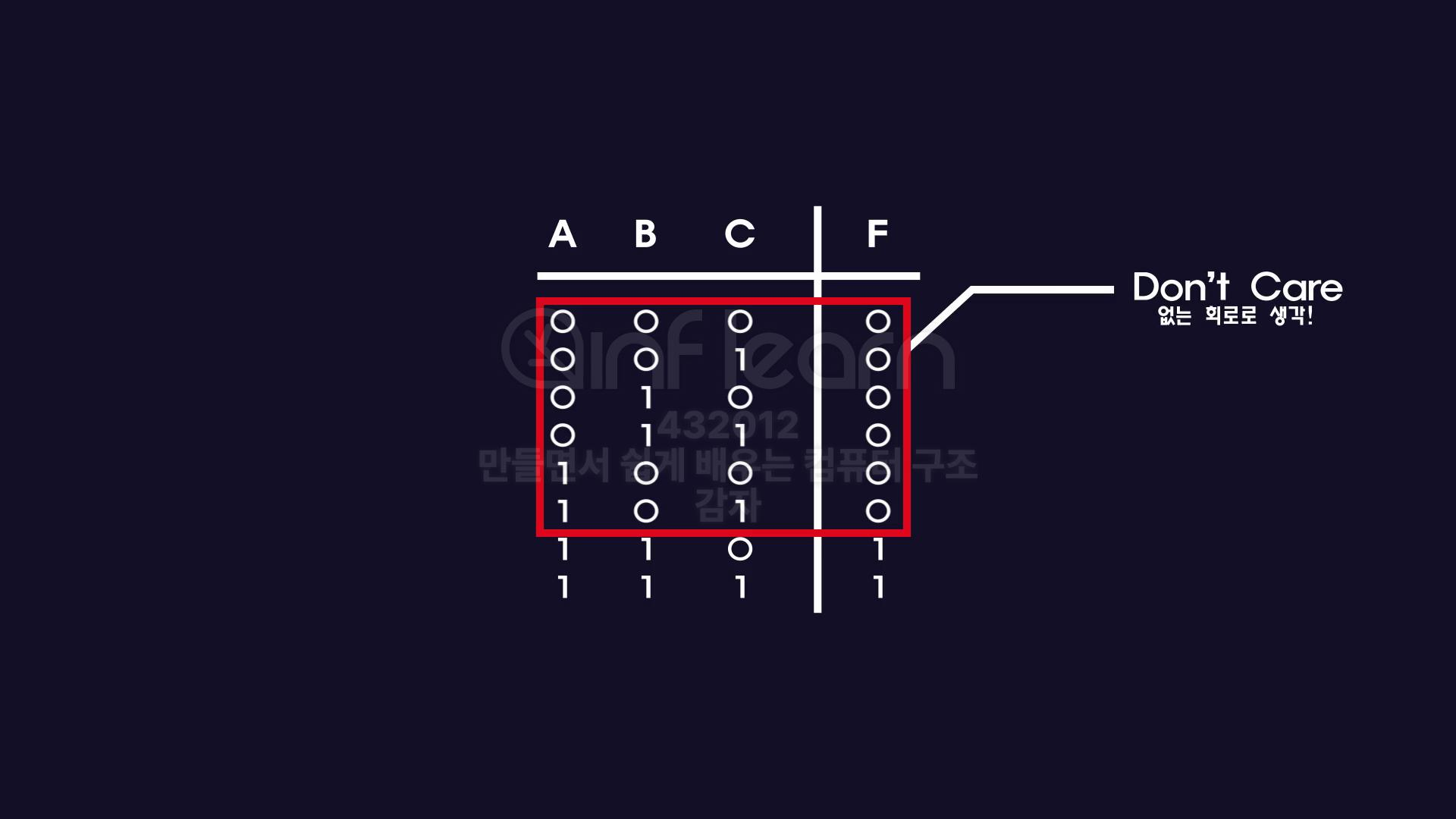
don't care행을 지우기- 남겨진 두 행으로 "방정식" 이나 "논리회로"로 변화시키기
진리표 👉🏻 방정식

- 첫번째 행 내 모든 입력을
AND로 시작해보기
f(A,B,C) = ABC
f(1,1,0 ) = 1 (거짓)- 안맞는 부분 NOT으로 바꾸기
f(A,B,C) = ABC'
= 1*1*0
= 1*1*1
= 1-
그래서 첫번째 행의 방정식은
A AND B AND C NOT -
두번째 행 내 모든 입력
AND시작해보기
f(A,B,C) = ABC
f(1,1,1) = 1*1*1 = 1
= ABC-
AND값이 참이라서 두번째 행의 방정식은A AND B AND C -
모든 행을 방정식으로 만들었으면, 각 행을
OR연산으로 묶어주기 -
(ABC')+(ABC)
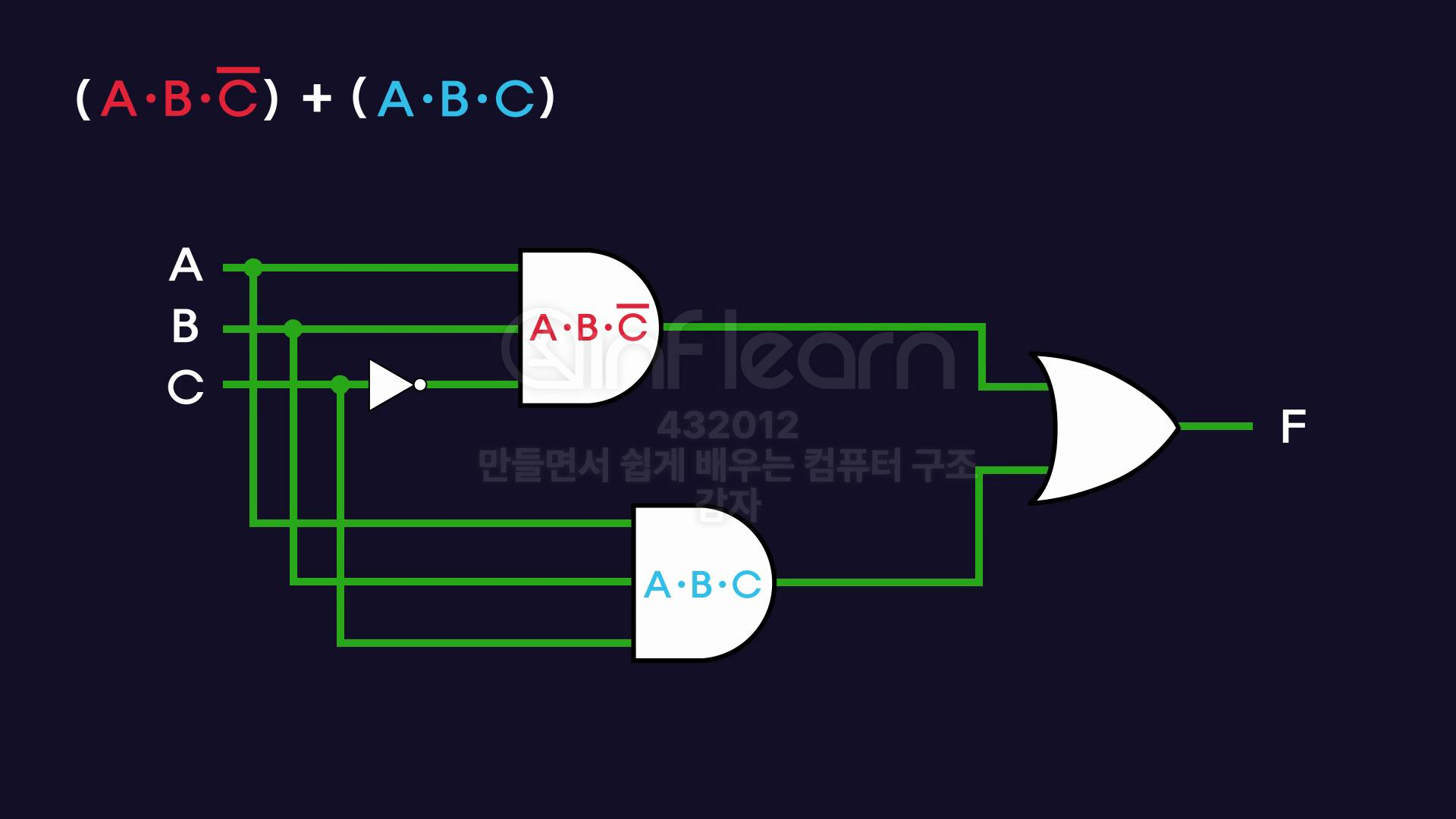
진리표 👉🏻 논리회로
방정식 값 = (ABC')+(ABC)
- 입력
A,B,C만들고 - 왼쪽 방정식에 해당하는 논리 회로 구성
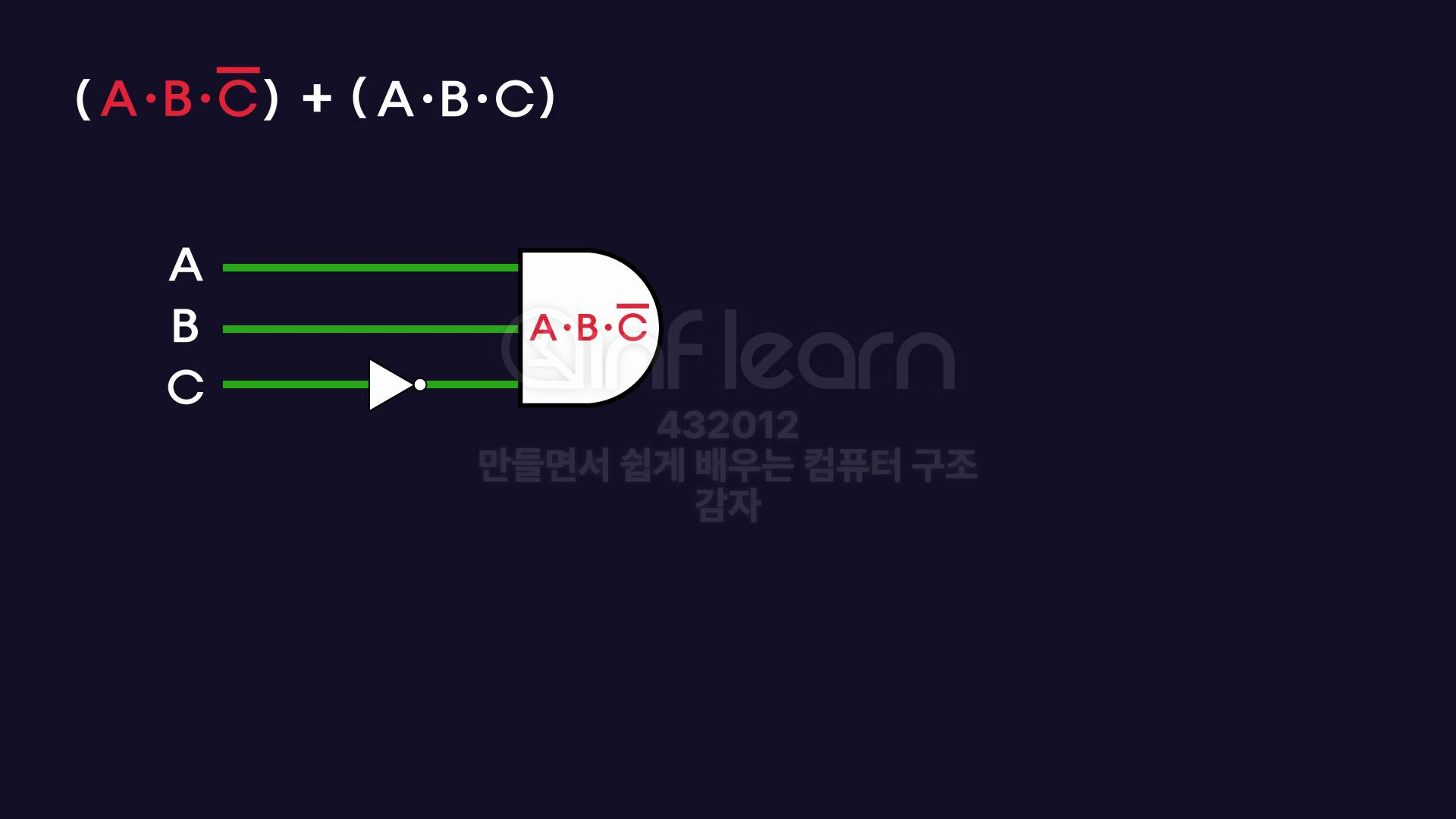
- 오른쪽 방정식에 해당하는 논리 회로 구성
- 마지막으로 두 연산 결과를
OR게이트로 연결하기 - 끝 !
(ABC')+(ABC) 방정식 리팩토링
- 불대수 법칙들을 사용하여 방정식 깔끄하게 정리하기
- 논리회로가 더 단순해지고, 필요한 부품도 줄어들어 비용 절감 및 속도 증가
(ABC')+(ABC)
# 1. 분배법칙
AB(C'+C)
# 2. C'+C = 항상 1
AB1
# 3. 분배법칙 ( 어떤수에 1을 곱해도 결과값 변하지 않으니 1 생략 )
AB
# 4. 이 값으로 논리회로 구성하면 끝
마무리
인사이트
- 이번 시간에 불대수 (0과1 또는 참,거짓으로만 표현되는 논리함수)에 대해 학습하였고, 불대수로 오늘날의 디지털회로(컴퓨터)를 표현하고 계산된다는 점을 알게되었다.
- 특히나, 불대수의 법칙으로 어려운 방정식을 쉽고 깔끔하게 리팩토링 된다는 점이 매력적이였고
- 논리 회로로(그림) 직관적으로 계산할 수 있다는 점이 흥미로웠다.
회고
- 그러나 불대수 법칙들을 증명하는 과정에서
흡수법칙과드모르간 법칙은 오늘날 가장 많이 사용되는 법칙인데, 증명 과정이 아직 익숙치 않고 확실히 이해가 어려웠다. (특히A + (A · B) = A가 왜 되는지 모르겠음). - 그래서 다음 포스팅에
흡수법칙은 진리표로,드모르간 법칙은 논리식으로 풀어보며 더 깊이 파고들어볼 계획이다.
