강의 출처
이 링크를 통해 구매하시면 제가 수익을 받을 수 있어요. 🤗

그림으로 쉽게 배우는 자료구조와 알고리즘 (기본편)
인프런 강의 - 그림으로 쉽게 배우는 자료구조와 알고리즘 (심화편)
인프런 강의 - 만들면서 쉽게 배우는 컴퓨터 구조

---

이진탐색트리 제거

제거 방법 3가지

1️⃣터미널 노드 제거

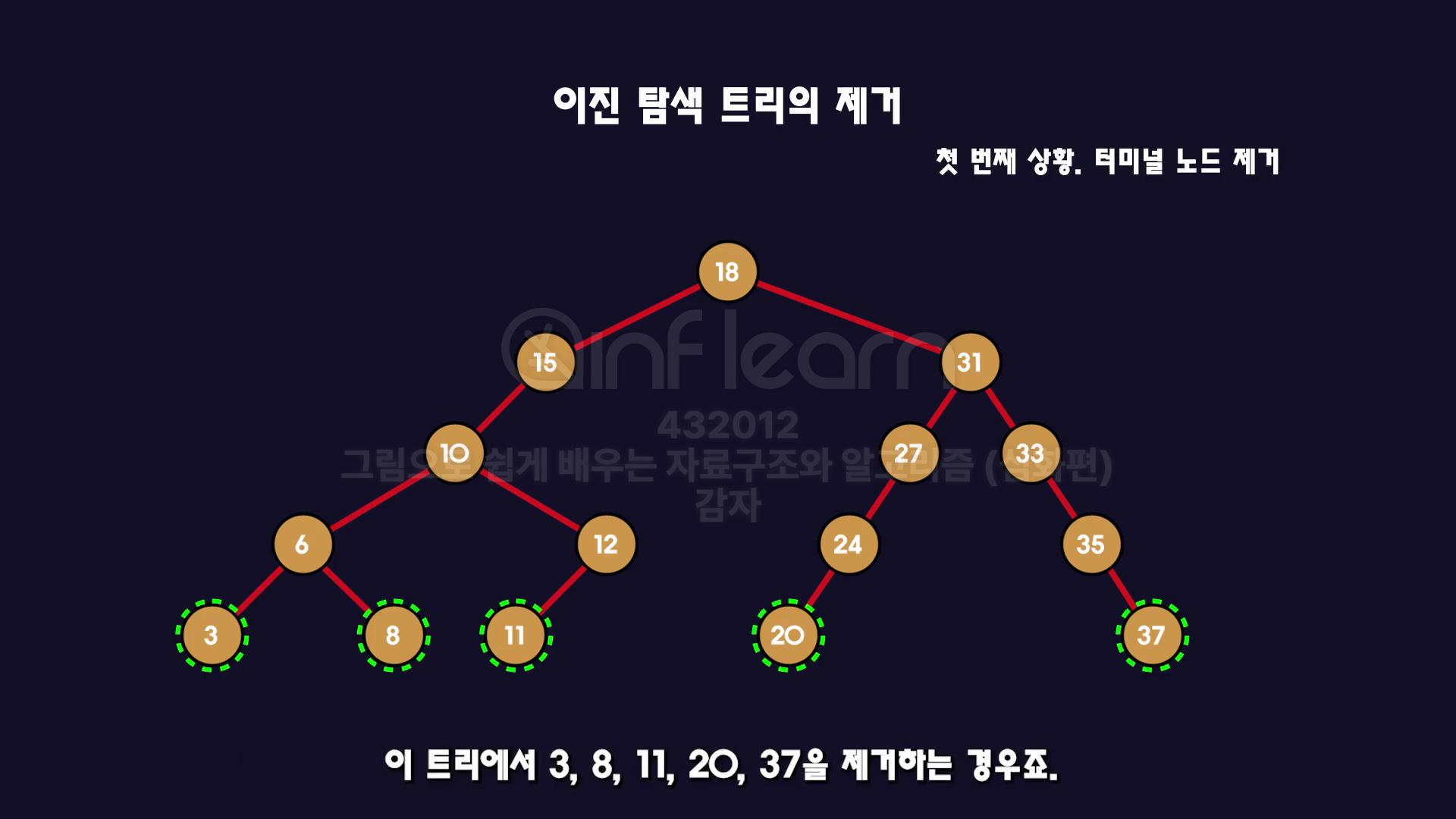
• 터미널 노드 제거는 단순히 부모노드와 연결만 끊어주면 된다.
• ( 즉 부모와의 참조를 끊어주기 )
• 그러면 간단하게 제거 된다.

2️⃣자식노드가 1개인 노드 제거

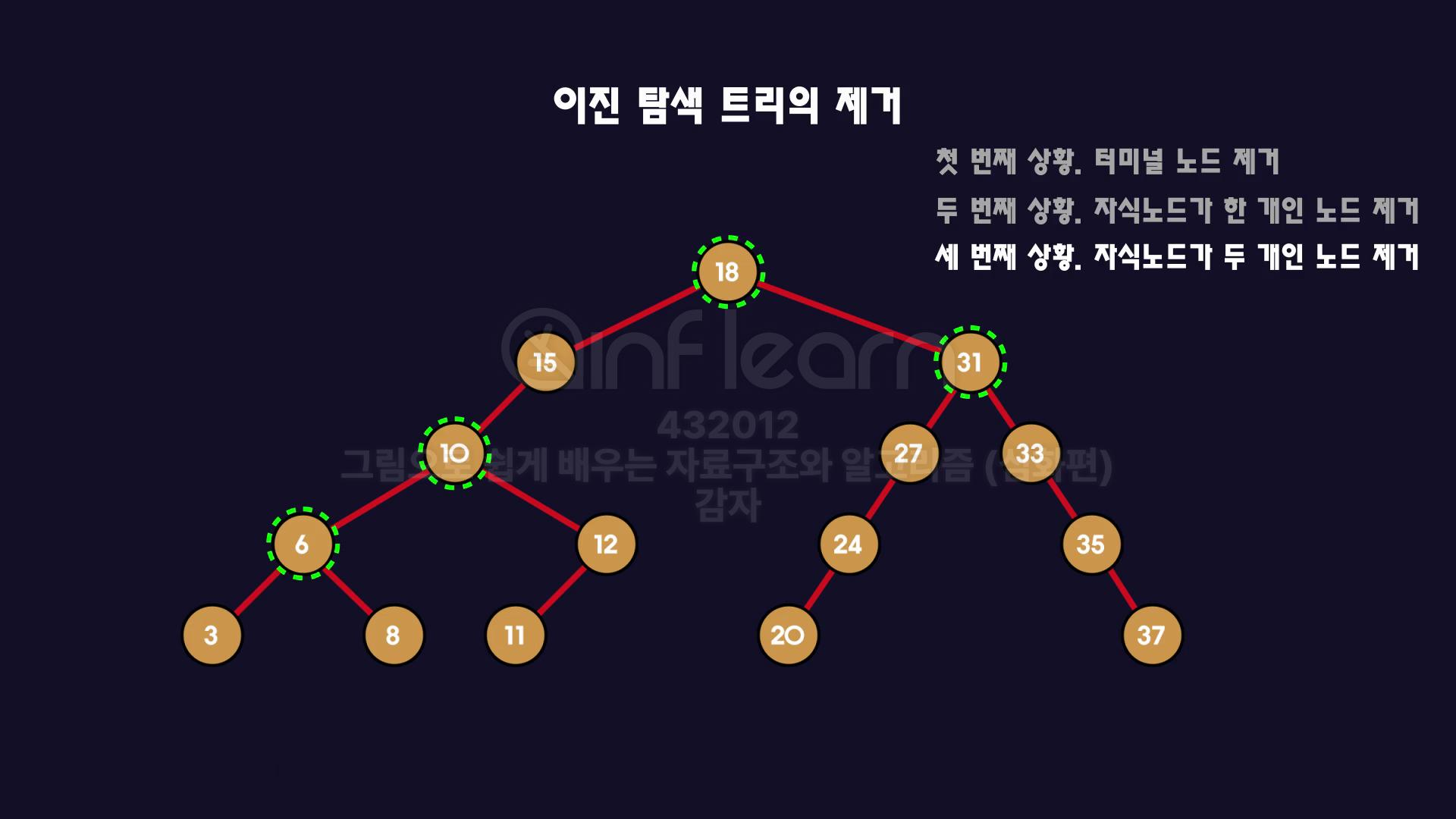
• 제거할 노드의 부모노드와의 연결을 먼저 끊어주고
• 부모노드와 , 제거할 노드의 자식노드를 연결해줘야함

3️⃣자식노드가 2개인 노드 제거

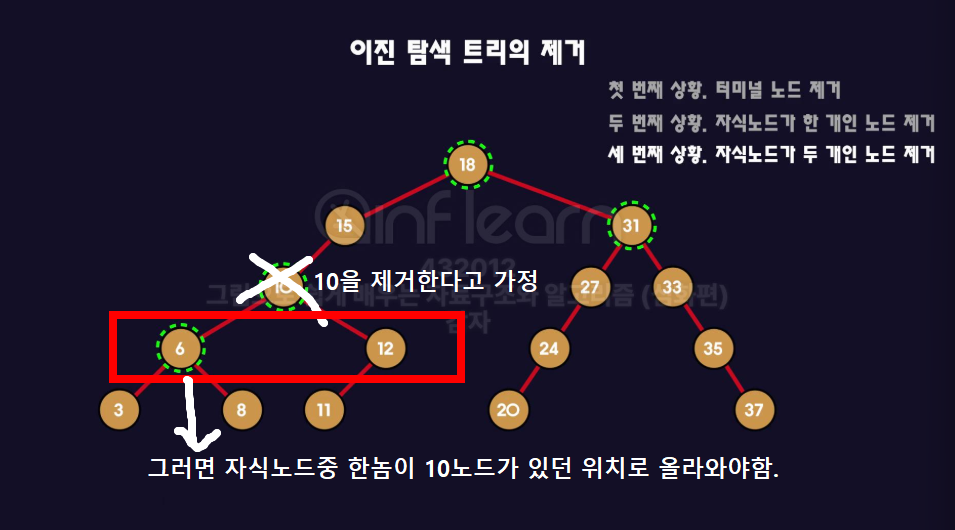
• 위와 같은 경우 이진 탐색 트리 조건을 무너뜨리지 않는 조건으로 노드가 와야함.

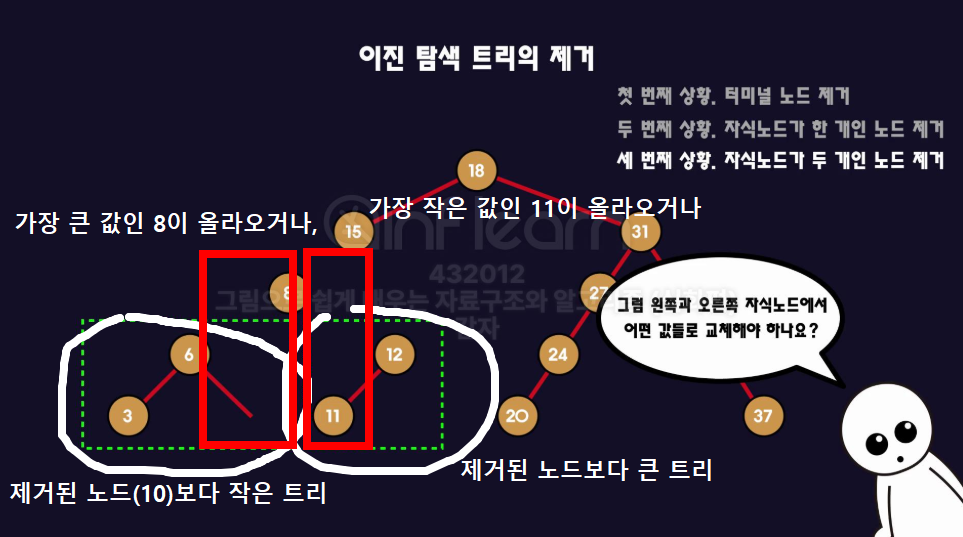
• 우리는 8을 부모노드로 올릴 예정
• 그러면 특정 트리에서 가장 큰 노드값을 찾아야함 👉🏻 이건 찾기 쉽다.
• 예시로 아래 그림을 참고해보자.
  
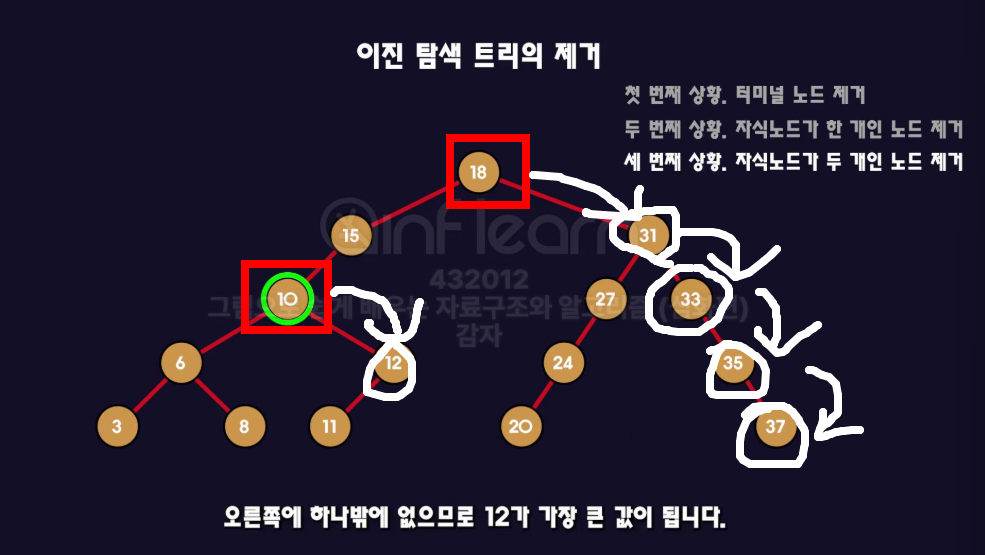
• 이렇게 특정 기준 노드를 잡고, 가장 오른쪽에 붙어있는 노드가 가장 큰 값이다.

✳️예시 - 10을 제거하는 상황 그림으로 확인하기

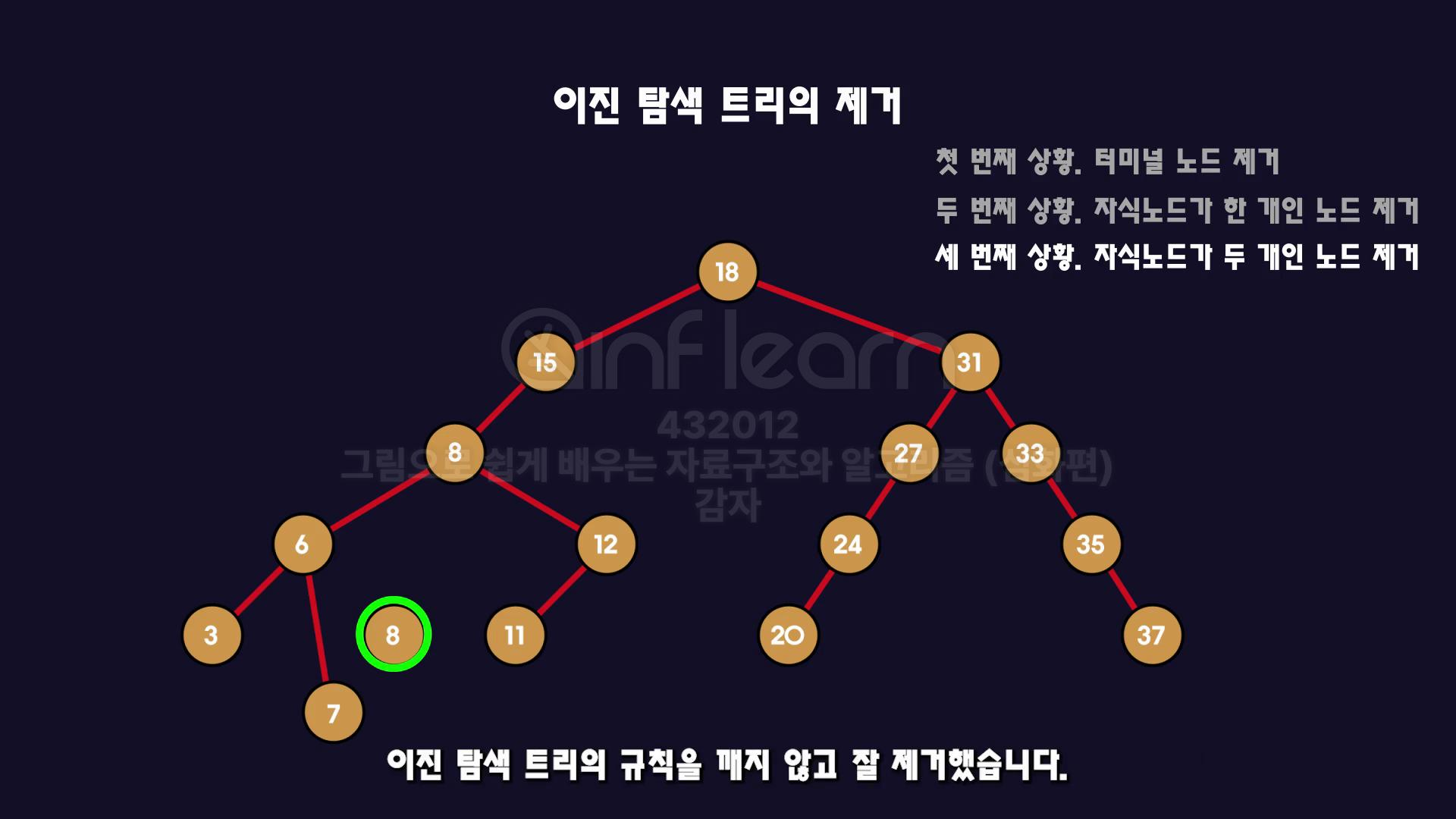
1. 제거하려는 노드의 왼쪽 자식 트리 내려가기
2. 왼쪽 자식트리에서 가장 큰 노드 찾기 ( 여기에선 8이 나왔음 )
3. 이제 8을 10노드 위치로 올려야한다.

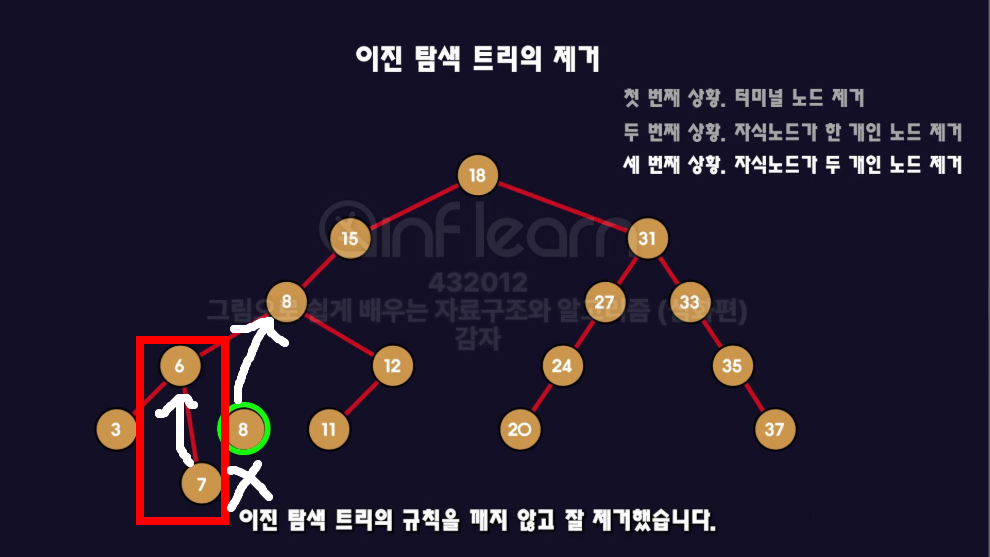
4. 그리고 위치를 옮겼으면, 8의 자식노드인 7을 연결해주기.

---

제거 구현해보기

1️⃣부가 기능 구현

1. 왼쪽 자식 노드를 제거하는 함수

 removeLeftSubTree() {
    //제거하는 노드는 변수로 반환 필요
    let deletingNode = this.getLeftSubTree();
    //그리고 왼쪽 자식노드를 null로 설정해서 끊어내기
    this.getLeftSubTree(null);
    //제거된 노드는 리턴하기
    return deletingNode;
  }

2. 오른쪽 자식 노드를 제거하는 함수

  removeRightSubTree() {
    //제거하려는 노드는 변수로 반환 필요, 선택 해야하니깐
    let deletingNode = this.getRightSubTree();
    this.getRightSubTree(null);
    return deletingNode;
  }

2️⃣변수 설정

remove(targetData) {
    let fakeParentRootNode = new BinarySearchTree(0);
  }

1. 매개변수는 제거할 데이터인 targetData로 설정
2. 루트노드의 부모 노드는 없어서, 가짜로 fakeParentRootNode 초기값은0으로 설정.

  let parentNode = fakeParentRootNode;
    let currentNode = this.root;
    let deletingNode = null;

3. 부모노드 parentNode는 현재 root노드의 가짜 부모로 설정
4. 현재노드는 root에서 시작함.
5. 삭제한 노드 deletingNode는 현재 비어있음.

3️⃣제거 할 노드 찾기

  while (currentNode != null && currentNode.getData() != targetData) {
      parentNode = currentNode;
      if (currentNode.getData() > targetData) {
        currentNode = currentNode.getLeftSubTree();
      } else {
        currentNode = currentNode.getRightSubTree();
      }
    }
    
    if (currentNode == null) {
      return;
    }

1. while문 : 현재노드가 존재하고, 제거할 데이터가 존재한다면?
2. 부모노드를 현재 노드로 초기화
3. 현재 노드를 비교해서, 크기에 따라 좌/우로 이동
4. 현재 노드 값이 타겟값보다 크다면, 왼쪽으로 내려가기
5. 현재 노드 값이 타겟값보다 작다면, 오른쪽으로 내려가기
6. 만약, 현재 노드값이 없다면? null로 비워주고 나가기.

3️⃣제거 노드 제거하는 기능 구현하기

• 위에서 이진 탐색 트리 구조에서 노드를 제거하는 접근법은 3가지 있다고 함
• 하나씩 차례대로 해보자

👩🏻‍💻 터미널 노드만 제거 ( 11 을 제거)

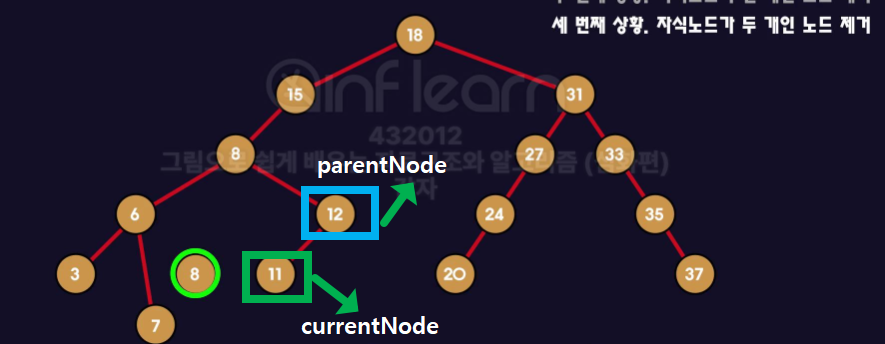
1. 제거할 노드가 헷갈리지 않도록, currentNode = deletingNode로 초기화 시키기
2. 터미널 노드만 제거 = 자식노드가 0개인 경우를 의미함
3. 그래서 자식이 없는지 확인하는 조건문 넣어야함.

if (
      deletingNode.getLeftSubTree() == null &&
      deletingNode.getRightSubTree() == null
    )

4. 확인이 끝났으면, 그 터미널 노드deletingNode가 부모노드에서 어디 위치하는지 확인
5. 왼쪽/오른쪽 노드에서 확인하고 -> remove해서 끊어주기

👩🏻‍💻 제거할 노드가 자식노드 1개 갖고 있는 경우 ( 8을 제거 )

else if (
      deletingNode.getLeftSubTree() == null ||
      deletingNode.getRightSubTree() == null
    ) {
    }

1. 제거할 노드 deletingNode의 왼쪽이나 오른쪽 중에 자식노드가 1개만 있다면 ?
2. 제거할 노드의 자식노드1개와, 제거할 노드의 부모노드를 "연결" 시켜주어야함.

let deletingNodeChild = null;
      if (deletingNode.getLeftSubTree() != null) {
        deletingNodeChild = deletingNode.getLeftSubTree();
      } else {
        deletingNodeChild = deletingNode.getRightSubTree();
      }

3. 제거할 노드의 자식노드(1개)를 담을 변수 선언 deletingNodeChild
4. 해당 자식이, 제거할 자식의 어디에 위치한지 초기화 시켜주는 작업 👉🏻 이 작업이 끝나면 deletingNodeChild에 제거하는 노드의 자식노드가 저장되어 있음.

if (parentNode.getLeftSubTree() == deletingNode) {
        parentNode.setLeftSubTree(deletingNodeChild);
      } else {
        parentNode.setRightSubTree(deletingNodeChild);
      }

5. 이제 8의 부모노드(= parentNode) 와 8의 자식노드(=deletingNodeChild)를 연결 해주면 끝이다 !
6. 제거할 노드가 부모노드의 왼쪽에 있다면? 제거될 예정이니, 자식노드를 연결 set 해줘야하고
7. 만약 제거할 노드(8)가 부모노드의 오른쪽에 있다면? 이 비어있는 자리를 자식노드가 (deletingNodeChild)로 세팅해줘야한다.

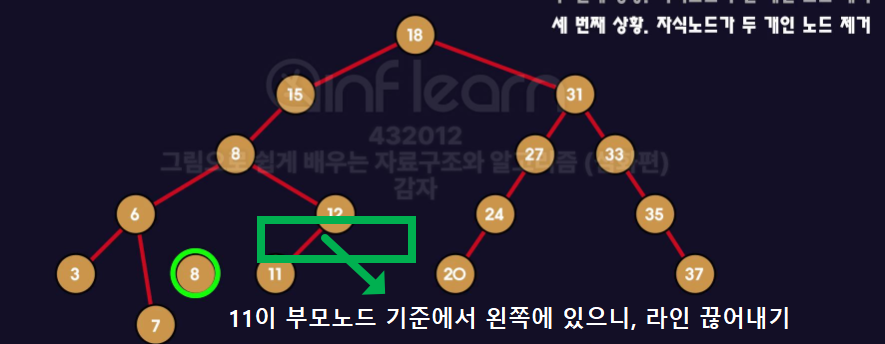
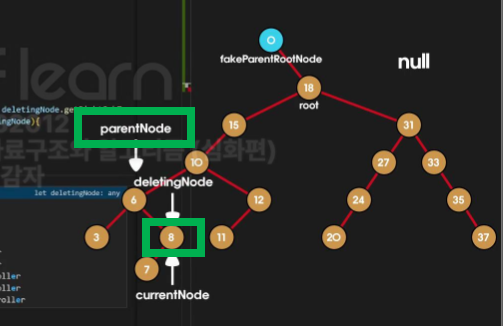
👩🏻‍💻 제거할 노드가 자식노드 2개 갖고 있는 경우 ( 10을 제거 )

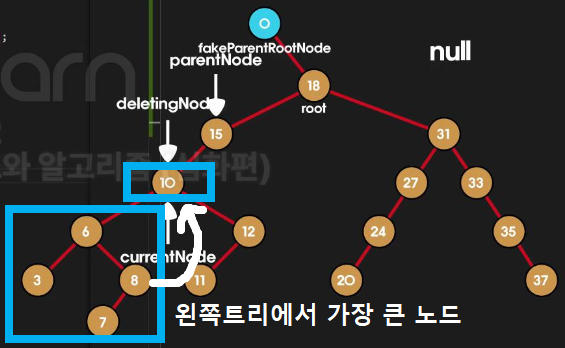
10을 제거하는 경우, 왼쪽 트리에서 가장 큰 노드로 대체해야함.

< 기본 >

• 우리가 이미지에서 확인했던 제거순서는 아래처럼 친행되었다.

1. 8이 대체되었으니, 8자리에는 8의 자식인 7이 6의 오른쪽 노드로 와줘야함.
2. 10 노드를 제거
3. 10의 자리에 8 노드 연결
4. 15의 왼쪽 자식을 8노드 연결 + 8의 왼쪽 자식으로 6 연결 + 8의 오른쪽 자식으로 12연결

< 대체 >

• 그러나 , 10노드를 제거하는 것 보다 8노드로 값을 변경해주면 번거롭게 연결하지 않아도 된다.

1. 8이 대체되었으니, 8자리에는 8의 자식인 7이 6의 오른쪽 노드로 와줘야함.
2. 10노드의 값을 8로 변경 ( 이렇게 하면, 10노드를 제거하느라 연결을 끓을 필요가 없음 )
3. 끝