[test]소수 찾기 - 파이썬

Q.

[문제 설명]
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.
소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다.
(1은 소수가 아닙니다.)
[제한 조건]
n은 2이상 1000000이하의 자연수입니다.

입출력 예
n	result
10	4
5	3
입출력 예 설명
입출력 예 #1
1부터 10 사이의 소수는 [2,3,5,7] 4개가 존재하므로 4를 반환
입출력 예 #2
1부터 5 사이의 소수는 [2,3,5] 3개가 존재하므로 3를 반환

my A.

1st Try

def solution(n):
    answer = 1
    for x in range(3, n+1):
        for j in range(2, x):
            if x % j == 0: #나누어떨어짐
                break 
        else:
            answer += 1
    return answer

방법: 어떤 수 x에 대해 그보다 작은수들을 범위로 하나하나 나눠보고 나누어떨어지면 break
-->> 시간초과 / 효율성 없음.

참고 - 에라토스테네스의 체

https://ko.wikipedia.org/wiki/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98_%EC%B2%B4

에라토스테네스의 체
python(3.6.4)으로 구현[1]

def prime_list(n):
    # 에라토스테네스의 체 초기화: n개 요소에 True 설정(소수로 간주)
    sieve = [True] * n
# n의 최대 약수가 sqrt(n) 이하이므로 i=sqrt(n)까지 검사
    m = int(n ** 0.5)
    for i in range(2, m + 1):
        if sieve[i] == True:           # i가 소수인 경우
            for j in range(i+i, n, i): # i이후 i의 배수들을 False 판정
                sieve[j] = False
 # 소수 목록 산출
    return [i for i in range(2, n) if sieve[i] == True]

결과:

prime_list(20)
[2, 3, 5, 7, 11, 13, 17, 19]
max(prime_list(1000000))
999983

2nd Try

def solution(n):
    
    sieve = [True] * (n+1)

    # n의 최대 약수가 sqrt(n) 이하이므로 i=sqrt(n)까지 검사
    m = int(n ** 0.5)
    for i in range(2, m + 1):
        if sieve[i] == True:           # i가 소수인 경우
            for j in range(i+i, n+1, i): # i이후 i의 배수 False
                sieve[j] = False

    # 소수 목록 산출
    return len([i for i in range(2, n+1) if sieve[i] == True])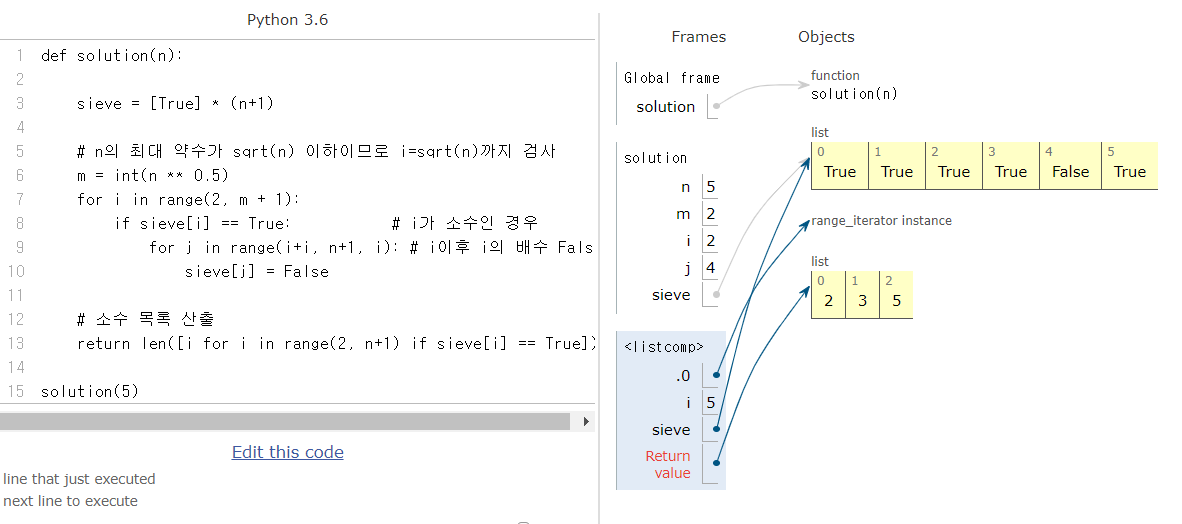

Other Sol.

def solution(n):
	num= set(range(2, n+1))
    
    for i in range(2, n+1):
    	if i in num:
        	num -= set(range(2*i, n+1, i)
            
    return len(num)

에라토스테네스의 체 간단히 구현.

• 2~n까지의 수를 함수 num에 담기
• 2~n까지의 수 i 에 대해, i 가 num 안에 있으면, i의 배수set(i의 2배수 부터 n까지수 중 i 만큼 간격있는 수들)를 num에서 빼주기
• 나머지 num의 길이 리턴