[Deep Learning] 활성화 함수 - Sigmoid 함수

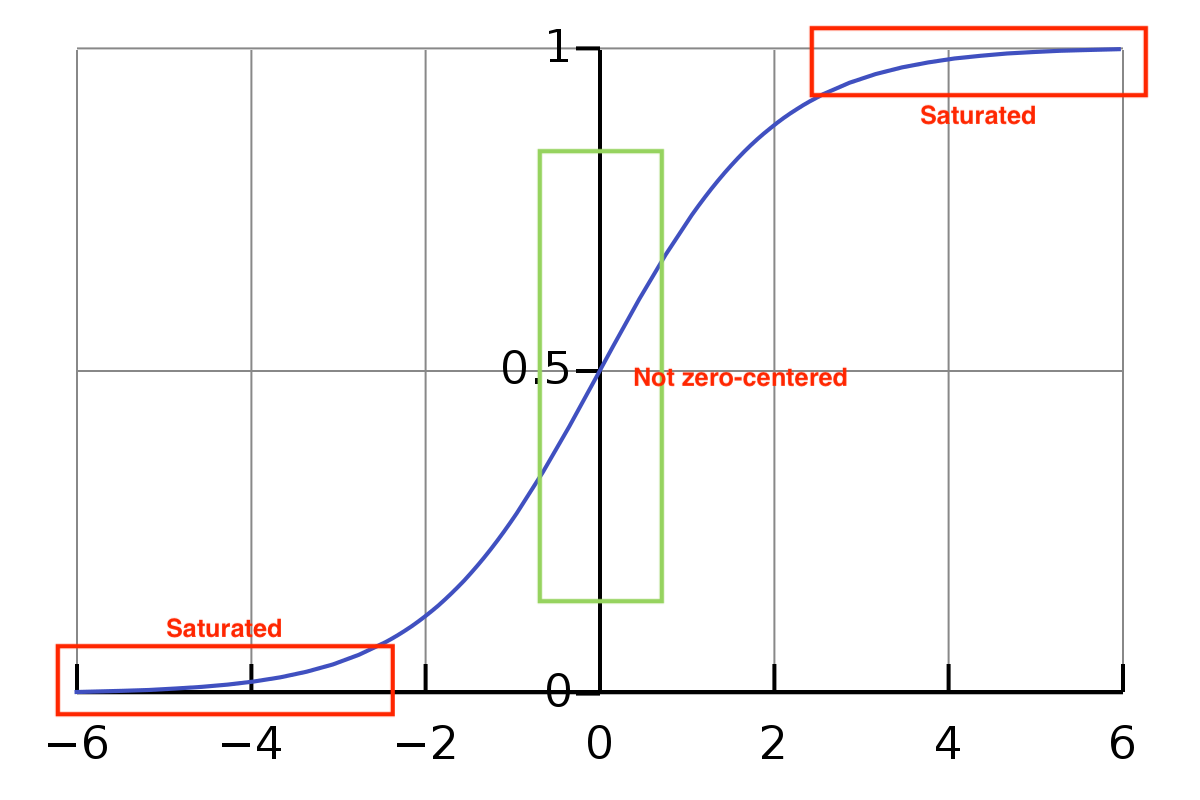
Sigmoid 함수

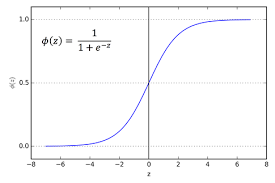
• 시그모이드 함수는 값이 들어왔을 때, 0~1 사이의 값을 반환한다.
• 값이 작아질수록 0, 커질수록 1에 수렴한다.
• Sigmoid 함수의 수식
  • $sigmoid(x) = \frac{1}{1+e^{-x}}$
• Sigmoid 함수 도함수
  - 활성화함수로 사용할 경우 경사 하강법 계산 혹은 역전파 계산 과정에서 Sigmoid 함수의 도함수가 사용된다.

  • 

  • 

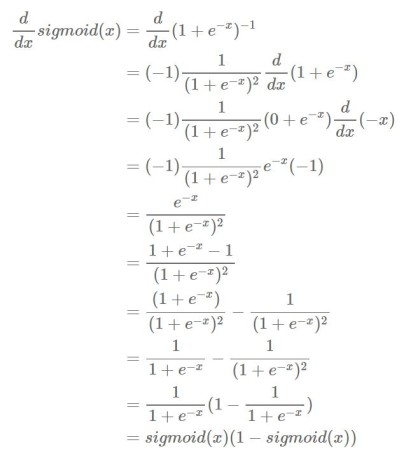
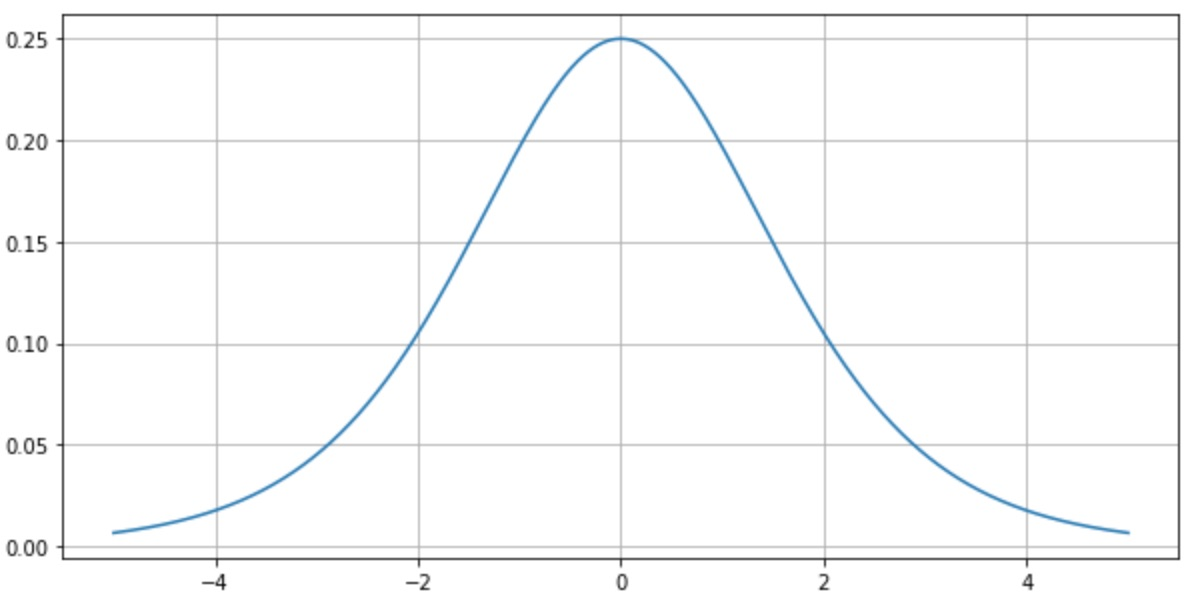
    미분계수의 최댓값은 0.25

장점

• 출력 값의 범위가 0 ~ 1 사이의 매끄러운 곡선을 가지며, 기울기가 급격하게 변해서 발생하는 Gradient Exploding(기울기 폭주)가 발생하지 않는다.
• 출력 값이 0과 1 사이로 매핑되므로 (0 혹은 1) 어느 값에 가까운지를 통해 이진 분류를 할 수 있다.
  • 데이터가 이진, 범주형이라면 시그모이드 활성화 함수를 사용하면 좋다.
• 이상치가 들어온다고 해도, 시그모이드 함수는 0과 1에 수렴하므로, 이상치 문제도 해결하는 동시에 연속된 값을 전달 할 수 있다.
  

문제

1. Gradient vanishing problem (기울기 소실 문제)

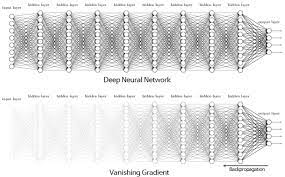
• 시그모이드 함수는 아무리 큰 값이 들어와도 0~1 사이의 값만 반환한다.
• 시그모이드 함수의 도함수는 $sigmoid(x)(1-sigmoid(x))$이므로 도함수에 들어가는 함수의 값이 0이나 1에 가까울수록 출력되는 값이 0에 가까워진다.
• 이런 이유로 수렴되는 뉴런의 기울기값(gradient)이 0이 되고, 역전파 시 0이 곱해져서 기울기가 소실되는 현상이 발생된다.
• 즉, 역전파가 진행될수록 아래 층(Layer)에 아무런 신호가 전달되지 않아 학습이 불가능해진다.

2. not zero-centered problem

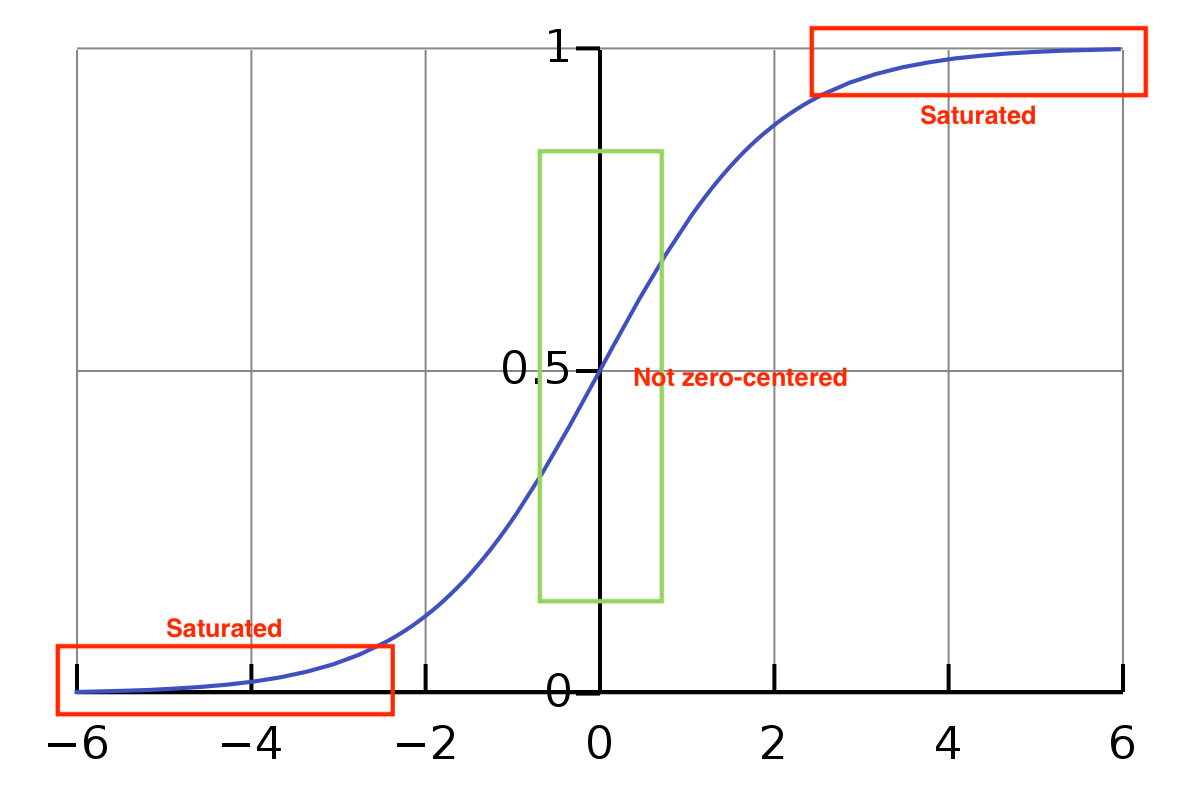
• Input 값이 항상 positive라면 W에 대한 gradient가 항상 positive(+) 또는 negative(-)가 됩니다.

• $dL/dw_1, dL/dw_2 ... dL/dw_n$ 모두 동일한 부호값이 나온다.

• 따라서 zig-zag 식의 Parameter update가 발생한다.
  
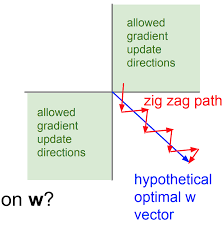
  *파란색 직선이 최적의 해

• 위의 그림과 같이 파란색 직선으로 해를 탐색하는 것이 아닌 zig-zag로 weight를 업데이트 하기 때문에 여러 번 해를 탐색해한다.

• 즉, 비효율적인 weight update가 발생하고 수렴 속도가 느려지는 문제점이 발생한다.

3. exp 연산 - 느린 연산

exp 연산으로 인해 자원과 시간이 많이 소모된다.

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()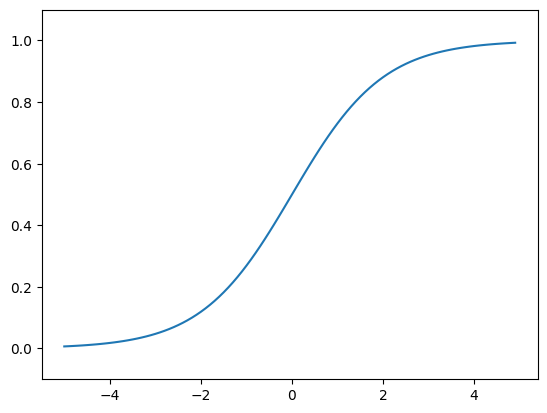

Gradient vanishing 과 not zero-centered 의 관계

• sigmoid 도함수 : $\sigma(1-\sigma)$
• 도함수에 들어가는 함수의 값이 0이나 1에 가까울수록 출력되는 값이 0에 가까워진다.
  • sigmoid 함수는 실수 값을 입력받아 0~1 사이의 값으로 매핑한다.
• 이런 이유로 수렴되는 뉴런의 기울기값(gradient)이 0이 되고, 역전파 시 0이 곱해져서 기울기가 소실되는 현상이 발생된다.

Reference

• Steve-Lee's Deep Insight님의 블로그 - [모두를 위한 cs231n] Lecture 6. Activation Functions에 대해 알아보자
  
• Why are non zero-centered activation functions a problem in backpropagation?