힙(Heap)이란?

• 최댓값, 최솟값을 빠르게 찾기 위해 고안된 자료형으로 우선순위 큐를 위해 만들어졌다.

• 완전 이진 트리의 일종으로, 각 노드의 키값이 그 자식의 키 값보다 작지않거나(최대 힙), 크지 않은(최소 힙) 완전 이진 트리이다.

완전이진트리는 중복을 허용하지 않지만 힙은 허용한다.

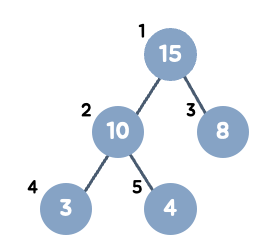
특징

힙에서의 부모 자식 관계

• 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2+1

• 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2

• 부모의 인덱스 = (자식의 인덱스) / 2

사용이유

최솟값이나 최댓값을 찾기 위해 배열을 사용하면 Ο(n)만큼 시간이 걸린다.
하지만 힙을 사용하면 O(logn)만큼 소요되므로, 배열을 사용할 때보다 빠르게 최솟값과 최댓값을 구할 수 있다.

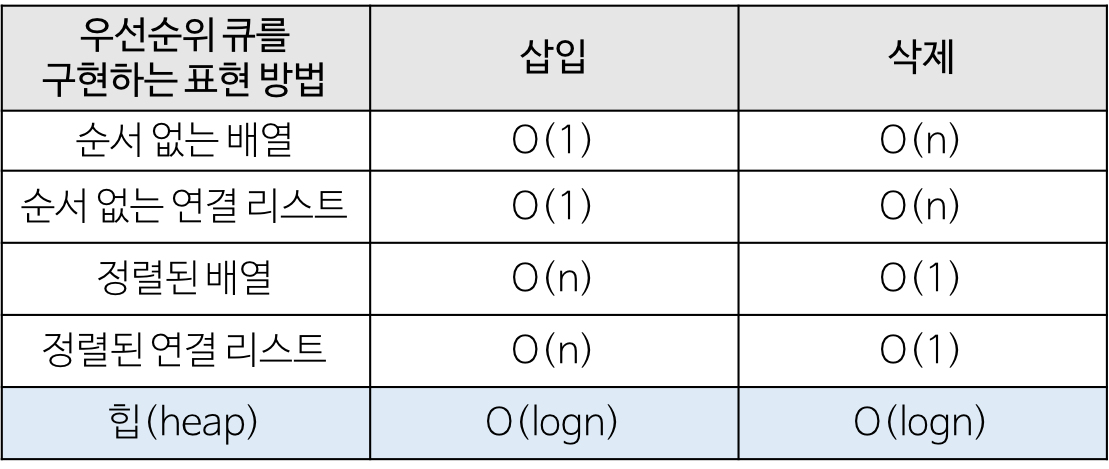
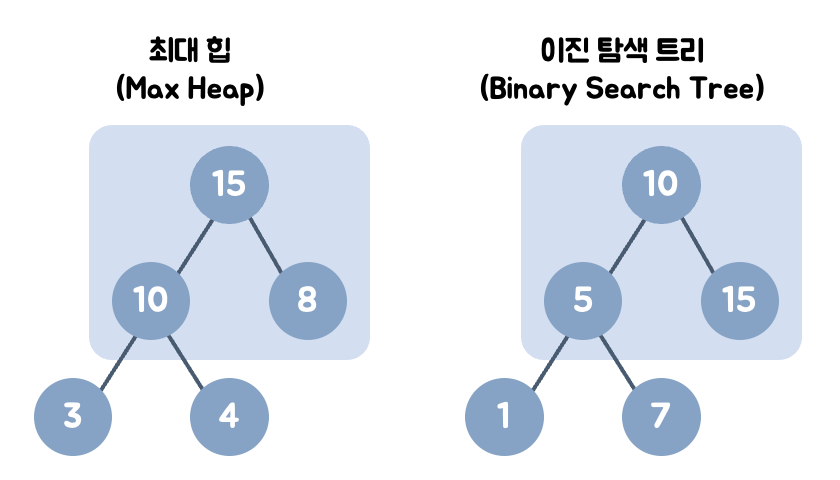
최대 힙 & 최소 힙

힙은 기본적으로 노드가 왼쪽부터 채워지는 완전 이진 트리 형태를 가진다.

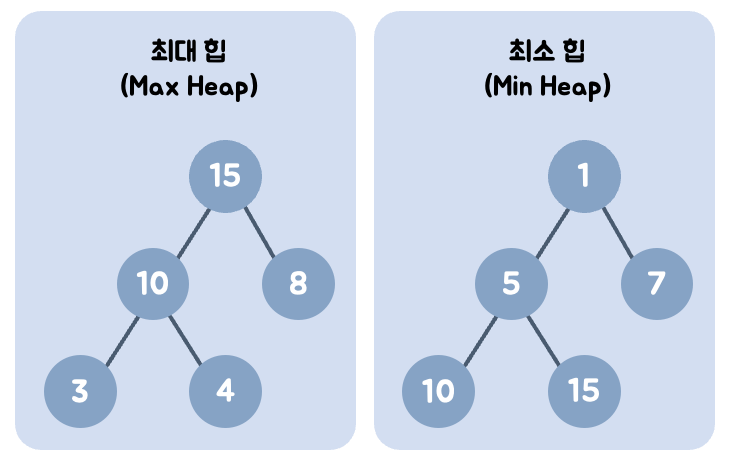
완전 이진 트리(Complete Binary Tree)란?

이진 트리에 노드를 삽입할 때 왼쪽부터 차례대로 삽입하는 트리이다.
위 그림과 같이 나타내며, 왼쪽이 비어있고 오른쪽이 채워져 있는 형태는 완전 이진 트리라고 할 수 없다.

이진 탐색 트리(Binary Search Tree)란?

이진 탐색과 연결리스트(linked-list)를 결합한 자료구조의 일종이다.
이진 탐색의 효율적인 탐색 능력을 유지하면서 빈번한 자료의 입력과 삭제를 가능하도록 한다.
각 노드에서 왼쪽의 자식 노드는 해당 노드보다 작은 값으로, 오른쪽의 자식 노드는 해당 노드보다 큰 값으로 이루어져 있다.

• 공통점
  모두 완전 이진 트리이다.
  
  
• 차이점
  최대힙의 경우에는 각 노드의 값이 자식 노드보다 크거나 같다.
  이진 탐색 트리는 각 노드의 왼쪽 자식은 더 작은 값으로, 오른쪽 자식은 더 큰 값으로 이루어져있다.
  
  왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드
  힙은 왼쪽 노드의 값이 크든 오른쪽 노드의 값이 크든 상관 없다.
  힙은 최대/최소 검색을, 이진 탐색 트리는 탐색을 위한 구조이다.

힙의 동작

데이터 삽입

힙은 완전 이진 트리이기 때문에, 삽입할 노드는 기본적으로 왼쪽 최하단부 노드부터 채워진다.

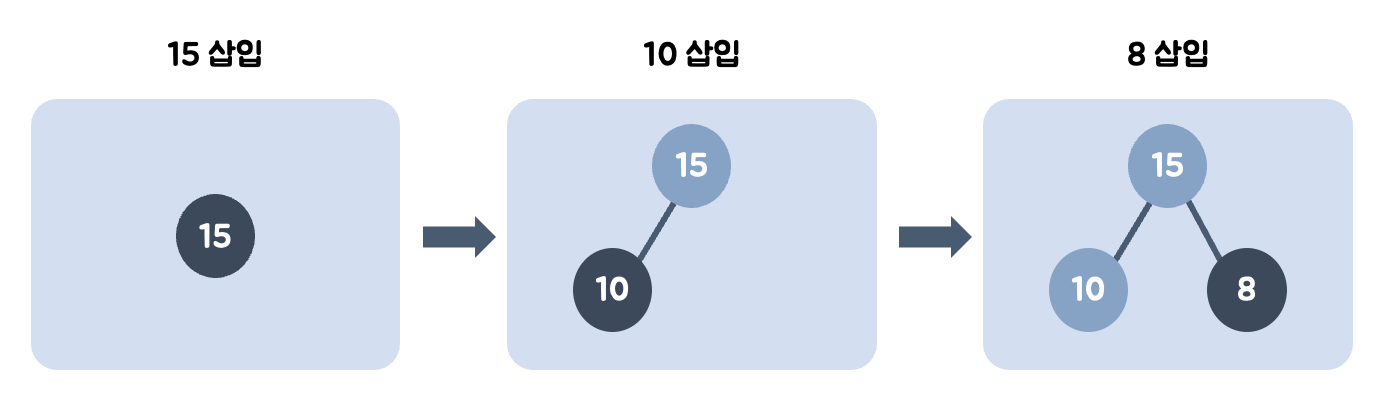
15를 왼쪽 최하단 노드에 삽입한다.
10을 왼쪽 최하단 노드에 삽입한 뒤, 부모와 비교한다. 부모보다 작으므로 그 자리에 위치한다.
왼쪽 최하단 노드가 이미 있으므로 8을 오른쪽 최하단 노드에 삽입한 뒤, 부모와 비교한다. 부모보다 작으므로 그 자리에 위치한다.

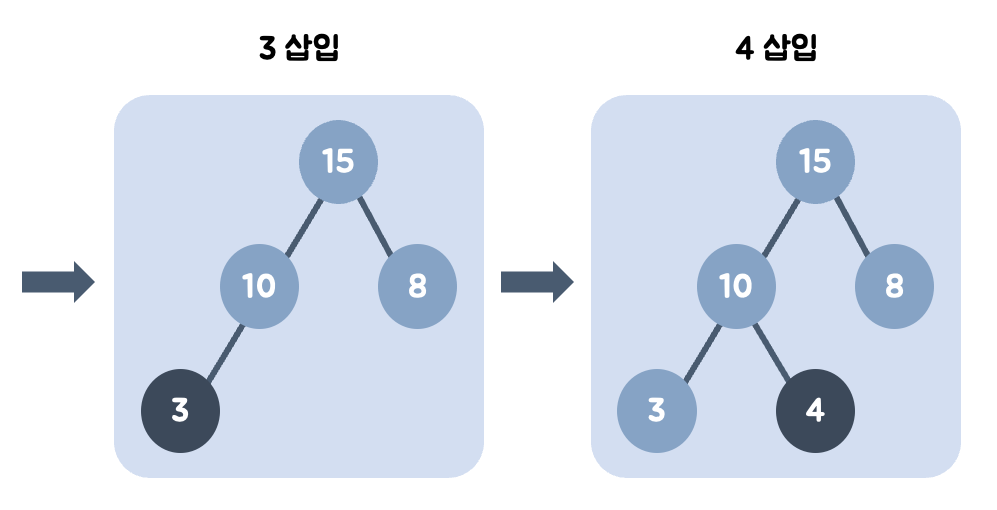
3을 왼쪽 최하단 노드에 삽입한 뒤, 부모와 비교한다. 모보다 작으므로 그 자리에 위치한다.
왼쪽 최하단 노드가 이미 있으므로 4를 오른쪽 최하단 노드에 삽입한 뒤, 부모와 비교한다. 부모보다 작으므로 그 자리에 위치한다.

데이터 삽입 (힙의 데이터보다 클 경우)

기본적으로 앞에서 설명한대로, 완전 이진 트리의 구조에 맞춰 최하단부 노드부터 채워진다.
채워진 노드의 위치에서, 부모 노드의 값보다 클 경우에는 부모 노드와 위치를 바꾸며 이를 반복한다.

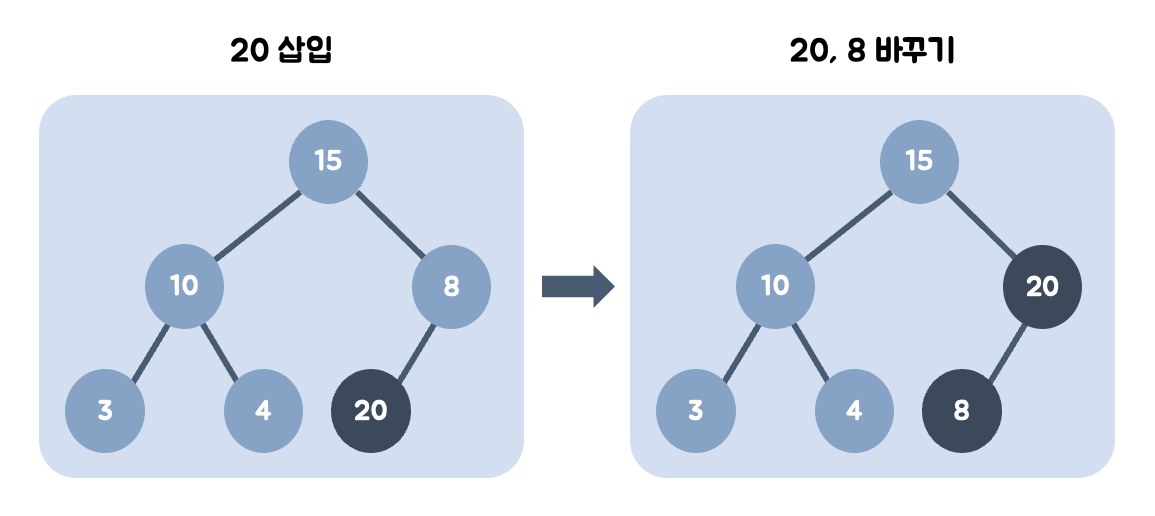
20을 왼쪽 최하단부 노드에 삽입한다.
20의 부모 노드인 8과 비교한다. 20이 더 크므로 8과 위치를 바꾼다. (swap)

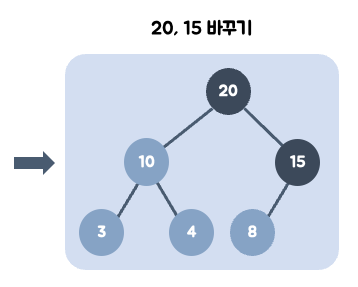
20의 부모 노드인 15와 비교한다. 20이 더 크므로 15와 위치를 바꾼다. (swap)

데이터 삭제

힙 자료구조의 목표는 바로 최대값이나 최소값을 알아내는 것이다.
때문에 데이터가 삭제 된다면 가장 큰 값인 부모 노드의 값이 삭제된다.

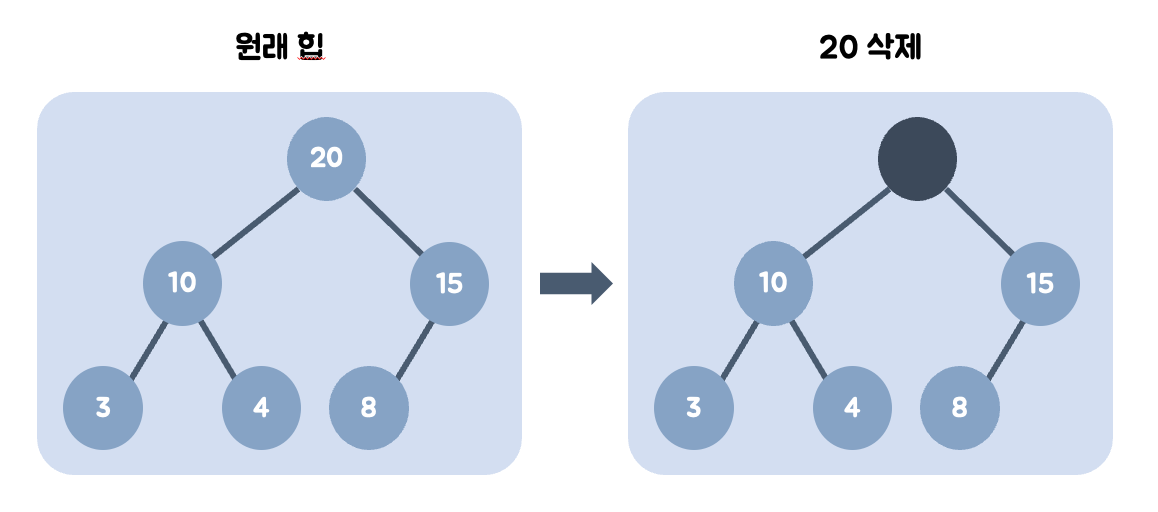
최대값을 갖는 부모 노드를 삭제한다.

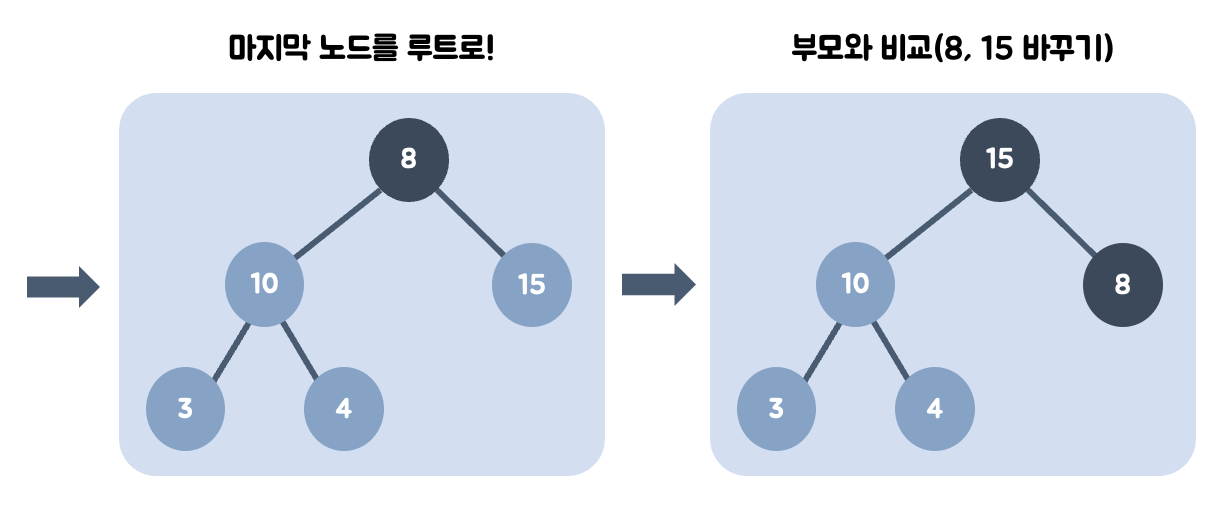
• 부모 노드가 비었으므로, 가장 최하단부 노드를 루트로 옮긴다.
  부모 노드인 8보다 값이 큰 자식 노드가 있는지 비교한다.
  
  
  • 왼쪽, 오른쪽 자식 노드 모두 부모 노드보다 클 경우
    왼쪽 자식 노드와 오른쪽 자식 노드를 비교하여, 더 큰 자식 노드와 부모 노드의 위치를 바꾼다.
    
    
  • 왼쪽, 오른쪽 자식 노드 중 하나만 부모 노드보다 클 경우
    둘 중에 부모 노드보다 큰 자식 노드와 부모 노드의 위치를 바꾼다.

출처
https://velog.io/@gnwjd309/data-structure-heap
https://heytech.tistory.com/