https://www.acmicpc.net/problem/3163
시간 1초, 메모리 256MB
input :
- 테스트케이스의 수 T
- N L k (3 ≤ N ≤ 100,000, 10 ≤ L ≤ 5,000,000, 1 ≤ k ≤ N)
- pi ai (1 ≤ pi ≤ L-1)(1 <= ai <= 10^9)
output :
- 각 테스트 케이스마다, N마리 개미 중에서 k번째로 떨어지는 개미의 ID를 출력
조건 :
-
모든 개미는 동일한 속도 초속 1mm로 이동
-
두 개미가 한 점에서 충돌하는 경우가 발생, 이 경우에 두 개미는 행진하는 방향을 반대 방향으로 바꾸고, 행진을 계속
-
개미가 막대의 끝에 도착하는 경우에는, 막대에서 떨어지게 된다.
-
두 개미가 막대 위의 한 점에 같이 있는 경우는 없다
개미가 동일한 점에서 만난다. => 이동하다가 만난다.
가장 좋은 점은 몇 칸 이동했을 때 충돌이 발생하는 지 몰라도 된다.
어차피 중앙으로 이동해서 부딪히는 놈들은 방향을 통해 알 수 있기 때문이다.
그림을 통해서 본다면 어떻게 움직이는 지 알 수 있다.
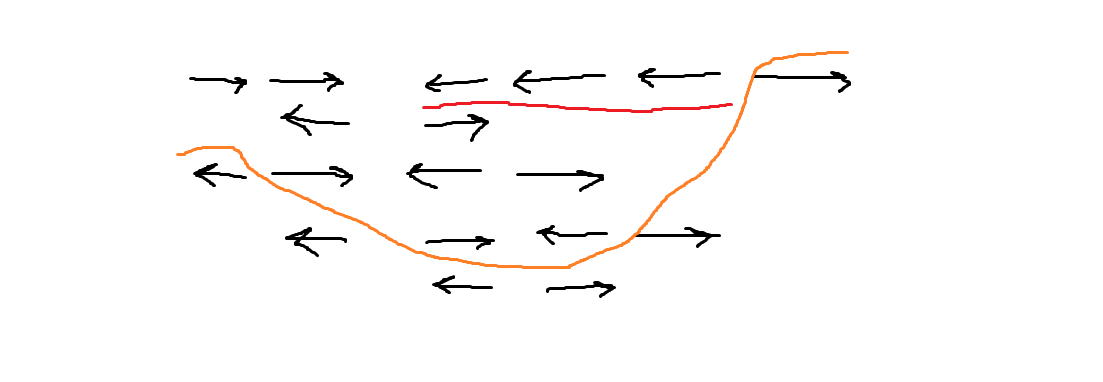
개미가 움직이는 방향의 변화를 알 수 있다. 결국 초기의 개미의 방향에 따라 왼쪽으로 가던 놈들의 수만큼 왼쪽으로 떨어진다. 그 외는 오른쪽으로 떨어지게 된다.
초반의 방향은 해당하는 방향으로 떨어지는 개미를 나타낸다.
떨어지는 순서를 구하는 방법도 위와 비슷하다. 방향이 바뀐다고는 하지만 결국 왼쪽에 제일 처음 떨어지는 놈이 이동한 거리는 ID가 음수인 애들중 첫 번째 놈이다. 2번째는 그 중 두 번째일 것이다.
왼쪽으로 이동하는 놈들은 오름차순, 오른쪽으로 이동하는 놈들은 내림차순으로 정렬하면 이동거리를 알 수 있다.
해당하는 풀이를 생각하기 위해서는 ID를 교체한다는 판단이 매우 유용하다.
ID의 변화 순서
충돌 0 : +4 +5 -1 -3 -2 +6
충돌 1 : +4 -1 +5 -3 -2 +6
충돌 2 : -1 +4 -3 +5 -2 +6
충돌 3 : -1 -3 +4 -2 +5 +6
충돌 4 : -1 -3 -2 +4 +5 +6
의 형태를 가지게 된다.
다른 분들의 풀이를 보면 초기에 충돌이 없다고 가정을 하고 문제를 우선 이해하는 경우가 있었는데 이와 비슷한 것 같다.
다음 풀이
- 막대의 끝에서 떨어짐
- 동일한 점에서 충돌
- ID가 존재
막대의 끝에서 한칸 더 이동해야 떨어진다.
동일한 점에서 충돌하는 것은 정수의 위치가 아니어도 가능하다.
ID는 유지해야 한다. 충돌하는 것을 손으로 그려보는 것은 유용하다.
투 포인터와 비슷한 모양새를 띄고 있기 때문에 충돌의 결과를 알 수만 있다면 빠른 접근이 가능할 것 같다.
import sys
t = int(sys.stdin.readline())
for _ in range(t):
n, l, k = map(int, sys.stdin.readline().split())
ids, left, right = [], [], []
for i in range(n):
p, a = map(int, sys.stdin.readline().split())
ids.append(a)
if a > 0:
dist = l - p + 1
right.append(dist)
else:
dist = p + 1
left.append(dist)
right.sort(reverse=True)
left.sort()
move = left + right
ans = [(move[i], ids[i]) for i in range(n)]
ans.sort(key=lambda x:(x[0], x[1]))
print(ans[k - 1][1])

