부동소수점과 BigDecimal

1. 실수의 표현 방식

컴퓨터에서 실수를 표현하는 방식은 정수에 비해 훨씬 복잡하다. 왜냐하면, 컴퓨터에서는 실수를 정수와 마찬가지로 2진수로만 표현해야 되기 때문이다. 따라서 실수를 표현하기 위한 다음과 같은 방법들이 연구되었으며, 현재에는 다음과 같은 방식이 사용되고 있다.

1. 고정 소수점(fixed point) 방식
2. 부동 소수점(floating point) 방식

2. 고정 소수점(fixed point) 방식

실수는 보통 정수부와 소수부로 나눌 수 있다. 따라서 실수를 표현하는 가장 간단한 방식은 소수의 자릿수를 미리 정하여, 고정된 자리의 소수를 표현하는 것이다.

32비트 실수를 고정 소수점 방식으로 표현하면 다음과 같다.

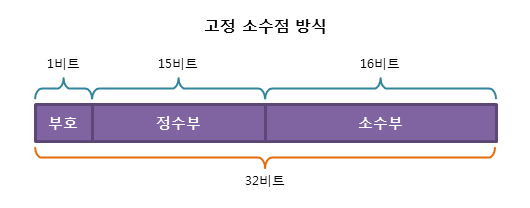
하지만 이 방식은 정수부와 소수부의 차이가 크지 않으므로, 표현할 수 있는 범위가 매우 적다는 단점이 있다.

3. 부동 소수점(floating point) 방식

실수는 보통 정수부와 소수부로 나누지만, 가수부와 지수부로 나누어 표현할 수도 있다. 부동 소수점 방식은 이렇게 하나의 실수를 가수부와 지수부로 나누어 표현하는 방식이다.

앞서 살펴본 고정 소수점 방식은 제한된 자릿수로 인해 표현할 수 있는 범위가 매우 작았다. 하지만 부동 소수점 방식은 다음 수식을 이용하여 매우 큰 실수까지도 표현할 수 있다.

현대 대부분의 시스템에서는 부동 소수점 방식으로 실수를 표현하고 있다.

4. IEEE 부동 소수점 방식

현재 사용되고 있는 부동 소수점은 대부분 IEEE 754 표준을 따르고 있다. 32비트의 float형 실수를 IEEE 부동 소수점 방식으로 표현하면 다음과 같다.

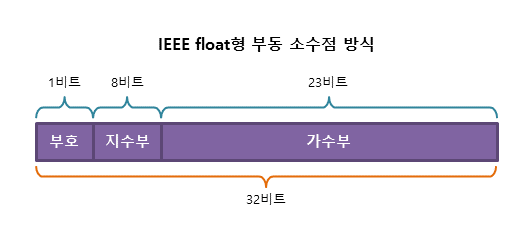
64비트의 double형 실수를 IEEE 부동 소수점 방식으로 표현하면 다음과 같다.

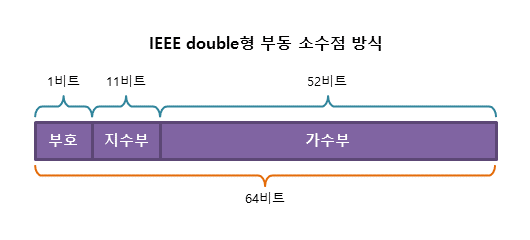
5. 부동 소수점 방식의 오차

부동 소수점 방식을 사용하면 고정 소수점 방식보다 훨씬 더 많은 범위까지 표현할 수 있다. 하지만 부동 소수점 방식에 의한 실수의 표현은 항상 오차가 존재한다는 단점을 가지고 있다.

부동 소수점 방식에서의 오차는 앞서 살펴본 공식에 의해 발생한다. 이 공식을 사용하면 표현할 수 있는 범위는 늘어나지만, 10진수를 정확하게 표현할 수는 없게 된다. 따라서 컴퓨터에서 실수를 표현하는 방법은 정확한 표현이 아닌 언제나 근사치를 표현할 뿐이다.

다음 예제는 부동 소수점 방식으로 실수를 표현할 때 발생할 수 있는 오차를 보여주는 예제이다.

double num = 0.1;
for(int i = 0; i < 1000; i++){
    num += 0.1;
}
System.out.println(num);

100.09999999999859

위의 예제에서 0.1을 1000번 더한 합계는 100이 되어야 하지만, 실제로는 100.09999999999859가 출력된다.

이처럼 컴퓨터에서 실수를 가지고 수행하는 모든 연산에는 언제나 작은 오차가 존재하게 된다. 이것은 자바 뿐만 아니라 모든 프로그래밍 언어에서 발생하는 기본적인 문제이다.

다음 예제는 자바의 실수형 타입인 double형과 float형이 표현할 수 있는 정밀도를 표현하는 예제이다.

float num3 = 1.23456789f;
		double num4 = 1.23456789;

		System.out.println("float형 변수 num3 : " + num3);
		System.out.println("double형 변수 num4 : " + num4);

float형 변수 num3 : 1.2345679
double형 변수 num4 : 1.23456789

위의 예제는 float형 타입이 소수 부분 6자리까지는 정확하게 표현할 수 있으나, 그 이상은 정확하게 표현하지 못함을 보여준다. 자바의 double형 타입은 소수 부분 15자리까지 오차없이 표현할 수 있다. 하지만 그 이상의 소수 부분을 표현할 때는 언제나 작은 오차가 발생하게 된다.

6. BigInteger 클래스

정수형으로 표현할 수 있는 값에는 한계가 있다. 가장 큰 정수형 타입인 long으로 표현할 수 있는 값은 10진수로 19자리 정도이다. 이 값도 상당히 큰 값이지만, 과학적 계산에서는 더 큰 값을 다뤄야 할 때가 있다. 그럴 때 사용하면 좋은 것이 바로 BigInteger이다. BigInteger는 내부적으로 int 배열을 사용해서 값을 다룬다. 그래서 long 타입보다 훨씬 큰 값을 다룰 수 있는 것이다. 대신 성능은 long 타입보다 떨어질 수 밖에 없다.

final int signum;	// 부호. 1(양수), 0, -1(음수) 셋 중의 하나
final int[] mag;	// 값(magnitude)

위의 코드에서 알 수 있듯이, BigInteger는 String처럼 불변(immutable)하다.(final 키워드) 그리고 모든 정수형이 그렇듯이, BigInteger 역시 값을 2의 보수 형태로 표현한다.

좀 더 자세히 말하면, 위의 코드에서 알 수 있듯이 부호를 따로 저장하고 배열에는 값 자체만 저장한다. 그래서 signum의 값이 -1, 즉 음수인 경우, 2의 보수법에 맞게 mag의 값을 변환해서 처리한다. 그래서 부호만 다른 두 값의 mag는 같고 signum은 다르다.

BigInteger의 생성

BigInteger의 생성하는 방법은 여러 가지가 있는데, 문자열로 숫자를 표현하는 것이 일반적이다. 정수형 리터럴로는 표현할 수 있는 값의 한계가 있기 때문이다.

BigInteger val;
val1 = new BigInteger("12345678901234567890");	//문자열로 생성
val2 = new BigInteger("FFFF", 16); // n진수(radix)의 문자열로 생성
val = BigInteger.valueOf(1234567890L); // 숫자로 생성

다른 타입으로 변환

BigInteger를 문자열, 또는 byte 배열로 변환하는 메서드는 다음과 같다.

String toString()		// 문자열로 변환
String toString(int radix)	// 지정된 진법(radix)의 문자열로 변환
byte[] toByteArray()	// byte 배열로 변환

BigInteger도 Number부터 상속받은 기본형으로 변환하는 메서드들을 가지고 있다.

int 	intValue()
long	longValue()
float	floatValue()
double	doubleValue()

정수형으로 변환하는 메서드 중에서 이름 끝에 "Exact"가 붙은 것은 변환한 결과가 변환된 타입의 범위에 속하지 않으면 "ArithmeticException"을 발생시킨다.

byte byteValueExact()
int intValueExact()
long longValueExact()

BigInteger의 연산

BigInteger에는 정수형에 사용할 수 있는 모든 연산자와 수학적인 계산을 쉽게 해주는 메서드들이 정의되어 있다. 기본적인 연산을 수행하는 메서드 몇 개만 고르면 아래와 같다.

BigIntger add(BigInteger val)		// 덧셈(this + val)
BigIntger substract(BigIntger val)	// 뺄셈(this - val)
BigIntger multiply(BigIntger val)	// 곱셈(this * val)
BigIntger divide(BigInteger val)	// 나눗셈(this / val)
BigIntger remainder(BigIntger val)	// 나머지(this % val)

참고로 remainder와 mod는 둘 다 나머지를 구하는 메서드지만, mod는 나누는 값이 음수면 ArithmethicException을 발생시킨다는 점이 다르다.

BigInteger는 불변이므로, 반환타입이 BigIntger라는 얘기는 새로운 인스턴스가 반환된다는 뜻이다.

비트 연산 메서드

워낙 큰 숫자를 다루기 위한 클래스이므로, 성능을 향상시키기 위해 비트단위로 연산을 수행하는 메서드들을 많이 다루고 있다. and, or, xor, not과 같이 비트연산자를 구현한 메서드들은 물론이고 다음과 같은 메서드들도 제공한다.

int binCount()	// 2진수로 표현했을 때, 1의 개수(음수는 0의 개수를 반환)
int bitLength()	// 2진수로 표현했을 때, 값을 표현하는데 필요한 bit의 개수
boolean testBit(int n)	// 우측에서 n+1번째 비트가 1이면 true, 0이면 false
BigInteger setBit(int n) // 우측에서 n+1번째 비트를 1로 변경
BigInteger clearBit(int n) // 우측에서 n+1번째 비트를 0으로 변경
BigIntger flipBit(int n) // 우측에서 n+1번째 비트를 전환(1->0, 0->1)

BigIntger의 경우 짝수인지 확인할 때, 2로 나머지 연산한 결과가 0인지 확인하는 식을 작성하면 다음과 같다.

BigInteger bi = new BigInteger("4");
if(bi.remainder(new BigInteger("2)).equals(BigInteger.ZERO)) {
	'''
}

대신 짝수는 제일 오른쪽 비트가 0일 것이므로, testBit(0)으로 마지막 비트를 확인하는 것이 더 효율적이다.

BigInteger bi = new BigIntger("4");
if(!bi.testBi(0)) {
    '''
}

이처럼, 가능하면 산술연산 대신 비트연산으로 처리하도록 노력해야 한다.

package com.company;

import java.math.*;
public class BigIntgerEx {
    public static void main(String[] args) throws Exception{
        for(int i = 1; i < 100; i++){   //1!부터 99!까지 출력
            System.out.printf("%d!=%s%n", i, calcFacorial(i));
            Thread.sleep(300);  //0.3초의 지연
        }
    }
    static String calcFacorial(int n){
        return factorial(BigInteger.valueOf(n)).toString();
    }

    static BigInteger factorial(BigInteger n){
        if(n.equals(BigInteger.ZERO))
            return BigInteger.ONE;
        else    //return n * factorial(n-1);
            return n.multiply(factorial(n.subtract(BigInteger.ONE)));
    }
}

1!~99!까지 출력하는 예제이다. long 타입으로는 20!까지밖에 계산할 수 없지만, BigInteger 타입으로는 99!까지, 그 이상도 얼마든지 가능하다. BigInteger의 최대값은 ±2의 Intger.MAX_VALUE제곱인데, 10진수로는 10의 60억 제곱이다.

// 6.464569929448805E8
System.out.println(Math.log10(2) * Integer.MAX_VALUE);

7. BigDecimal 클래스

위의 float 형 타입은 소수 6자리까지밖에 정확하게 표현할 수 없으며, double 형 타입은 소수 15자리까지 정확하게 표현할 수 없기 때문에 실수형의 특성상 오차를 피할 수 없다. BigDecimal은 실수형과 달리 정수를 이용해서 실수를 표현한다. 실수의 오차는 10진 실수를 2진 실수로 정확히 변환할 수 없는 경우가 있기 때문에 발생하는 것이므로, 오차가 없는 10진 정수로 변환하여 다루는 것이다. 실수를 정수와 10의 제곱의 곱으로 표현한다.

정수 × 10^(-scale)

scale은 0부터 Integer.MAX_VALUE사이의 범위에 있는 값이다. 그리고 BigDecimal은 정수를 저장하는데 BigInteger를 사용한다. 참고로 BigDecimal도 BigInteger처럼 불변(immutable)이다.

private final BigInteger intVal; //정수(unscaled value)
private final int scale; // 지수(scale)
private transient int precision; // 정밀도(precision) - 정수의 자릿수

예를 들어 123.45는 12345 * 10^(-2)로 표현할 수 있으며, 이 값이 BigDecimal에 저장되면 intVal의 값은 12345가 되며 scale의 값은 2가 된다. 그리고 precision의 값은 5가 되는데, 이 값은 정수의 전체 자리수를 의미한다.

BigIntger val = new BigInteger("123.45"); // 12345 * 10^(-2)
System.out.println(val.unscalabledValue()); // 12345
System.out.println(val.scale());  // 2
System.out.println(val.precision());  // 5

BigDecimal의 생성

BigDecimal를 생성하는 방법은 여러 가지가 있는데, 문자열로 숫자를 표현하는 것이 일반적이다. 기본형 리터럴로는 표현할 수 있는 값의 한계가 있기 때문이다.

BigDecimal val;
val = new BigDecimal("123.4567890"); // 문자열로 생성
val = new BigDecimal(123.456); // double 타입의 리터럴로 생성
val = new BigDecimal(123456); // int, long 타입의 리터럴로 생성가능
val = BigDecimal.valueOf(123.456); // 생성자 대신 valueOf(double) 사용
val = BigDecimal.valueOf(123456); // 생성자 대신 valueOf(int) 사용

그리고 한 가지 주의할 점은, double 타입의 값을 매개변수로 갖는 생성자를 사용하면 오차가 발생할 수 있다는 것이다.

System.out.println(new BigDecimal(0.1)); 
// 0.1000000000000000055511151231257827021181583404541015625
System.out.println(new BigDecimal("0.1"));
// 0.1

다른 타입으로의 변환

BigDecimal을 문자열로 변환하는 메서드는 다음과 같다.

String toPlainString() // 어떤 경우에도 다른 기호없이 숫자로만 표현
String toString() // 필요하면 지수형태로도 표현할 수 있음

대부분의 경우 이 두 메서드의 반환결과가 같지만, BigDecimal을 생성할 때 '1.0e-22'와 같은 지수형태의 리터럴을 사용했을 때 다른 결과를 얻는 경우가 있다.

BigDecimal val = new BigDecimal(1.0e-22);
System.out.println(val.toPlainString());
// 0.00000000000000000000010000000000000000485967743265708723529783189783450120951502847720104849571498561999760568141937255859375
System.out.println(val.toString());
// 1.0000000000000000485967743265708723529783189783450120951502847720104849571498561999760568141937255859375E-22

BigDecimal도 Number로 부터 상속받은 기본형으로 변환하는 메서드들을 가지고 있다.

int intValue()
long longValue()
float floatValue()
double doubleValue()

BigDecimal을 정수형으로 변환하는 메서드 중에서 이름 끝에 "Exact"가 붙은 것들은 반환한 결과가 변환한 타입의 범위에 속하지 않으면 ArithmeticException을 발생시킨다.

byte byteValueExact()
short shortValueExact()
int intValueExact()
long longValueExact()
BigInteger toBigIntgerExact()

BigDecimal의 연산

BigDecimal에는 실수형에 사용할 수 있는 모든 연산자와 수학적인 계산을 쉽게 해주는 메서드들이 정의되어 있다. 아래는 기본적인 연산을 수행하는 메서드 몇 개만 골라보면 아래와 같다.

BigDecimal add(BigDecimal val) // 덧셈(this + val)
BigDecimal substract(BigDecimal val) // 뺄셈(this - val)
BigDecimal multiply(BigDecimal val) // 곱셈(this * val)
BigDecimal divide(BigDecimal val) // 나눗셈(this / val)
BigDecimal remainder(BigDecimal mal) // 나머지(this % val)

BigInteger와 마찬가지로 BigDecimal은 불변이므로, 반환타입이 BigDecimal인 경우 새로운 인스턴스가 반환된다.

한 가지 알아둬야 할 것은 연산결과의 정수, 지수, 정밀도가 달라진다는 것이다.

						//value, scale, precision
BigDecimal bd1 = new BigDecimal("123.456");     //123456,   3,      6
BigDecimal bd2 = new BigDecimal("1.0);	        //10,       1,      2
BigDecimal bd3 = bd.multiply(bd2);		//1234560,  4,      7		

곱셈에서는 두 피연산자의 scale을 더하고, 나눗셈에서는 뺀다. 덧셈과 뺄셈에서는 둘 중에서 자리수가 높은 쪽으로 맞추기 위해서 두 scale 중에서 큰 쪽이 결과가 된다.

반올림 모드 - divide()와 setScale()

다른 연산과 달리 나눗셈을 처리하기 위한 메서드는 다음과 같이 다양한 버전이 존재한다. 나눗셈의 결과를 어떻게 반올림(roundingMode) 처리할 것인가와, 몇 번째 자리(scale)에서 반올림할 것인지를 지정할 수 있다. BigDecimal이 아무런 오차없이 실수를 저장한다 해도 나눗셈에서 발생하는 오차는 어쩔 수 없다.

BigDeciaml divide(BigDecimal divisor)
BigDecimal divide(BigDecimal divisor, int roundingMode)
BigDecimal divide(BigDeciaml divisor, RoundingMode roundingMode)
BigDecimal divie(BigDecimal divisor, int scale, int roundingMode)
BigDecimal divide(BigDecimal divisor, int scale, RoundingMode roundingMode)
BigDecimal divide(BigDecimal divisor, MathContext mc)

roundingMode는 반올림 처리방법에 대한 것으로 BigDecimal에 정의된 'ROUND_'로 시작하는 상수들 중에 하나를 선택해서 사용하면 된다. RoundingMode는 이 상수들을 열거형으로 정의한 것으로 나중에 추가되었다. 가능하면 열거형 RoundingMode를 사용하자.

상수	설명
CELING	올림
FLOOR	내림
UP	양수일 때는 올림, 음수일 때는 내림
DOWN	양수일 때는 내림, 음수일 때는 올림(UP과 반대)
HALF_UP	반올림(5이상 올림, 5미만 버림)
HALF_EVEN	반올림(반올림 자리의 값이 짝수면 HALF_DOWN, 홀수면 HALF_UP)
HALF_DOWN	반올림(6이상 올림, 6미만 버림)
UNNECESSARY	나눗셈의 결과가 딱 떨어지는 수가 아니면, ArithmeticException발생

주의해야 할 점은 1.0 / 3.0처럼 divide()로 나눗셈한 결과가 무한소수인 경우, 반올림 모드를 지정하지 않으면 ArithmeticException이 발생한다는 것이다.

BigDecimal bigd = new BigDecimal("1.0");
BigDecimal bigd2 = new BigDecimal("3.0");

System.out.println(bigd.divide(bigd2)); // ArithmeticException 발생
System.out.println(bigd.divide(bigd2, 3, RoundingMode.HALF_UP)); //0.333

java.math.MathContext

이 클래스는 반올림 모드와 정밀도(precision)을 하나로 묶어 놓은 것일 뿐 별다른 것은 없다. 한 가지 주의할 점은 divide()에서는 scale이 소수점 이하의 자리수를 의미하는데, MathContext에서는 precision이 정수와 소수점 이하를 모두 포함한 자리수를 의미한다는 것이다.

BigDecimal bd1 = new BigDecimal("123.456");
BigDecimal bd2 = new BigDecimal("1.0");

System.out.println(bd1.divide(bd2, 2, RoundingMode.HALF_UP)); //123.46
System.out.println(bd1.divide(bd2, new MathContext(2, RoundingMode.HALF_UP))); //1.2E+2

그래서 위의 결과를 보면, scale이 2이면 나눗셈의 결과가 소수점 두 자리까지 출력되는데, MathContext를 이용한 결과는 precision을 가지고 반올림 하므로 bd1의 precision인 12346에서 세 번째 자리에서 반올림해서 precision은 12000이 아니라 12가 된다. 여기에 scale이 반영되어 '1.2E+2'가 된 것이다.

scale의 변경

BigDecimal을 10으로 곱하거나 나누는 대신 scale의 값을 변경함으로써 같은 결과를 얻을 수 있다. BigDecimal의 scale을 변경하려면, setScale()을 이용하면 된다.

BigDecimal setScale(int newScale);
BigDecimal setScale(int newScale, int roundingMode);
BigDecimal setScale(int newScale, RoundingMode mode);

setScale()로 scale 값을 줄이는 것은 10의 n 제곱으로 나누는 것과 같으므로, divide()를 호출할 때처럼 오차가 발생할 수 있고 반올림 모드를 지정할 수 있다.

import java.math.BigDecimal;
import java.math.MathContext;
import java.math.RoundingMode;

public class BigDecimalEx {
    public static void main(String[] args){
        BigDecimal bd1 = new BigDecimal("123.456");
        BigDecimal bd2 = new BigDecimal("1.0");

        System.out.print("bd1="+bd1);
        System.out.print(",\tvalue="+bd1.unscaledValue());
        System.out.print(",\tscale="+bd1.scale());
        System.out.print(",\tprecision="+bd1.precision());
        System.out.println();

        System.out.print("bd2="+bd2);
        System.out.print(",\tvalue="+bd2.unscaledValue());
        System.out.print(",\tscale="+bd2.scale());
        System.out.print(",\tprecision="+bd2.precision());
        System.out.println();

        BigDecimal bd3 = bd1.multiply(bd2);
        System.out.print("bd3="+bd3);
        System.out.print(",\tvalue="+bd3.unscaledValue());
        System.out.print(",\tscale="+bd3.scale());
        System.out.print(",\tprecision="+bd3.precision());
        System.out.println();

        System.out.println(bd1.divide(bd2, 2, RoundingMode.HALF_UP));
        System.out.println(bd1.setScale(2, RoundingMode.HALF_UP));
        System.out.println(bd1.divide(bd2, new MathContext(2, RoundingMode.HALF_UP)));
    }
}

실행 결과

bd1=123.456,	value=123456,	scale=3,	precision=6
bd2=1.0,	value=10,	scale=1,	precision=2
bd3=123.4560,	value=1234560,	scale=4,	precision=7
123.46
123.46
1.2E+2

참고

• http://www.tcpschool.com/java/java_datatype_floatingPointNumber
• https://madplay.github.io/post/the-need-for-bigdecimal-in-java
• 자바의 정석