문제

풀이

• 시작하는 수를 기준으로 DP를 작성하면 다음과 같은 점화식을 얻을 수 있다.
  

• 시작하는 수를 열 계단 수 길이를 행으로 하여 중간 결과를 작성하면 다음과 같다.

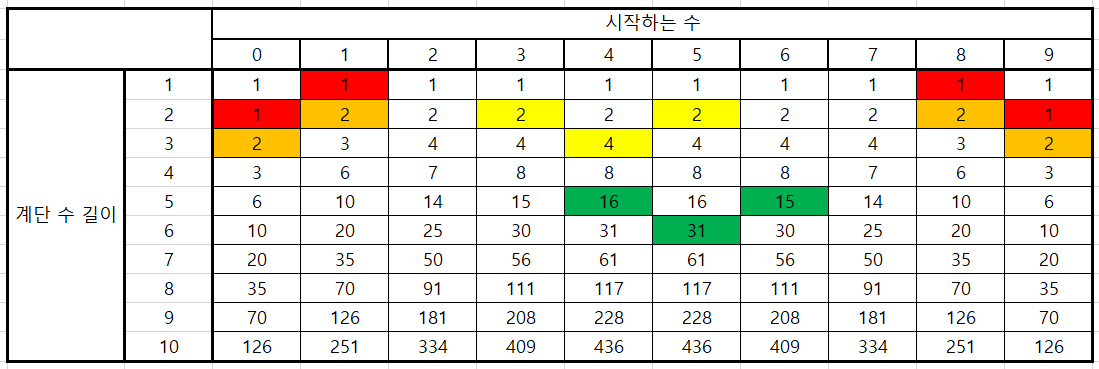
• 마지막으로 경우의 수가 매우 커질 수 있으니 항상 1,000,000,000로 나눈 나머지만을 저장해야한다. 그렇지 않으면 overflow 발생한다. 그리고 이렇게 나머지만으로도 계산이 잘 되는 이유는 어차피 경우의 수의 합이기 때문이다.

코드

//난이도 : 실버1
//시작 : 17:36 - 18:08, 21:40 -
//끝 : 22:46
#include <iostream>

using namespace std;

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N;
	cin >> N;
	//r은 계단 수 길이, c는 시작하는 번호
	long long int result[101][10] = {0}; //중간 결과를 저장할 공간
	for (int c = 0; c < 10; c++) { //1개로 만들 수 있는 경우의 수 모두 1이므로 결과 저장
		result[1][c] = 1;
	}
	for (int r = 2; r <= N; r++) {
		result[r][0] = result[r - 1][1] % 1000000000; //0으로 시작하는 번호는 그 다음 수가 1이어만 하므로 1개 적은 길이에서 1로 시작하는 경우와 같다.
		result[r][9] = result[r - 1][8] % 1000000000; //9로 시작하는 번호는 그 다음 수가 8이어만 하므로 1개 적은 길이에서 8로 시작하는 경우와 같다.
		for (int c = 1; c < 9; c++) { //1~8로 시작하는 경우에는 각각 1개 적은 길이에서 각각 크고 작은 경우를 합치면 된다.
			//결과는 1000000000로 나눈 나머지이며 저장 범위를 넘어가기에 반드시 나머지만 저장해야한다.
			result[r][c] = (result[r - 1][c - 1] + result[r - 1][c + 1]) % 1000000000;  
		}
	}

	long long int final = 0;
	for (int c = 1; c <= 9; c++) { //해당 길이에서 1~9에서 시작하는 모든 경우의 수를 합치면 되며 범위를 저장 범위를 넘을 수 있기에 1000000000의 나머지만을 취한다.
		final += result[N][c];
		final %= 1000000000;
	}
	cout << final << '\n';

	return 0;
}