정글 week01. 핵심 키워드 - 시간 복잡도, Big O Notation
복잡도(complexity)
: 알고리즘 성능을 평가하는 척도
- 시간 복잡도(time complexity): 실행하는 데 필요한 시간을 평가
: 입력된 N의 크기에 따라 실행되는 조작의 수- 공간 복잡도(space complexity): 메모리(기억 공간)과 파일 공간이 얼마나 필요한지를 평가
=> 알고리즘을 구현할 때 시간복잡도는 프로그램 최적화를 위해 필수적으로 생각해야하는 것! 어떻게 하면 더 효율적으로 구현할 수 있는지 생각해보자.

Big O notation

알고리즘의 최악의 실행 시간- 어떤 알고리즘의 시간 복잡도가
O(f(n))이라고 할 때, 이는 입력 크기 n에 대해 알고리즘이 최대f(n)만큼의 시간을 소요한다는 것을 의미합니다.
따라서 빅오 표기법은상한선을 제공
Theta notation
- 알고리즘의 평균 실행 시간
Θ(f(n))이라고 할 때, 이는 알고리즘이 입력 크기 n에 대해 대략적으로f(n)만큼의 시간을 소요한다는 것을 의미
즉, 세타 표기법은 알고리즘의 상한과 하한이 동일한 경우
Omega notation
- 알고리즘의 최선의 실행 시간
- 시간 복잡도가
Ω(f(n))이라고 할 때, 이는 알고리즘이 최소f(n)만큼의 시간을 소요한다는 것을 의미합니다. - 오메가 표기법은 하한선을 제공
Big O notation을 우리는 왜 많이 쓸까? 최악의 상황을 고려해야 하기 때문.
- Big O 표기법
: 상수항은 무시한다. 작은항은 무시하고 최고차항만 표기
시간 복잡도
- 시간 복잡도 단계 (빠른순)
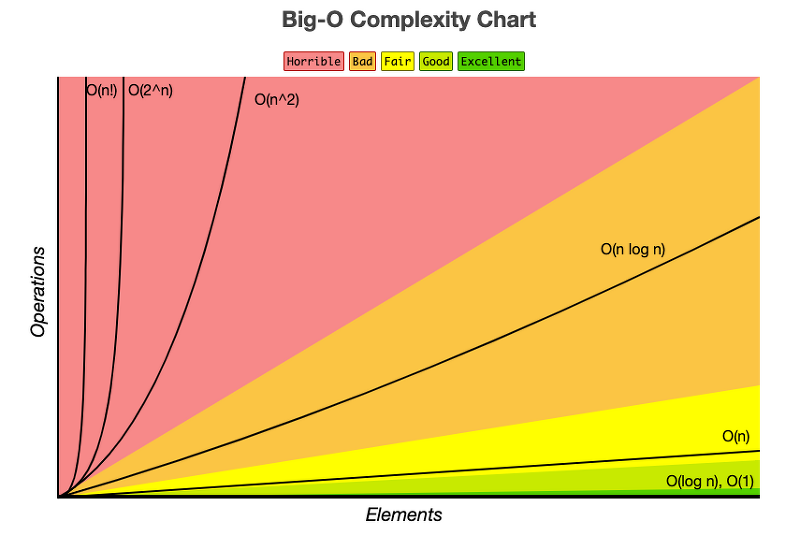
O(1) < O(logN) < O(N) < O(NlogN) < O(N^2)


O(1)- 상수 시간 복잡도:
입력값의 크기에 관계없이 항상 일정한 실행 시간이 소요즉시 출력값을 얻어낼 수 있다.
예) 배열에서 특정 인덱스의 값을 읽거나 링크드 리스트에 데이터를 삽입/제거 할 때
def hello_world():
print("Hellow world!")-
O(logN)- 로그 시간 복잡도:
입력의 크기가 커질수록 실행 시간이 로그 형태로 증가O(1) 다음으로 빠른 시간 복잡도
로그 함수처럼 입력의 크기에 따른 소요 시간의 증가율이 적음
이진 탐색 트리에서 특정 값을 찾는 경우 -
O(N)- 선형 시간 복잡도:
입력 크기에 비례하여 실행 시간이 선형으로 증가
예) 일차원 배열이나 링크드 리스트에서 특정 값을 찾는 경우, 리스트의 모든 요소를 출력하는 경우
def print_each(li):
for item in li:
print(li)-
O(NlogN)- 선형로그 시간 복잡도:
일반적으로 정렬 알고리즘 -
O(N^2)- 제곱 시간 복잡도:
입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가
이중 반복문
def print_each_n_times(li):
for n in li:
for m in li:
print(n,m)-
O(2^n)- 지수 시간:
예) 집합의 모든 부분 집합을 생성하는 예시 코드 -
O(n!)- n 팩토리얼 시간
참고)
https://blog.chulgil.me/algorithm/amp/
https://vaert.tistory.com/117
https://velog.io/@junyong92/TIL-Time-Complexity
https://m.hanbit.co.kr/channel/category/category_view.html?cms_code=CMS7965376216
https://fromnowwon.tistory.com/entry/python-bigO
*)) 각각의 자료 구조별 시간 복잡도는 어떤지,,,
탐색과 정렬할 때 시간 복잡도는 어떤지,, 추후에 추가적으로 공부할 필요가 있다.
