정글에서 0주, 1주차가 끝나고 벌써 2주차가 되었다.
1주차에서 공부했던 키워드
- 배열, 문자열
- 반복문과 재귀함수
- 복잡도(Big O, 시간, 공간)
- 정렬
- 완전탐색
- 이분탐색
- 분할정복
- 스택
- 큐
- 우선순위 큐
- Linked list
- 해시 테이블
키워드 개념은 1번씩 다 그래도 공부했지만, 코드로 구현하는 능력이 아직 매우 부족하다.정렬 특히 병합정렬과 퀵소트, 힙소트의 경우 개념은 이해갔지만 코드로 구현할 수 없기 때문에 추가적인 공부가 더 필요하다.
또한 재귀함수와 반복문! - 알고리즘 문제를 풀면서 체화시키려는 노력 필요,,
2주차 개념 키워드
- 그래프 종류/표현방식
- BFS / DFS
- 위상정렬
- B-Tree
- 트라이(Trie)
- 다익스츠라, 플로이드 와샬
- 최소신장트리
그래프
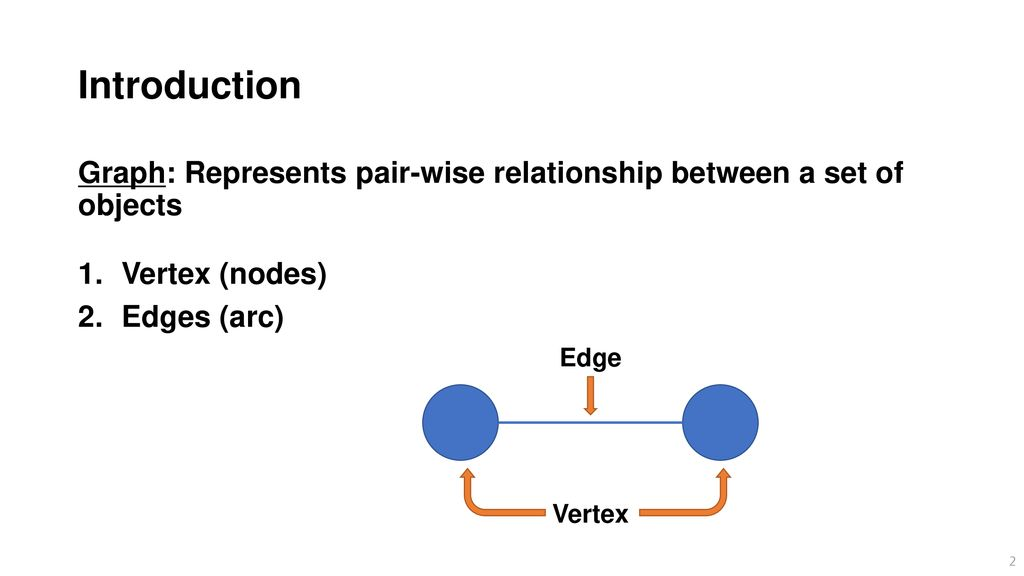
그래프?
node/vertex와edge로 표현되는 자료구조그래프의 종류
- Undirected graph
: 간선은 간선을 통해서 양방향으로 갈 수 있다.- directed graph
: 간선에 방향성이 존재(일방향)- weighted graph
: 간선에 비용이나 가중치가 할당된 그래프
그래프의 표현 방식
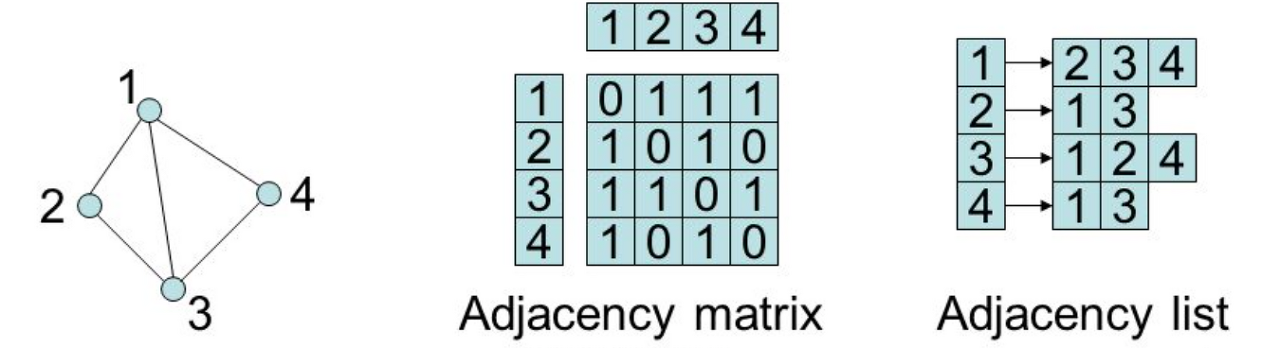
인접행렬(Adjacency Matrix)
그래프 간의 연결관계를 행렬로 -> 이차원 배열
N= 4
adj_matrix = [[0]* (N+1) for _ in range(N+1)]
edges = [
(1,2),
(1,3),
(1,4),
(2,4),
(3,4)
]
for (i,j) in edges:
adj_matrix[i][j] =1
adj_matrix[j][i] = 1
for row in adj_matrix[1:]:
print(row[1:]) #0번 인덱스는 제외 인접리스트(Adjacency List)
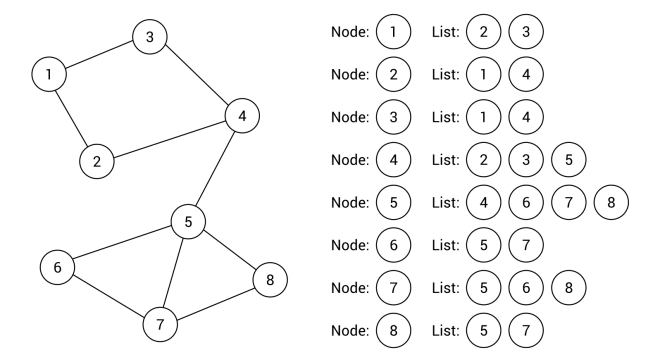
: 각각의 노드에 연결된 노드들을 원소로 갖는 리스트들의 배열
인접행렬 방식 인접리스트 방식 장/단점
전체 노드의 개수 V, 간선의 개수 E
인접행렬:
특정 간선 존재 확인: 노드i, 노드 j가 연결되어 있는지 확인하고 싶을 때, index로 접근하기 때문에O(1)의 시간 복잡도
그래프의 구조를 나타내기에 직관적
노드의 개수가 많을수록 공간 복잡도 증가
연결된 모든 노드들에 방문하고 싶은 경우 adj[i][1]부터 adj[i][V]까지 모두 확인 ->O(V)의 시간
노드의 수에 비해 간선의 개수가 훨씬 적은 그래프면 부적절
인접 리스트=> 존재하는 간선의 수만 관리 -> 메모리를 효율적으로 사용 가능
공간 복잡도가 더 효율적임.
그래프의 모든 간선을 알아내기 위해 각각의 모든 인접리스트를 탐색하여O(V+E)의 시간 복잡도
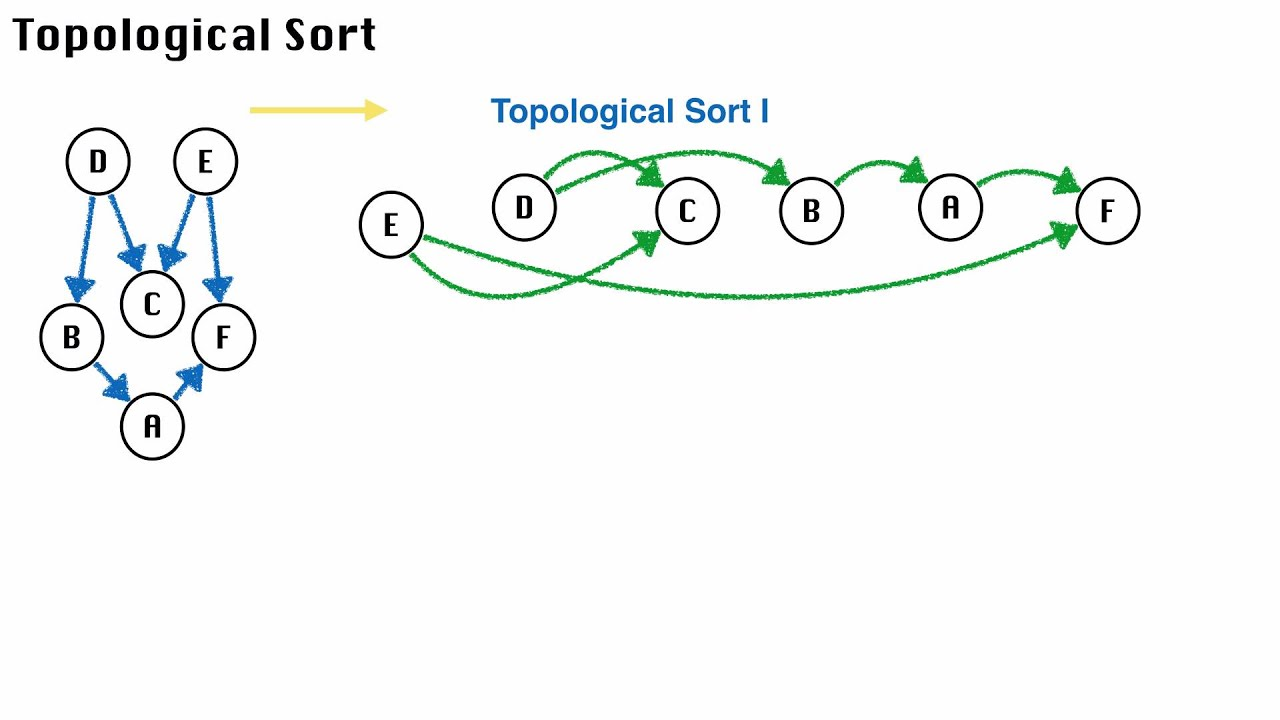
구현이 어렵다는 단점. 두 노드가 연결되었는지 확인할 때 인접행렬 방식보다 비효율적 위상정렬(topological ordering)
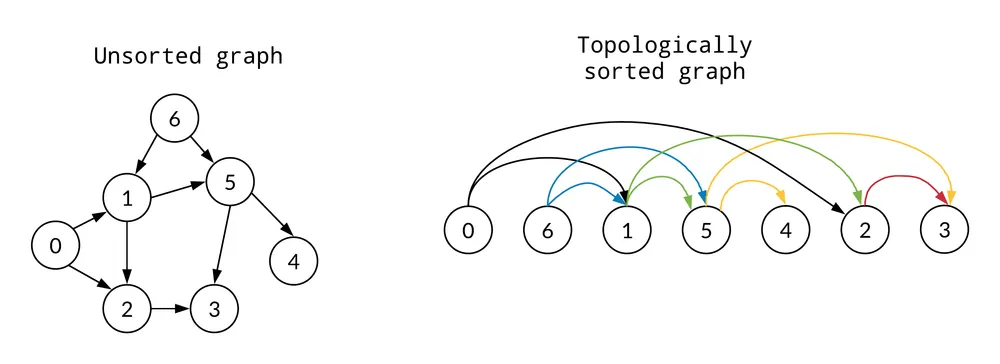
순환하지 않는 유향 그래프를 방향성에 거스르지 않도록 순서대로 배열하는 방법
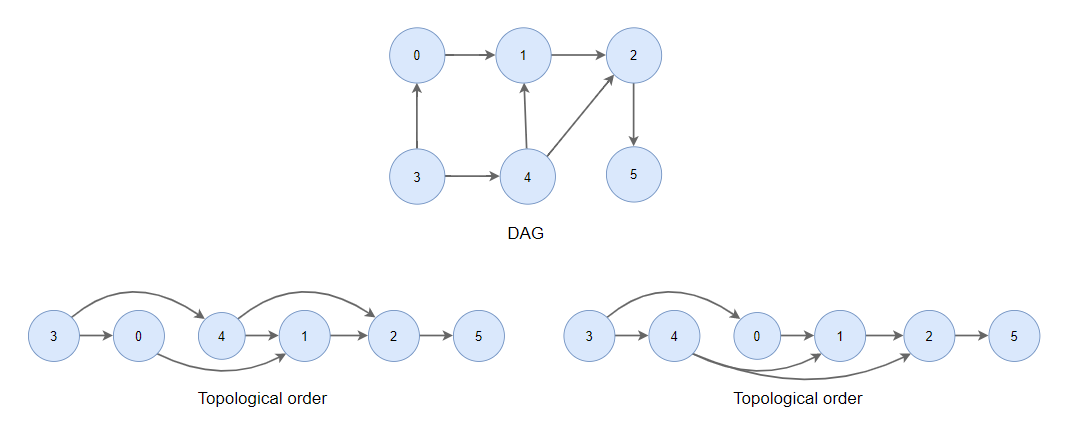
=> 그래프 내부에 순환(cycle)이 있으면 안된다. (DAG(Directed Acyclic Graph))
- 진입차수: 어떤 노드 N으로 향하는 간선의 개수
- 진출차수: 어떤 노드 N에서 다른 노드로 향하는 간선의 개수
=> 운영체제의 프로세스 스케줄링, 사이클 감지, 데이터 직렬화 등등 다양하게 활용된다.
위상정렬 알고리즘
진입 차수(In degree)가 0인 정점을 큐에 넣는다.
큐에서 정점을 하나씩 꺼내고, 해당 정점과 연결된 간선을 제거. 제거된 간선으로 정점들이 진입 차수가 감소.간선 제거 이후 진입 차수가 0인 정점을 큐에 넣는다.
큐가 빌 때까지 위의 과정을 반복합니다. 큐에서 꺼낸 순서가 정점의 위상 정렬된 결과가 된다!
- dfs를 활용할 수 있다!
dfs를 활용하면 위상정렬된 결과를 만들 수 있다.
from collections import deque
input = sys.stdin.readline
V, E = map(int, input().split())
indegree = [0] * (V+1)
graph= [[] for i in range(V+1)]
#방향 그래프
for _ in range(E):
a, b = map(int, input().split())
graph[a].append(b)
indegree[b] +=1
def topology_sort():
result = []
q = deque()
#진입차수가 0 -> 큐에 삽입
for i in range(1, V+1):
if indegree[i] ==0:
q.append(i)
while q:
now = q.popleft()
result.append(now)
for i in graph[now]:
indegree[i] -=1
if indegree[i] ==0:
q.append(i)
for i in result:
print(i)
DFS/ BFS
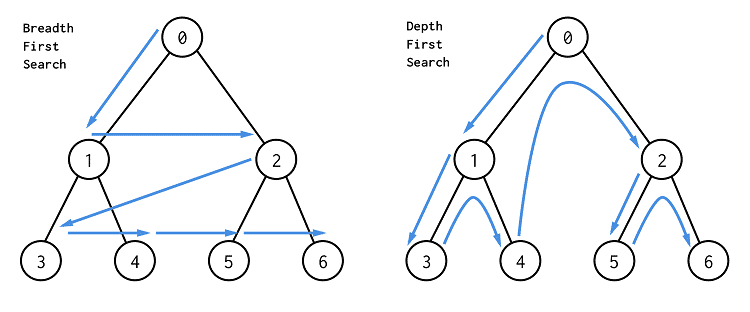
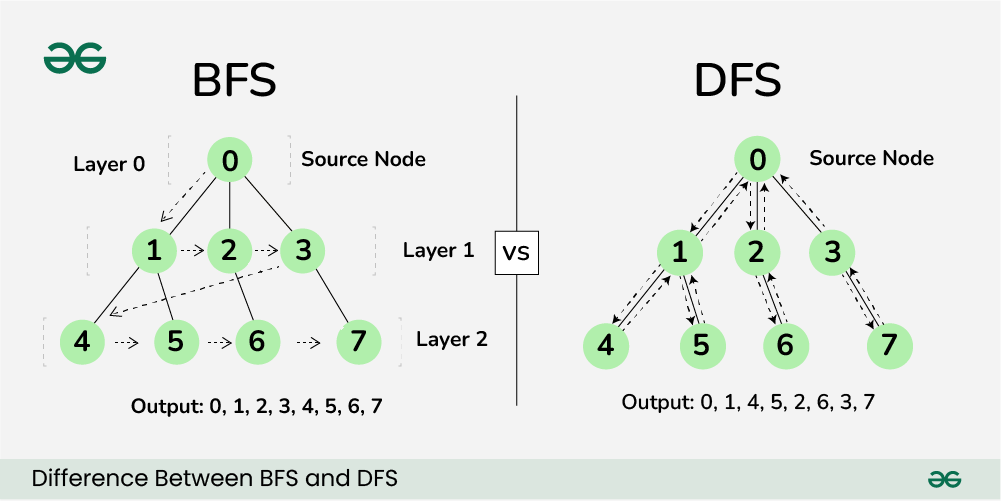
깊이 우선 탐색(Depth-First Search)
현재 정점에서 갈 수 있는 점들까지 탐색 (스택과 재귀함수)
- 장점
현 경로상의 노드들만 기억하면 되므로 저장공간 수요가 비교적 적다.
목표 노드를 찾을 때까지 최대한 깊이 들어가 탐색하므로, 더 빠르게 목표 노드에 도달할 수 있다.- 단점
해가 없는 경로가 깊을 경우 탐색 시간이 길어질 수 있다. 최단 경로를 보장하지 않는다. 미방문 노드가 많은 그래프의 경우 스택 오버플로우가 발생할 수 있다. (깊이 제한을 두면 해결이 가능하다.)def dfs(graph, v, visited): visited[v] = True print(v, end = ' ') for i in graph[v]: if not visited[i]: dfs(graph, i, visited )
너비 우선 탐색(Breadth-First Search)
현재 정점에 연결된 가까운 점들 부터 탐색 (큐)
- 장점
최단 경로를 보장 - 목표 노드와의 거리가 가까운 노드부터 탐색하기 때문에
미방문 노드의 수에 상관없이 동일한 수의 노드를 탐색한다.
최단 경로를 찾을 때 유용하다.
노드의 수가 적고 깊이가 얕은 해가 존재할 때 유리하다.- 단점
구현이 조금 더 복잡하다. 일반적인 재귀적 방식으로는 구현하기가 어렵다.
DFS보다 더 많은 메모리를 필요로 할 수 있다.from collections import deque def bfs(graph, start, visited): queue = deque([start]) visited[start] = True - while queue: v = queue.popleft() print(v, end = ' ') for i in graph[v]: if not visited[i]: queue.append(i) visited[i] = True
큐로 이해하는 BFS
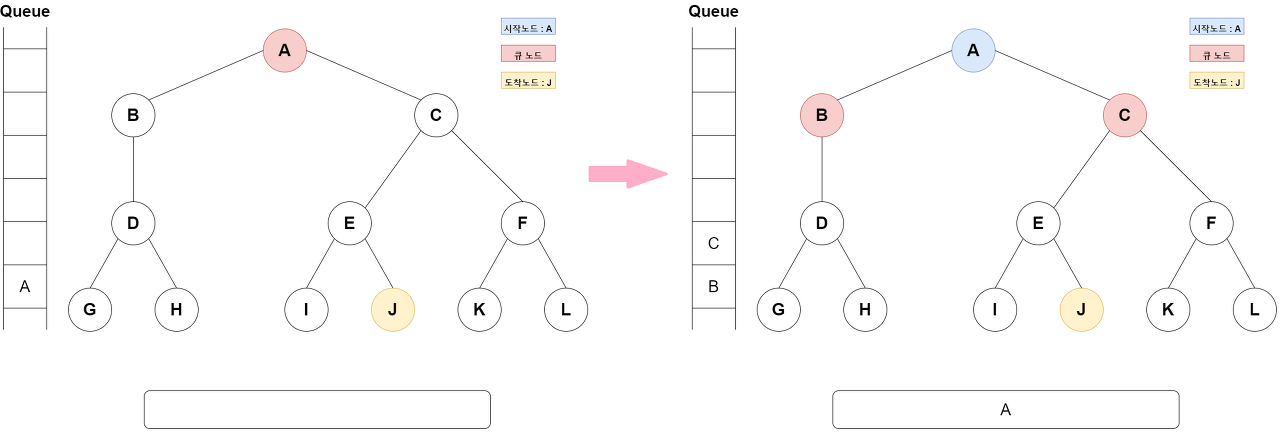
확실히 팀원들과 얘기하면서 공부하니까 더 이해가 된다. 이제 코드로 구현하는 법도 연습 열심히하자,,
근데 아직 dfs/ bfs 코드도 잘 못씀 ㅋ
참고)
https://sjkoding.tistory.com/30
https://devuna.tistory.com/32
https://currygamedev.tistory.com/10
https://velog.io/@eunchae2000/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%9E%98%ED%94%84%EB%A5%BC-%EC%A0%80%EC%9E%A5%ED%95%98%EB%8A%94-%EB%B0%A9%EB%B2%95-3%EA%B0%80%EC%A7%80-%EC%9D%B8%EC%A0%91-%ED%96%89%EB%A0%AC-%EC%9D%B8%EC%A0%91-%EB%A6%AC%EC%8A%A4%ED%8A%B8-%EA%B0%84%EC%84%A0-%EB%A6%AC%EC%8A%A4%ED%8A%B8-with-Python