[Jungle][TIL] 240416 B-Tree 삭제 | 포인터 | DP 하향식, 상향식

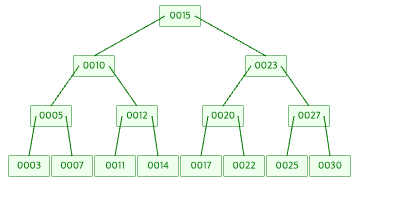
20을 삭제, LeafNode가 아닌 노드를 삭제할 경우에는 전임자(PRedecessor)와 위치를 바꾼 후 삭제하는 경우

#include <stdio.h>

void func() {
// 
}

int main() {
	int arr[5] = {1, 2, 3, 4, 5};
    func(arr, 5);
    for (int i =0; i<5; i++) {
    	printf("%d", arr[i]);
    return 0;
} 

출력값이 2 3 4 5 6이 되도록 하는 func 함수??

#include <stdio.h>

void func(int *p, int n) {
	for (int i =0; i <n; i++) {
    	*p = *p + 1;
        p++;
    }
}

int main() {
	int arr[5] = {1, 2, 3, 4, 5};
    func(arr, 5);
    for (int i =0; i<5; i++) {
    	printf("%d", arr[i]);
    return 0;
} 

*p = *p + 1
=> 포인터 p가 가리키는 현재 요소 (arr[i])에 +1 증가.
p++: 포인터 p를 다음 요소로 이동시킨다.

피보나치 수열
- DP - 상향식 접근법
아래쪽에서부터 작은 문제를 해결해나가면서 최종적으로 큰 문제의 해를 구함 -> 반복문 사용해서 구현

def fib_bottom_up(n):
	if n<=1:
    	return n
    
    //초기 피보나치 수 
    fib_0 = 0
    fib_1 = 1 
    
    for i in range(2, n+1):
    	next_fib = fib_0 + fib_1
        fib_0 = fib_1
        fib_1 = next_fib
    
    return fib_1 

• DP - 하향식 접근법
  메모이제이션을 위한 리스트 초기화

큰 문제를 작은 문제로 나누어서 작은 문제들의 해를 재귀적으로 구하고 합쳐서 큰 문제의 해를 구한다.
-> 메모이제이션 기법

def fib_top_down(n, memo=None):
	if memo is None:
    	memo = [-1] * (n+1)
    
    #기저 조건
    if n<=1:
    	return n
    
    #이미 계산된 값이면 
    if memo[n] != -1:
    	return memo[n]
    
    #재귀적으로 계산
    memo[n] = fib_top_down(n-1, memo) + fibo_top_down(n-2, memo) 
    return memo[n]