[Jungle][TIL] 240417 Binary Trees

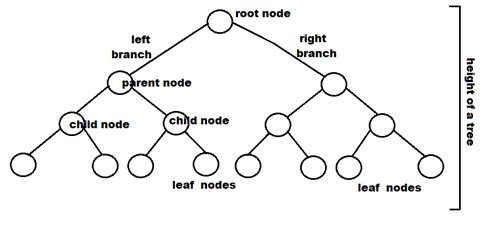
이진트리(Binary Tree)

트리 중에서도 각 노드가 최대 2개의 자식노드를 가질 때

---

int identical(BTNode *tree1, BTNode *tree2)
2개의 트리가 동일한 트리인지 판단하는 함수

{
	if (tree1 == NULL && tree2 == NULL) {
    	return1 ;
    }
    
    if (tree1 == NULL || tree2 == NULL) {
    	return 0;
    }	
    
    if (tree1 -> item != tree2 -> item) {
    	return 0;
    }
    
    if ((identical(tree1-> left, tree2-> left) && (identical(tree1-> right, tree2->right)) {
    	return 1;
    } else {
  		return 0;
    }
}

---

int maxHeight(BTNode *node)
이진 트리의 최대 높이를 구하는 함수

int maxHeight(BTNode *node) {
	if (node == NULL) {
    	return -1;
    }
    
    int leftHeight;
    leftHeight = maxHeight(node->left) ;
    int rightHeight;
    rightHeight = maxHeight(node->right);
    
    if (leftHeight >= rightHeight) {
    	return leftHeight +1 ;
    } else {
    	return rightHeight + 1 ;
    } 
 }

왼쪽 서브트리와 오른쪽 서브트리의 높이 비교
최종적으로 더 큰 값 선택해서 +1 해서 반환

---

int countOneChildNodes(BTNode *node)
자식 노드가 1개인 노드의 개수 출력하기
예시)

-> 출력 결과 2

int countOneChildNodes(BTNode *node) {

	if (node == NULL) {
    	return 0;
    }
    //왼쪽 자식만 있는 경우
    if (node-> left != NULL && node->right == NULL) {
    	return countOneChildNodes(node->left) +1;
    }
    //오른쪽 자식만 있는 경우
    else if (node-> right != NULL && node->left == NULL) {
    	return countOneChildNodes(node->right) +1 ;
    } 
    //양쪽 자식 모두 있는 경우
    else {
    	return countOneChlidNodes(node->left) + countOneChildNodes(node->right); 
    }

}

---

int sumOfOddNodes (BTNode *node)
: 홀수 노드들의 합을 구하는 함수

int sumOfOddNodes(BTNode *node) {
	if (node == NULL) {
    	return 0; 
    }
    
    
    int cnt = 0;
    //노드의 item 값이 홀수라면 더한다. 
    if (node->item %2 != 0) {
    	cnt += node-> item;
    }
    
    cnt += sumOfOddNodes(node->left);
    cnt += sumOfOddNodes(node->right);
    
    return cnt; 
	


}

---

void mirrorTree(BTNode *node)

중위 순회를 이용하여 출력
중위 순회(inorder traversal): 왼쪽 자식 -> 루트 -> 오른쪽 자식
위의 예시의 출력값: 1 2 3 4 6 5

void mirrorTree(BTNode *node) {
	if (node == NULL) {
    	return 0;
    }
    
    BTNode *temp;
    
    //왼쪽 서브트리
	//오른쪽 서브트리 -> 미러 이미지 생성
    mirrorTree(node->left);
    mirrorTree(node->right);
    
    temp = node->left;
    node->left = node->right;
    node->right = temp;

}

---

void printSmallerValues(BTNode *node, int m)
: m 보다 작은 값들 출력하기
전위 순회 방식으로 출력
전위 순회: 루트 -> 왼쪽 자식 -> 오른쪽 자식

void printSmallerValues(BTNode *node, int m) {
	if (node == NULL) {
    	return 0;
    }
    
    if (node->item < m) {
    	printf("%d ", node-> item);
    }
	
    printSmallerValues(node->left, m);
    printSmallerValues(node->right,m); 

}

node의 item이 m 보다 작으면 출력
-> 전위 순회이기 때문에 재귀적으로
node->left, node-> right 순서로 탐색

---

smallestValue(BTNode *node)
최솟값 return 하는 함수

-> 10을 return 하도록

int smallestValue(BTNode *node) {
	
    if (node == NULL) {
    	return __INT_MAX__;
    }	
    
    int minValue;
    minValue = node->item;
    
    int leftMinValue = smallestValue(node->left);
    int rightMinValue = smallestValue(node->right);
    
    if (leftMinValue < minValue && leftMinValue < rightMinValue) {
    	return leftMinValue;
    } 
    else if (rightMinValue < minValue && rightMinValue < leftMinValue) {
    	return rightMinValue;
    }
    
    return minValue;


}

if (node == NULL) -> 빈 트리, 노드가 없는 상황
최솟값을 찾을 수 없으므로 정수의 최댓값을 return 한다.

현재 노드의 값, 왼쪽 서브트리의 최솟값, 오른쪽 서브트리의 최솟값을 비교해서 가장 작은 값을 return

---

int hasGreatGrandchild(BTNode *node)
증손자 노드를 갖는 노드의 값을 출력한다.

great Grand child 20, 15를 가지는 50을 return 해야 한다.

위에서 만든 maxHeight(BTNode *node) 활용

int hasGreatGrandchild(BTNode *node) {
	if (node == NULL) {
    	return 0;
   	}
    
    int depth;
    depth = maxHeight(node);
    
    if (depth >=3) {
    	printf("%d ", node-> item);
    }
}

증손자 노드를 가지려면 depth가 최소 3이상이어야 하니까 이를 활용한다.