백준 2162 선분그룹(CCW와 선분교차판정)

CCW(counter-clockwise)

2차원 공간에서 세 점으로 구성된 두 벡터의 회전 방향을 계산하는 기법.
볼록 껍질을 찾기 위한 그레이엄 스캔, 선분 교차 판정 등에 쓰인다.
두 (2차원)벡터의 cross product의 값이 반시계 방향일 때 양수, 시계 방향일 때 음수가 나오는 성질을 이용한다.

예시: (1, 0)×(0, 1)=1, (0, 1)×(1, 0)=-1
네?

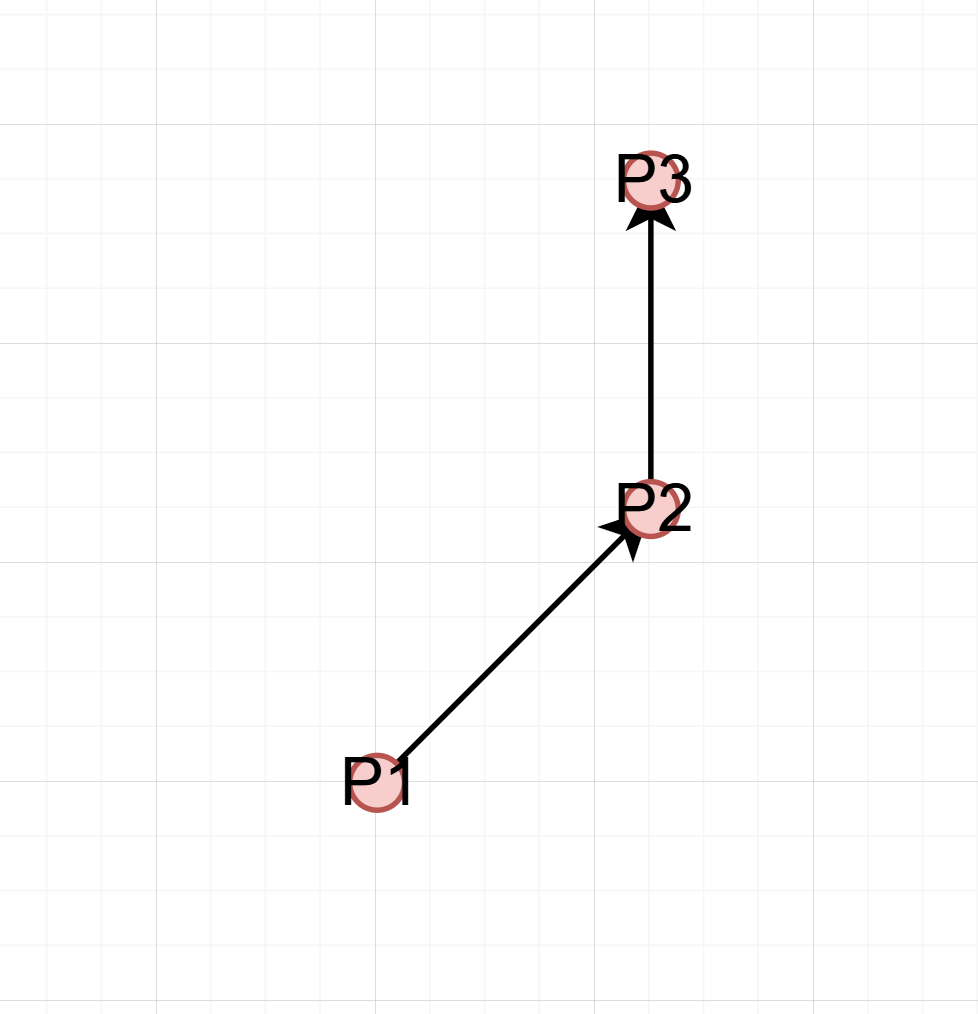
$P1 = (x1, y1),\; P2 = (x2, y2),\; P3 = (x3, y3)$일 때 P1을 원점으로 정규화하고
$V1 = (x2-x1, y2-y1),\; V2 = (x3-x1, y3-y1)$ 두 벡터의 cross product 값을 구하면
$V1×V2 = (x2-x1)(y3-y1)-(x3-x1)(y2-y1)$이며 이 값이 양수이면 반시계, 음수이면 시계, 0이면 평행한 방향이다.
따라서 CCW는
$CCW=sign((x2-x1)(y3-y1)-(x3-x1)(y2-y1))$로 쓸 수 있다(sign은 선택적)

def ccw(p0, p1, p2):
    x0, y0 = p0
    x1, y1 = p1
    x2, y2 = p2

    return (x1-x0)*(y2-y0) - (x2-x0)*(y1-y0)

선분 교차 판정

두 선분이 교차하는지를 검사하는 방법.
선분의 기울기와 x, y의 범위로 판정하는 방법과 ccw를 이용하는 방법 등이 있다.
ccw를 이용하는 방법이 조금 더 간단하므로 이 방법을 소개한다.

선분이 접하는 경우에는 교차하지 않는다고 볼 수도 있으나 밑에서 풀 백준 문제에서는 접하는 경우에도 같은 그룹으로 판정하므로 그러한 경우까지 살펴본다.

케이스를 세 가지로 나눠서 살펴보면
case 1. P3, P4가 P1, P2를 지나는 직선으로 만들어지는 이분면의 같은 쪽에 속해있는 경우

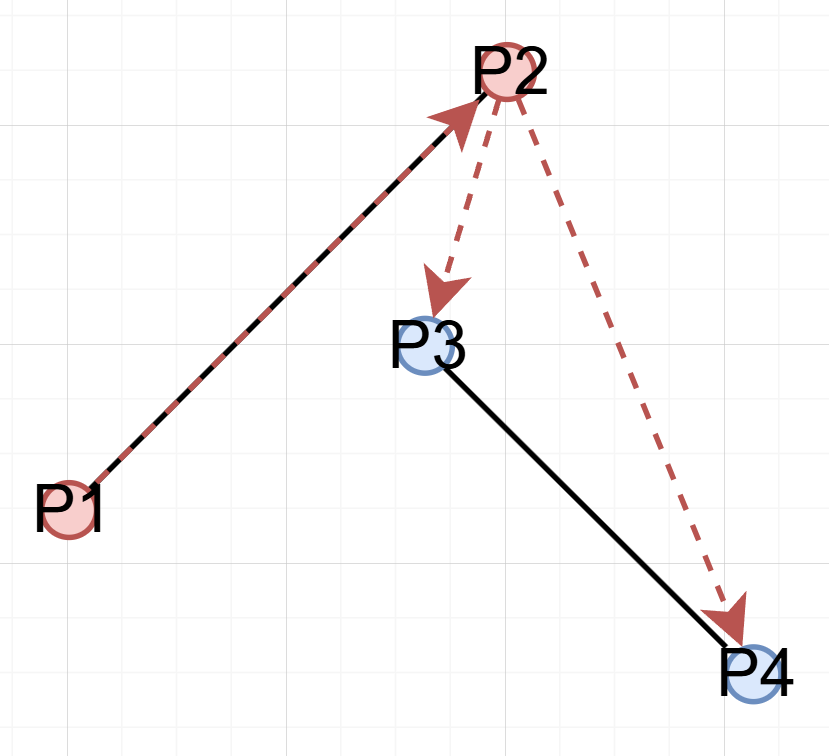
$CCW(P1, P2, P3)*CCW(P1, P2, P4) > 0$이다.
무슨 짓을 해도 두 선분이 교차할 수 없다.

case 2. P3, P4가 P1, P2를 지나는 직선으로 만들어지는 각기 다른 이분면에 속해있는 경우

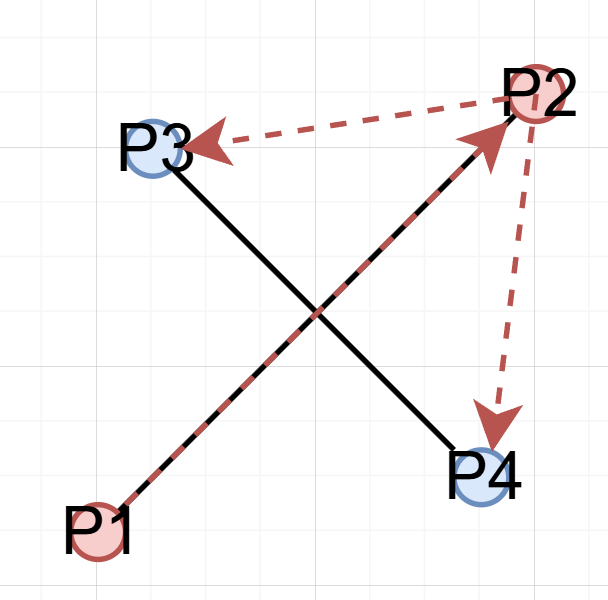
이 경우 P1, P2가 이루는 벡터와 P2, P3가 이루는 벡터의 ccw($CCW(P1, P2, P3)$)는 양수이고 $CCW(P1, P2, P4)$는 음수이다.
즉 $CCW(P1, P2, P3)*CCW(P1, P2, P4) < 0$

case 2-1. 교차하는 경우

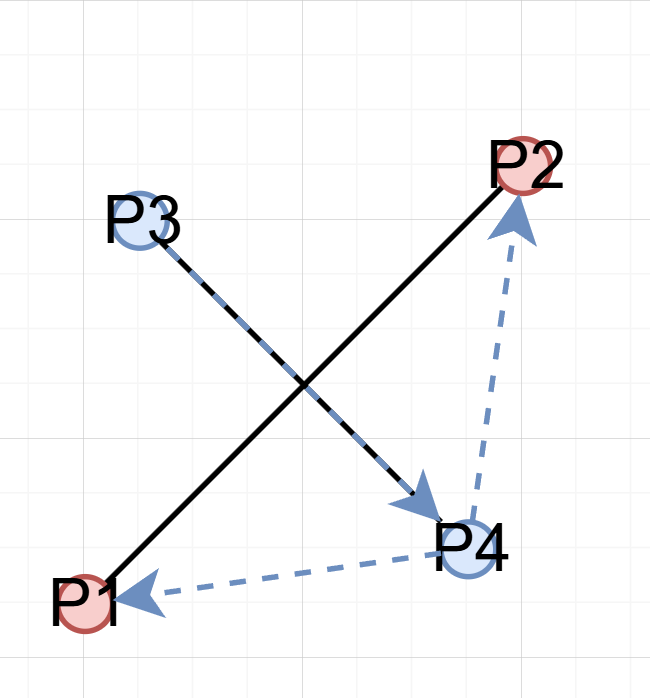
$CCW(P3, P4, P1)*CCW(P3, P4, P2) < 0$이다.

case 2-2. 교차하지 않는 경우

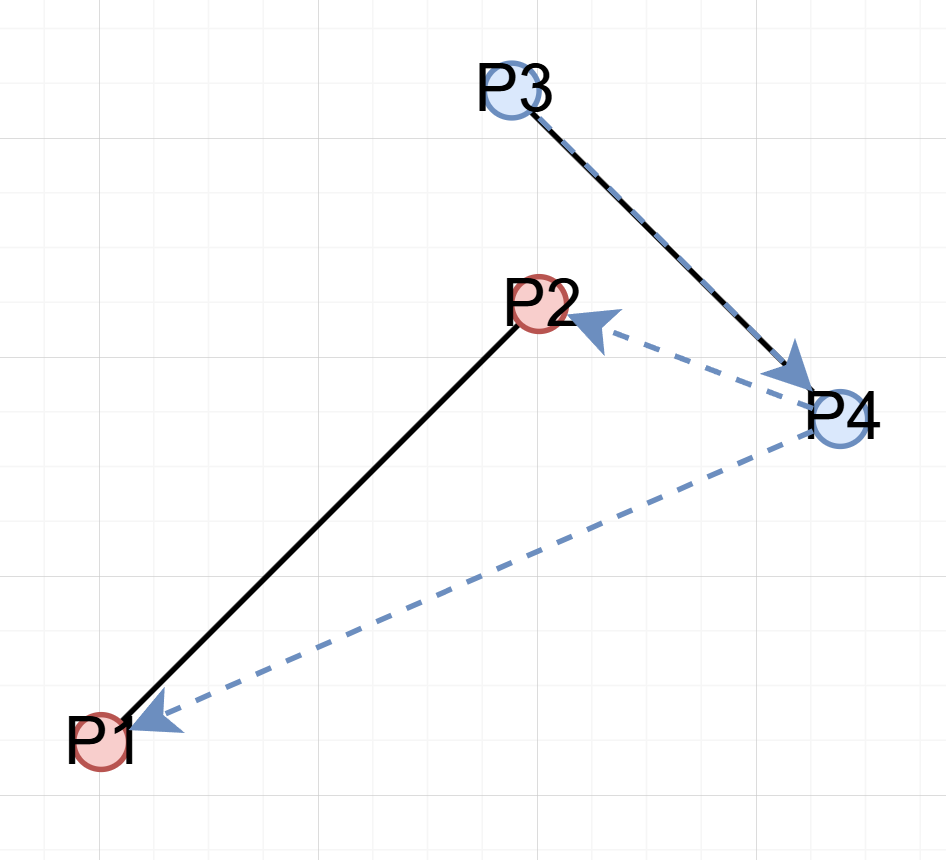
$CCW(P3, P4, P1)*CCW(P3, P4, P2) > 0$이다.

case 2-3. 접하는 경우

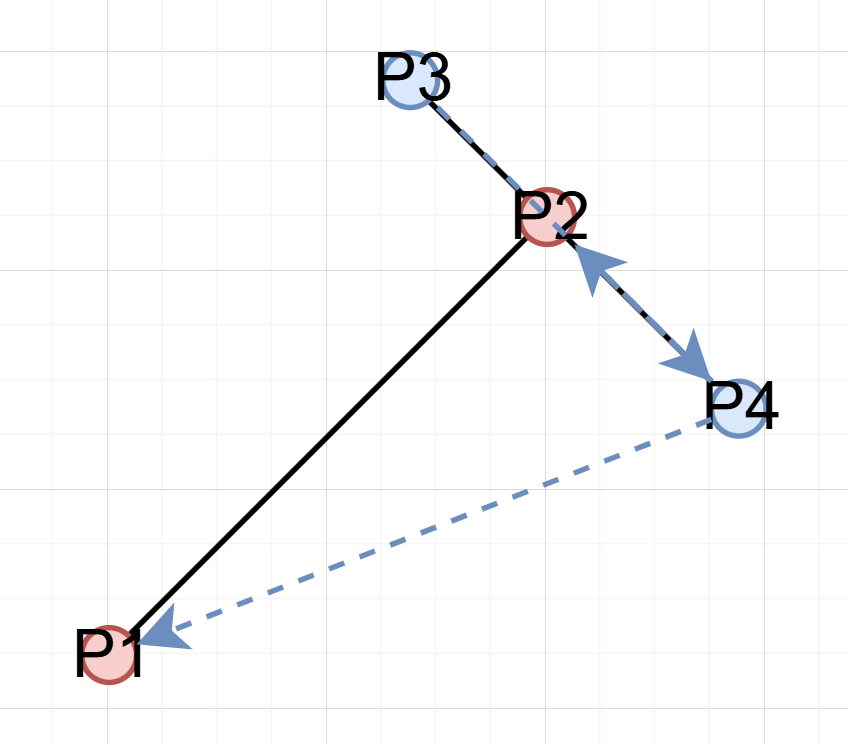
P1에 접하는 경우 $CCW(P3, P4, P1) = 0$,
P2에 접하는 경우 $CCW(P3, P4, P2) = 0$이다.
즉 $CCW(P3, P4, P1)*CCW(P3, P4, P2) = 0$이다.

case 3. P3, P4 중 하나 이상이 P1, P2를 지나는 직선 위에 있는 경우

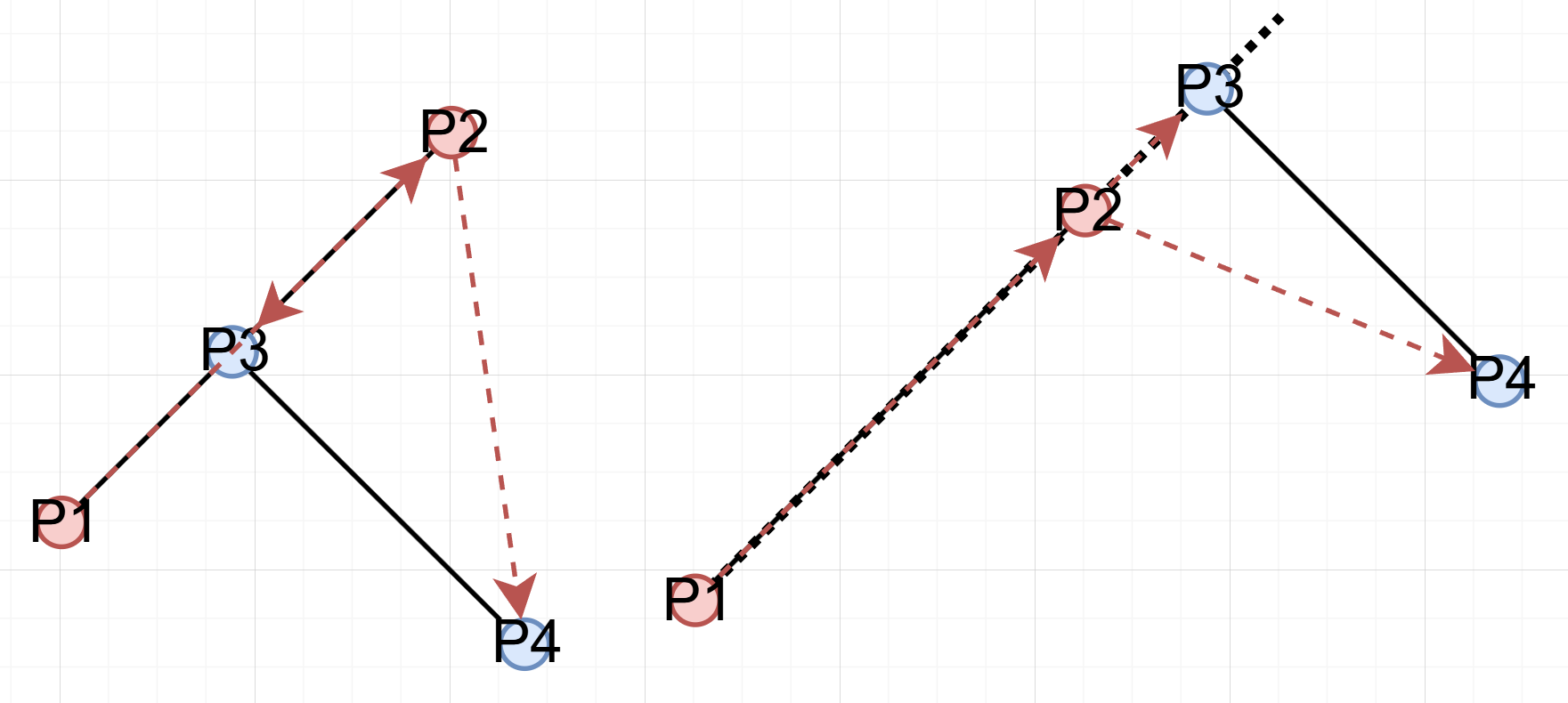
$CCW(P1, P2, P3)*CCW(P1, P2, P4) = 0$이다.

case 3-1. 하나만 직선 위에 있는 경우

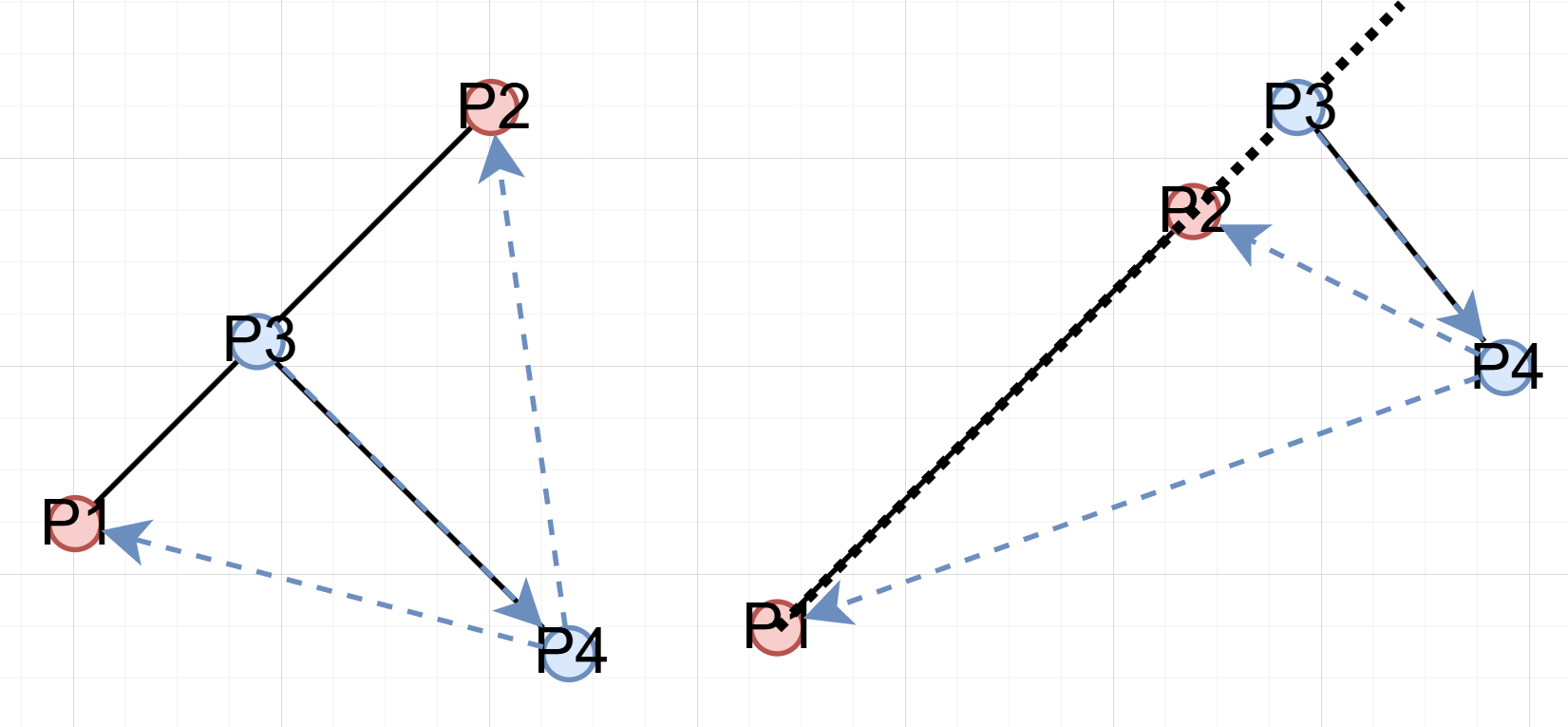
P3가 P1, P2 직선 위에 있을 때를 가정하면
$CCW(P3, P4, P1)*CCW(P3, P4, P2) < 0$이면 접한다.
$CCW(P3, P4, P1)*CCW(P3, P4, P2) > 0$이면 접하지 않는다.

case 3-2. 둘 다 직선 위에 있는 경우(같은 직선에 있는 두 선분)

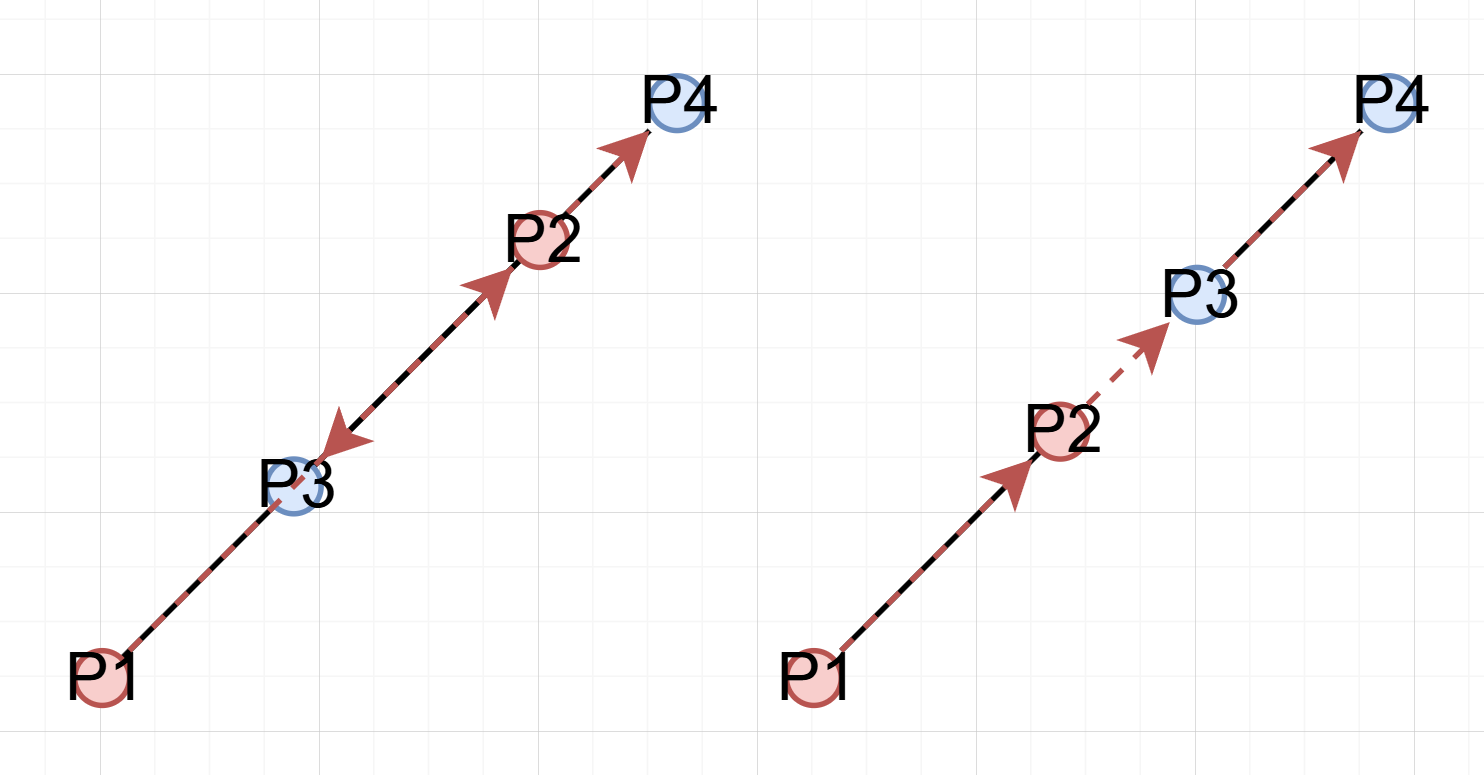
$CCW(P1, P2, P3)=CCW(P1, P2, P4)=CCW(P3, P4, P1)=CCW(P3, P4, P2)=0$이다.
이 경우 접하는지 여부는 P3, P4 중 하나 이상이 선분 P1P2위에 있는지를 살펴봐야 한다.

def dot_on_line(dot, line):
    x0, y0, x1, y1 = line
    x, y = dot

    return min(x0, x1) <= x <= max(x0, x1) and min(y0, y1) <= y <= max(y0, y1)

이상의 내용을 표로 정리하면 아래와 같다.

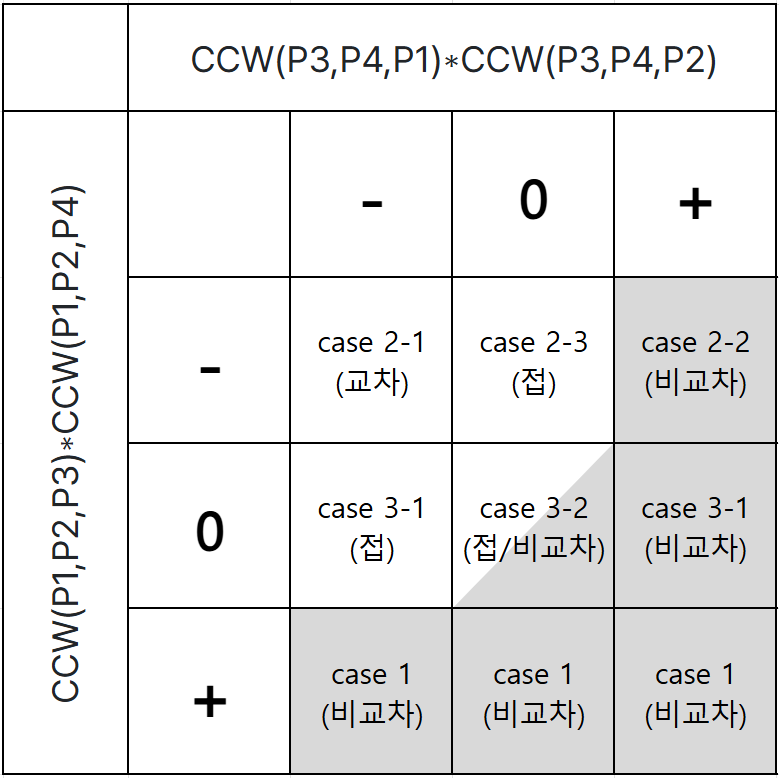
def intersection(l1, l2):
    x1, y1, x2, y2 = l1
    x3, y3, x4, y4 = l2
    
    v1, v2, v3, v4 = (x1, y1), (x2, y2), (x3, y3), (x4, y4)

    ccw1 = ccw(v1, v2, v3)
    ccw2 = ccw(v1, v2, v4)
    ccw3 = ccw(v3, v4, v1)
    ccw4 = ccw(v3, v4, v2)

	# case2 or case 3 판정
    if (ccw12:=ccw1 * ccw2) <= 0 and (ccw34:=ccw3 * ccw4) <= 0:
    	# case 2-1, 2-3, 3-1 판정
        if ccw12 < 0 or ccw34 < 0:
            return True
        
        # case 3-2의 접하는지 여부 판정
        if dot_on_line(v3, v1+v2):
            return True
        if dot_on_line(v4, v1+v2):
            return True
        if dot_on_line(v1, v3+v4):
            return True
        if dot_on_line(v2, v3+v4):
            return True
        
    return False

2162 선분그룹

문제

두 선분이 만나는 경우(교차하거나 접하는 경우)에 두 선분은 서로 같은 그룹에 있다.
선분들이 주어졌을 때 몇 개의 그룹이 존재하고 가장 많은 선분을 포함한 그룹의 선분 수를 찾아야 한다.

풀이

선분을 하나씩 추가해가며 이미 추가한 선분들과 그룹을 이루는 선분이 있는지를 찾는다.
이미 그룹을 이룬 선분과 만나는 경우 그룹을 결합한다.

중복 검사를 최대한 피하기 위해 선분의 x축 기준 왼쪽 경계(min(x1, x2))를 기준으로 정렬 후, 오른쪽 경계(max(x1, x2))가 새로 추가할 선분의 왼쪽 경계보다 왼쪽에 있는 경우에는 교차판정을 건너 뛰도록 했다.

N = int(input())
lines = []
for i in range(N):
    x1, y1, x2, y2 = map(int, input().split())
    lines.append((x1, y1, x2, y2) if x1 <= x2 else (x2, y2, x1, y1))

lines.sort(key=lambda x: (x[0], x[2]))

parents = [i for i in range(N)]
for i in range(N):
    for j in range(i):
    	# (N-1)(N-2)/2 번 반복된다.
        if lines[j][2] < lines[i][0]:
        	# 아래 continue문이 최대한 많이 호출되기 위해서는 lines가 x1, x2를 기준으로 정렬되어야 한다.
            continue
        if intersection(lines[i], lines[j]):
            p_i = find_parent(i)
            p_j = find_parent(j)
            parents[max(p_i, p_j)] = min(p_i, p_j)

groups = defaultdict(int)
for i in range(N):
    groups[find_parent(i)] += 1
    
print(len(groups))
print(max(groups.values()))