오늘 배운 것들

1. 그래프와 트리

1-1. 그래프

정점과 간선으로 이루어진 자료구조.
위 조건만 만족한다면 뭐든 그래프라고 할 수 있다.
단방향, 양방향, 가중치, 연결, 자기순환 등
네트워크를 모델링할 때나 연결구조를 가진 모든 상황을 모델링할 때 쓰인다.

1-1-1. 인접행렬을 이용한 표현

그래프의 연결관계를 행렬을 이용하여 표현한 것.
정점이 $n$개일 때 $n×n$행렬 $A$를 인접행렬이라고 할 때 $A_{i j}$는 정점 $i$에서 정점 $j$로의 비용이다.(갈 수 없는 경우는 보통 0)
무방향 그래프라면 대칭행렬일 것이다.

1-1-2. 인접리스트를 이용한 표현

트리를 구현할 때와 같이 각 노드들을 연결리스트를 이용하여 표현한 것.
노드는 연결되어 있는 인접 노드들을 가리키는 포인터를 가지고 있다.
간선이 적은 경우에 직관적으로 표현할 수 있다.

1-2. 트리

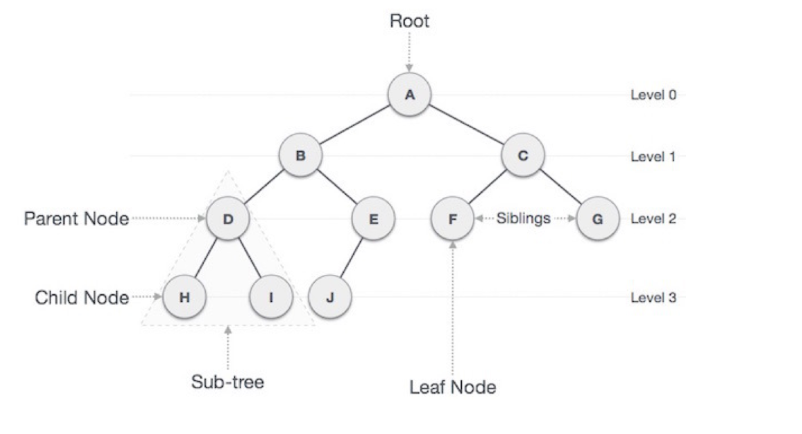순환(자기순환 포함)이 없는 그래프이다.
따라서 두 노드 사이의 경로는 유일해진다.
하나 더 추가한다면 루트노드가 있어야 한다.

1-2-1. 이진트리

자식 노드가 2개 이하인 트리.
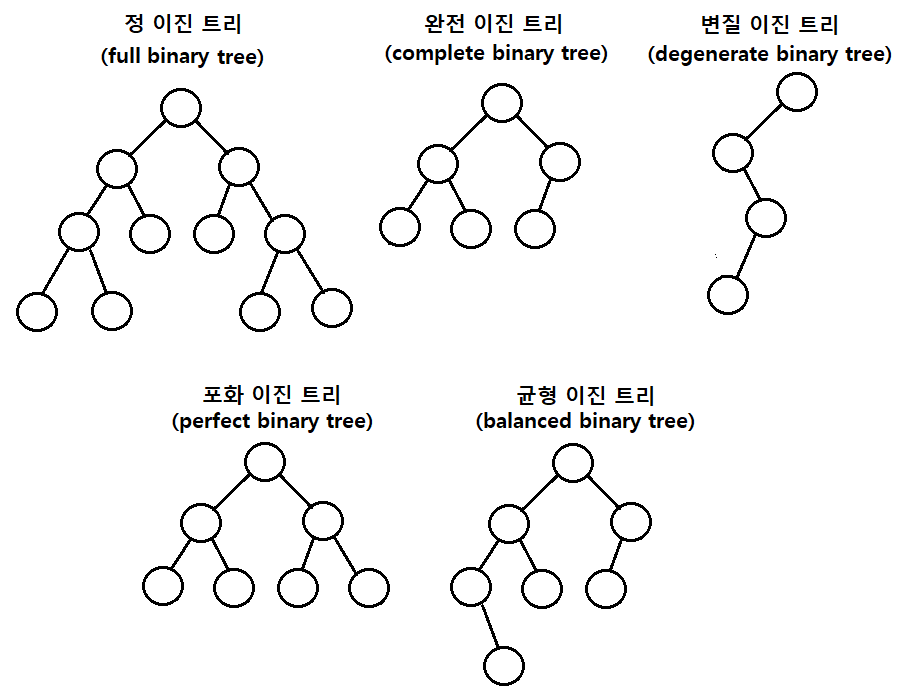종류도 여러가지다.

• 이진트리의 순회
  이진트리의 순회 방법은 전위/중위/후위 순회가 있다.
  루트노드를 먼저/중간에/마지막에 하는지에 따라 나뉜다.
  자식트리는 무조건 왼쪽이 먼저다.

  전위순회: 루트노드 - 왼쪽트리 - 오른쪽트리
  중위순회: 왼쪽트리 - 루트노드 - 오른쪽트리
  후위순회: 왼쪽트리 - 오른쪽트리 - 루트노드

구현도 재귀적으로 하고 직접 세어볼 때에도 재귀적으로 하면 편하다.

1-2-2. 이진탐색트리

탐색을 위한 트리.
루트노드보다 작은 노드는 왼쪽에 큰 노드는 오른쪽에 위치한다.
모든 서브트리에 대해서도 위 조건을 만족하는 트리가 이진탐색트리이다.
값 탐색 시 트리의 높이가 log2가 되도록 잘 분배(비선형적)되어 있다면 $O(log(n))$에 탐색할 수 있지만, 선형트리 등 그렇지 않은 경우에는 n번의 탐색이 필요하다.($O(n)$)

1-2-3. AVL트리

이진탐색트리와 같은 성질을 갖는다.
다만 모든 자식노드에 대하여 왼쪽 오른쪽 서브트리의 높이 차이가 1이하로 유지되도록 삽입/삭제가 일어난다.
따라서 최악의 경우에도 $O(log(n))$의 탐색 시간복잡도를 유지한다.
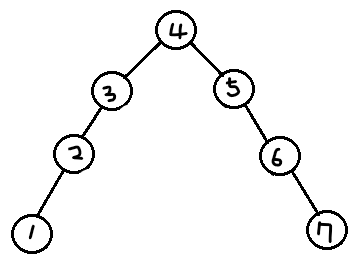처음에는 같은 레벨의 서브트리끼리 비교하는 줄 알고 위 사진같은 경우도 AVL 트리 아닌가 생각했다.(3과 5, 2와 6, 1과 7의 높이가 같으므로..)
실제로는 왼쪽 오른쪽 자식끼리 비교해야 하기 때문에 AVL 트리가 아니다.
3의 왼쪽은 높이 2, 오른쪽은 높이 0이므로 높이차이가 2이다.

1-2-4. B트리

기본적으로 트리 구조를 가지나 각 노드마다 여러 개(일반적으로 2-3개)의 데이터와 자식 노드를 가질 수 있다.
데이터를 탐색하는 방식은 이진탐색트리와 유사하다.
각 노드의 데이터들 사이에는 해당하는 자식 노드를 가리키는 인덱스를 가지고 있는데
어떤 노드가 9와 15라는 데이터를 가지고 있다면 9앞에는 9보다 작은, 9와 15사이에는 9보다 크고 15보다 작은, 15뒤에는 15보다 큰 데이터를 가진 서브노드를 가리키는 인덱스를 가지고 있다.

1-2-5. 트라이(trie)

문자열을 탐색할 때 사용하는 자료구조로 대소비교를 통해 탐색하지 않고 문자를 선택하며 트리를 탐색한다.
문자열을 빠르게 탐색할 수 있지만 모든 문자들을 다 담아야 하므로 문자열이 많다면 메모리를 매우 많이 사용한다.

1-3. 신장 트리(Spanning Tree)

그래프의 부분 그래프. 근데 이제 간선의 수가 최소인
$n$개의 정점을 모두 연결하기 위해서는 최소 $n-1$개의 간선이 필요하다.
따라서 순환이 없으므로 트리의 정의를 만족한다.
네트워크를 최소한의 간선으로 연결하려고 한다면 신장 트리를 구하면 된다.

1-3-1. 최소 신장 트리(MST)

신장 트리 중에서도 간선의 가중치 합이 최소가 되는 신장 트리
신장 트리의 조건까지 고려하면 최소 신장 트리는

1. 순환이 없어야 함(트리)
2. $n-1$개의 간선만을 사용할 것(신장 트리)
3. 그중 간선의 가중치가 최소가 되는 경우(최소 신장 트리)

의 조건을 만족해야 한다.

1-3-2. 크루스칼 알고리즘

간선 선택 알고리즘
가중치가 적은 순서부터 사이클이 형성되지 않도록 $n-1$개의 간선들을 차례대로 선택한다.
사이클 형성을 효율적으로 판단하는 것이 중요하다.
간선이 적을 때 유리하다.

• 왜 최소 신장트리를 보장하는가?
  역순으로 간선이 모두 존재하는 상태에서 간선을 지워간다고 생각한다면,

1-3-3. 프림 알고리즘

정점 선택 알고리즘
임의의 정점에서 시작해 최소 간선으로 연결된 정점을 선택해가며 트리를 확장한다.
(현재 트리와 인접한 가장 작은 가중치를 가진 간선을 선택하므로 매 번 가장 최적의 선택이 된다.)
이미 선택한 정점은 다시 선택하지 않으므로 사이클 형성을 별도로 파악하지 않아도 된다.
정점이 적을 때 유리하다.

2. 문제풀이

2-1. 이진 검색 트리(백준 5639)

from __future__ import annotations
import sys

sys.setrecursionlimit(100000)

class Node:
    def __init__(self, key: any, value: any=None, left: Node=None, right: Node=None) -> None:
        self.key = key
        self.value = value
        self.left = left
        self.right = right
    def __repr__(self) -> str:
        return self.value if self.value else self.key

class BinarySearchTree:
    def __init__(self, root: Node | None=None) -> None:
        self.root = self.current = root
    
    def preorder(self, root: Node) -> list:
        result = []
        result += [root.key]
        if root.left:
            result += self.preorder(root.left)
        if root.right:
            result += self.preorder(root.right)
        return result
    
    def inorder(self, root: Node) -> list:
        result = []
        if root.left:
            result += self.inorder(root.left)
        result += [root.key]
        if root.right:
            result += self.inorder(root.right)
        return result
    
    def postorder(self, root: Node) -> list:
        result = []
        if root.left:
            result += self.postorder(root.left)
        if root.right:
            result += self.postorder(root.right)
        result += [root.key]
        return result

    def search(self, key: any) -> Node:
        current = self.root
        while current is not None:
            if current.key > key:
                if current.left is not None:
                    current = current.left
                else:
                    break
            elif current.key < key:
                if current.right is not None:
                    current = current.right
                else:
                    break
            else:
                break
        return current
    
    def insert(self, node: Node) -> None:
        next = self.search(node.key)
        if next is None:
            self.root = node
        elif next.key < node.key:
            next.right = node
        elif next.key > node.key:
            next.left = node
    
def main() -> None:
    N = [int(i) for i in sys.stdin]
    N.reverse()
    
    tree = BinarySearchTree()
    while N:
        tree.insert(Node(N.pop()))
    print("\n".join(map(str, tree.postorder(tree.root))))
        
    
main()

이진 검색 트리를 구현하는 문제.

2-2. 최소 스패닝 트리(백준 1197)

import sys

def make_edge(x: str | int, 
              y: str | int, 
              weight: str | int) -> tuple[int, tuple[int]]:
    return (int(weight), (min(int(x), int(y)), max(int(x), int(y))))

def main() -> None:
    def find_parent(i: int) -> int:
        while parents[i] != i:
            i = parents[i]
        return i
    
    V, E = [int(i) for i in sys.stdin.readline().split()]
    EDGES = sorted([make_edge(*sys.stdin.readline().split()) for _ in range(E)], key=lambda x: x[0], reverse=True)

    parents = {i: i for i in range(1, V+1)}
    min_weight = 0
    count = 1
    while count < V:
        weight, e = EDGES.pop()
        if (p0:=find_parent(e[0])) != (p1:=find_parent(e[1])):
            count += 1
            min_weight += weight
            parents[p1] = p0
            parents[e[0]] = p0
        elif e[0] == e[1] and weight < 0:
            min_weight += weight

    print(min_weight)

main()

사이클이 형성되는지 파악하기 위해서 부모 노드를 value로 갖는 딕셔너리를 사용하였다.
find_parent함수가 반복문을 사용하므로 반복문이 많이 실행되지 않도록 부모를 갱신할 경우 형제 노드의 부모 값도 매번 변경해주어야 한다.

3. 잡다한 배움

• 파이썬 위키에 자료형의 메소드 별 시간복잡도를 정리해 놓은 페이지
  https://wiki.python.org/moin/TimeComplexity

• 스택을 스레드마다 독립적으로 가지는 이유
  스택은 함수 호출 시 전달되는 인자, 작업 후 되돌아갈 주소값 및 함수 내에서 선언하는 변수 등을 저장하기 위해 사용되는 메모리 공간이다.
  이에 스택 메모리 공간이 독립적이라는 것은 독립적인 함수 호출이 가능하다는 것이고 이는 독립적인 실행 흐름이 추가되는 것이다.
  따라서 스레드의 정의에 따라 독립적인 실행 흐름을 추가하기 위한 최소 조건으로 독립된 스택을 할당한다.

• PC 레지스터를 스레드마다 독립적으로 가지는 이유
  PC값은 스레드가 명령어의 어디까지 수행하였는지를 나타내게 된다.
  스레드는 CPU를 할당받았다가 스케쥴러에 의해 다시 선점당한다. 그렇기 때문에 명령어가 연속적으로 수행되지 못하고 어느 부분까지 수행했는지 기억할 필요가 있다. 따라서 PC 레지스터를 독립적으로 할당한다