MUSIC 알고리즘을 이용한 AoA 추정

jswboseok·2023년 1월 3일
신호및시스템신호처리
0

MUSIC (Multiple Signal Classification)

MIMO (Multi Input Multi Output) 환경에서 여러 개의 안테나에서 발생하는 phase 차이를 이용하여 모델링한 신호를 분해하고 적절한 알고리즘을 통해 Angle of Arrival (혹은 Direction of Arrival)을 구하는 것이 목적이다.

Signal Modeling

다음 그림은 Multi-Antenna에서 얻을 수 있는 신호의 모습을 나타낸다.

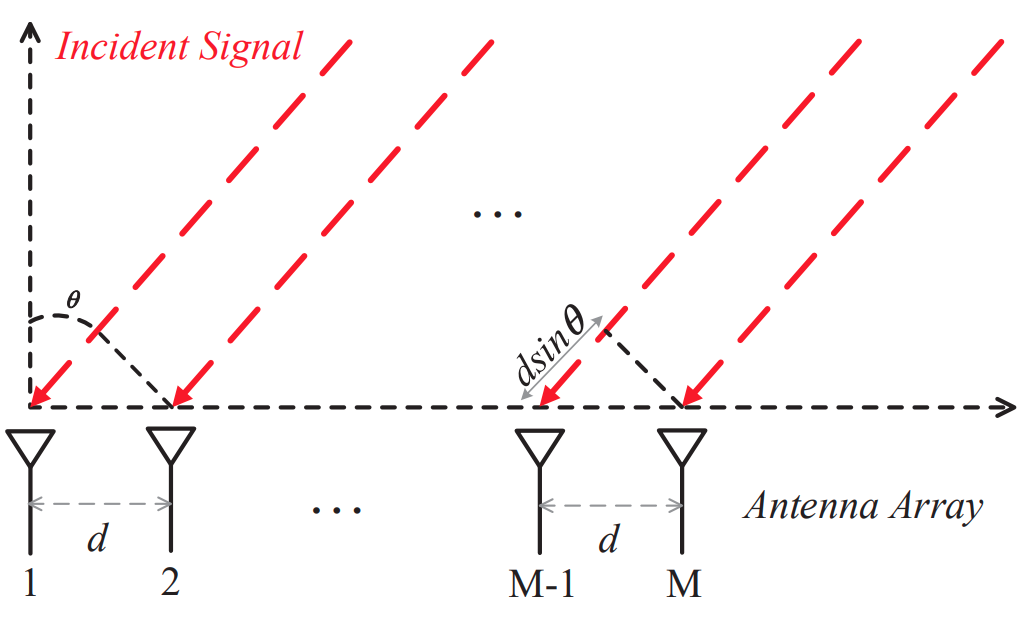
(그림 출처 : AFall: Wi-Fi-based Device-free Fall Detection System using Spatial Angle of Arrival [1] )

이 때 phase difference φ\varphi는 다음과 같이 나타낼 수 있다.

φ(θ)=e−j2πfdsinθc\varphi(\theta)=e^{-j2{\pi}f{dsin\theta\over{c}}}

θ\theta는 AoA, ff는 중심 주파수, dd는 안테나 사이의 거리, cc는 빛의 속도이다.
이를 통해 antenna array의 phase difference를 벡터로 나타내면 다음과 같다. 다른 말로 steering vector 라고도 한다.

a(θ)=[1,φ(θ),φ(θ)2,...,φ(θ)(M−1)]T\boldsymbol{a}(\theta)=[1, \varphi(\theta),\varphi(\theta)^2, ... ,\varphi(\theta)^{(M-1)}]^{\mathsf{T}}

이 때, ii 번째 안테나에서 수신된 신호는 다음과 같이 나타낼 수 있다.

xi(t)=φ(θ)(i−1)s(t)+ni(t)x_i(t) = \varphi(\theta)^{(i-1)}s(t)+n_i(t)

여기서 s(t)s(t)는 첫 번째 안테나에서 수신된 신호를 나타내고 ni(t)n_i(t)는 ii 번째 안테나에서 받은 noise를 의미한다.

또한 전체 안테나에서 수신된 신호를 벡터로 다음과 같이 나타낼 수 있다.

X(t)=[x1(t),x2(t),...,xM(t)]T=a(θ)s(t)+N(t)\boldsymbol{X}(t)=[x_1(t), x_2(t), ...,x_M(t)]^{\mathsf{T}} = \boldsymbol{a}(\theta)s(t)+\boldsymbol{N}(t)

Multipath 환경을 고려한다면, 수신되는 신호는 multipath 개수만큼 존재할 것이다. Multipath 환경에서 LL 개의 multi signal이 존재한다면,

X(t)=∑l=1La(θl)sl(t)+N(t)=AS(t)+N(t)\boldsymbol{X}(t)= \sum_{l=1}^L\boldsymbol{a}(\theta_l)s_l(t)+\boldsymbol{N}(t)=\boldsymbol{A}\boldsymbol{S}(t)+\boldsymbol{N}(t)

여기서 L<ML<M이다. 즉 안테나 개수가 multipath의 개수보다 많아야 한다.

EVD of the Signal and get Noise Vector

위 신호는 단순히 수식적으로 모델링만 한 것이지, 우리가 실제로 안테나로부터 알 수 있는 값 자체는 X(t)\boldsymbol{X}(t)이다.

우선 X(t)\boldsymbol{X}(t)의 autocorrelation을 구하면 다음과 같다.

RXX=E[XXH]=E[(AS+N)(AS+N)]=AE[SSH]AH+E[NNH]=ARSAH+RN\begin{aligned} &\boldsymbol{R}_{\boldsymbol{X}\boldsymbol{X}}=E[\boldsymbol{X}\boldsymbol{X}^H]\\ &=E[(\boldsymbol{A}\boldsymbol{S}+\boldsymbol{N})(\boldsymbol{A}\boldsymbol{S}+\boldsymbol{N})]\\ &=\boldsymbol{A}E[\boldsymbol{S}\boldsymbol{S}^H]\boldsymbol{A}^H+E[\boldsymbol{N}\boldsymbol{N}^H]\\ &=\boldsymbol{A}\boldsymbol{R_S}\boldsymbol{A}^H+\boldsymbol{R}_{\boldsymbol{N}} \end{aligned}

다만 실제로 저렇게 RXX\boldsymbol{R}_{\boldsymbol{X}\boldsymbol{X}}를 구하는 것은 어렵기 때문에 현실적인 application에서는 X\boldsymbol{X}의 sample을 KK개 모아서 평균을 내는 방식으로 근사값을 구하게 된다.

R^X=1K∑k=1KXXH{\boldsymbol{\hat{R}}_{\boldsymbol{X}}}={1\over{K}}\sum_{k=1}^K\boldsymbol{X}\boldsymbol{X}^H

어쨋든 이렇게 R^X\boldsymbol{\hat{R}}_\boldsymbol{X}를 구했으면 이 autocorrelation 값에 eigen value decomposition을 적용할 수 있게 된다. 즉

R^Xvi=λivi\boldsymbol{\hat{R}}_\boldsymbol{X}v_i=\lambda_iv_i

가 되며, R^X\boldsymbol{\hat{R}_X}가 MM차원의 벡터이기 때문에 결과적으로 총 MM 개의 eigenvalue와 eigenvector를 얻게 된다. 여기서 MM은 안테나의 개수이다. 이때 R^X\boldsymbol{\hat{R}_X}는 Hermitian이기 때문에 각 eigenvector들 끼리는 orthogonal하다.

eigenvalue를 크기에 대해 내림차순으로 정렬하면, 정렬된 eigenvalue Λ=[λ1,λ2,...,λM]\Lambda=[\lambda_1,\lambda_2,...,\lambda_M]와 그에 대응하는 eigenvector V=[v1,v2,...,vM]V=[v_1, v_2, ..., v_M]를 얻게 된다.

Noise floor[2]에 의하면 noise 차원은 상대적으로 작은 eigenvalue를 갖게 된다. 따라서 위 eigenvector V=[v1,v2,...,vM]V=[v_1, v_2, ..., v_M]를 signal과 관련된 eigenvector VS=[v1,v2,...,vL]V_{S}=[v_1, v_2, ..., v_L]와 noise와 관련된 eigenvectorVN=[vL+1,vL+2,...,vM]V_{N}=[v_{L+1}, v_{L+2}, ..., v_M]로 나눌 수 있다.

위에서 RXX=ARSAH+RN\boldsymbol{R}_{\boldsymbol{X}\boldsymbol{X}}=\boldsymbol{A}\boldsymbol{R_S}\boldsymbol{A}^H+\boldsymbol{R}_{\boldsymbol{N}}에서 직관적으로 알 수 있듯이 MM차원의 RXX\boldsymbol{R}_{\boldsymbol{X}\boldsymbol{X}}는 LL차원의 RS\boldsymbol{R_S}와 나머지 RN\boldsymbol{R_N}으로 이루어진 것을 알 수 있다. 따라서 RXX\boldsymbol{R}_{\boldsymbol{X}\boldsymbol{X}}는 MM개의 eigenvector를 갖고 그 중 LL개의 eigenvector는 RS\boldsymbol{R_S}의 eigenvector이고 나머지 M−LM-L개는 RN\boldsymbol{R_N}의 eigenvector가 된다.

AoA Estimation

PMUSICP_{MUSIC} 함수를 다음과 같이 정의한다.

PMUSIC(θ)=1aH(θ)VNVNHa(θ)P_{MUSIC}(\theta)={1\over{\boldsymbol{a}^H(\theta)V_N{V_N}^H}\boldsymbol{a}(\theta)}

PMUSICP_{MUSIC} 을 최대로 만드는 것은 a(θ)\boldsymbol{a}(\theta)와 VNV_N이 orthogonal한 지점이다. 다만 현실에서는 항상 Noise가 존재하기 때문에 a(θ)\boldsymbol{a}(\theta)와 VNV_N이 정확히 orthogonal하지는 못하다.

따라서 PMUSICP_{MUSIC} 을 최대로 만드는 θ\theta의 값을 찾는다. (The sharpest peak of PMUSIC(θ)P_{MUSIC}(\theta))

θ^=arg max⁡θ PMUSIC(θ)\hat{\theta}=\underset{\theta}{\argmax}\ P_{MUSIC}(\theta)

일반적으로 AoA는 −π2≤θ≤π2-{\pi\over{2}} \le\theta\le{\pi\over{2}}범위에서 가지므로 −π2-{\pi\over{2}}에서 π2{\pi\over{2}}까지 1도 혹은 0.5도 (사용자 마음)씩 변화시켜가며 PMUSIC(θ)P_{MUSIC}(\theta)를 최대로 만드는 θ\theta를 찾는다.

모든 각도에 대해서 계산하면 더 정확한 AoA를 얻을 수 있지만 계산량이 늘어나므로 일반적으로 1도나 0.5도씩 비교한다

결과적으로 θ^\hat{\theta}가 우리가 원하는 AoA의 값이 된다.

Appendix

MUSIC 알고리즘을 본격적으로 진행하기 전에, MUSIC 알고리즘에서 사용되는 간단한 선형대수학 지식들을 짚고 넘어가겠다.

Hermitian Matrix

  • 정의 : A complex squared matrix that is equal to it's own conjugate transpose

  • A=AT‾, ai,j=aj,i‾A=\overline{A^{\mathsf{T}}},\ a_{i,j}=\overline{a_{j,i}}

  • ex)

    (22+i42−i3i4−i1)\begin{pmatrix} 2 & 2+i & 4 \\ 2-i & 3 & i \\ 4 & -i & 1\end{pmatrix}

  • Hermitian 끼리 더하고 product 곱을 해도 그 결과는 Hermitian이다.

Hermitian Conjugate

  • 행렬을 transpose시킨 후 conjugate 시킨다. 기호로 여러개가 있는 것 같은데, 본 포스팅에서는 HH로 나타내겠다.

  • ex)

    A=(1−2−i1+ii), AH=(11−i−2+ii)A=\begin{pmatrix} 1 & -2-i \\ 1+i & i \end{pmatrix},\ A^H=\begin{pmatrix} 1 & 1-i \\ -2+i & i \end{pmatrix}

  • AA가 Hermitian 행렬이면, AHA^H도 Hermitian 행렬이다.

  • 임의의 행렬 AA에 대하여 AAHAA^H와 AHAA^HA도 Hermitian 행렬이다.

Reference

[1] S. Chen, W. Yang, Y. Xu, Y. Geng, B. Xin and L. Huang, "AFall: Wi-Fi-based Device-free Fall Detection System using Spatial Angle of Arrival," in IEEE Transactions on Mobile Computing, Early Access, 2022
[2] https://en.wikipedia.org/wiki/Noise_floor
[3] https://www.diva-portal.org/smash/get/diva2:724272/FULLTEXT01.pdf

profile
jswboseok
냠냠
이전 포스트

12/19일 알고리즘 스터디

다음 포스트

1/16일 알고리즘 스터디 (1)

0개의 댓글