링크텍스트
위 강의를 듣고 정리하는 글입니다.
discrete RV
5.1 Bernoulli and Binomial random variables
Bernoulli RV
X ∼ B e r n o u l l i ( p ) X \sim Bernoulli(p) X ∼ B e r n o u l l i ( p ) ∼ \sim ∼
pmf
P ( X = 0 ) = 1 − p P(X=0) = 1-p P ( X = 0 ) = 1 − p P ( X = 1 ) = p P(X=1) = p P ( X = 1 ) = p
→ 앞면이 나올 확률이 p p p
Binomial RV
Y ∼ B i n o m i a l ( n , p ) Y \sim Binomial(n,p) Y ∼ B i n o m i a l ( n , p ) → 위 동전을 n n n
pmf
P ( Y = i ) = ( n i ) p i ( 1 − p ) n − i P(Y=i) = \binom{n}{i}p^i(1-p)^{n-i} P ( Y = i ) = ( i n ) p i ( 1 − p ) n − i i = 0 , 1 , . . . , n i = 0, 1, ..., n i = 0 , 1 , . . . , n
( n i ) \binom{n}{i} ( i n )
Y = X 1 + X 2 + . . . + X n Y = X_1 + X_2 + ... + X_n Y = X 1 + X 2 + . . . + X n E [ X i ] = 0 ∗ ( 1 − p ) + 1 ∗ p = p E[X_i] = 0*(1-p) + 1*p = p E [ X i ] = 0 ∗ ( 1 − p ) + 1 ∗ p = p V a r [ Y ] = n p ( 1 − p ) Var[Y] = np(1-p) V a r [ Y ] = n p ( 1 − p )
5.2 Poisson RV
n p = c o n s t a n t λ np =constant\ λ n p = c o n s t a n t λ
P o s s i o n ( λ ) = lim n − > inf Y Possion(λ) = \lim_{n->\inf}Y P o s s i o n ( λ ) = n − > i n f lim Y 예시) 어떤 매장에 1시간동안 들어오는 고객의 수(지나가는 사람은 많고(매우 큰 n) 그 사람들 중 들어올 확률 p는 적을 때)
pmf
P ( X = i ) = e − λ λ i i ! P(X=i) = e^{-λ}\frac{λ^i}{i!} P ( X = i ) = e − λ i ! λ i i = 0 , 1 , 2 , 3 , … i=0, 1, 2, 3, … i = 0 , 1 , 2 , 3 , …
∑ i = 0 inf P ( i ) = ∑ i = 0 inf e − λ λ i i ! = e − λ ∑ i = 0 inf λ i i ! = e − λ e λ = 1 \sum^{\inf}_{i=0}P(i) = \sum^{\inf}_{i=0}e^{-λ}\frac{λ^i}{i!} = e^{-λ}\sum^{\inf}_{i=0}\frac{λ^i}{i!} = e^{-λ}e^{λ} = 1 i = 0 ∑ i n f P ( i ) = i = 0 ∑ i n f e − λ i ! λ i = e − λ i = 0 ∑ i n f i ! λ i = e − λ e λ = 1 ∑ i = 0 inf λ i i ! = e λ \sum^{\inf}_{i=0}\frac{λ^i}{i!} = e^{λ} ∑ i = 0 i n f i ! λ i = e λ
mgf
Φ ( t ) = E [ e t x ] = ∑ i = 0 inf e t i P ( i ) = e λ ( e t − 1 ) Φ(t)=E[e^{tx}] = \sum_{i=0}^{\inf}e^{ti}P(i) = e^{λ(e^t-1)} Φ ( t ) = E [ e t x ] = ∑ i = 0 i n f e t i P ( i ) = e λ ( e t − 1 ) Φ ’ ( 0 ) = λ = E [ X ] Φ’(0) = λ = E[X] Φ ’ ( 0 ) = λ = E [ X ]
geometric RV
X ∼ g e o m e t r i c ( p ) X \sim geometric(p) X ∼ g e o m e t r i c ( p )
동전을 던질 때 첫 앞면 나올 때까지 i 번 던질 확률
pmf
P ( X = i ) = ( 1 − p ) i − 1 p P(X=i) = (1-p)^{i-1}p P ( X = i ) = ( 1 − p ) i − 1 p E [ X ] = 1 p E[X]=\frac{1}{p} E [ X ] = p 1
conditional expectation technique
E [ X ] = E [ E [ X ∣ Y ] ] E[X] = E[E[X|Y]] E [ X ] = E [ E [ X ∣ Y ] ]
Y = 0 Y=0 Y = 0
Y = 1 Y=1 Y = 1
X X X
E [ X ] = ( 1 − p ) E [ X ∣ Y = 0 ] + p E [ X ∣ Y = 1 ] E[X] = (1-p)E[X|Y=0] + pE[X|Y=1] E [ X ] = ( 1 − p ) E [ X ∣ Y = 0 ] + p E [ X ∣ Y = 1 ]
= ( 1 − p ) ( E [ X ] + 1 ) + p ( 1 ) = (1-p)(E[X]+1) + p(1) = ( 1 − p ) ( E [ X ] + 1 ) + p ( 1 )
E [ X ∣ Y = 0 ] = E [ X ] + 1 E[X|Y=0]=E[X]+1 E [ X ∣ Y = 0 ] = E [ X ] + 1 E [ X ] E[X] E [ X ] E [ X ∣ Y = 0 ] E[X|Y=0] E [ X ∣ Y = 0 ]
continuous RV
X ∼ U n i f o r m ( α , β ) X \sim Uniform(\alpha, \beta) X ∼ U n i f o r m ( α , β )
pdf
f ( x ) = 1 β − α i f α ≤ x ≤ β f(x) = \frac{1}{\beta - \alpha} \ \ if \ \ \alpha ≤ x ≤ \beta f ( x ) = β − α 1 i f α ≤ x ≤ β f ( x ) = 0 o t h e r w i s e f(x) = 0 \ \ otherwise f ( x ) = 0 o t h e r w i s e
5.5 Normal(Gaussian) RV
X ∼ N o r m a l ( μ , σ 2 ) X \sim Normal(\mu, \sigma^2) X ∼ N o r m a l ( μ , σ 2 ) f ( x ) = 1 2 π σ 2 e − ( x − μ ) 2 ) 2 σ 2 f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-(x-\mu)^2)}{2\sigma^2}} f ( x ) = 2 π σ 2 1 e 2 σ 2 − ( x − μ ) 2 )
5.6 Exponential RV
X ∼ E x p o n e n t i a l ( λ ) X \sim Exponential(\lambda) X ∼ E x p o n e n t i a l ( λ )
pdf
f ( x ) = λ e − λ x ( x ≥ 0 ) f(x) = \lambda e^{-\lambda x} \ \ \ \ \ \ (x ≥ 0) f ( x ) = λ e − λ x ( x ≥ 0 ) f ( x ) = 0 ( x < 0 ) f(x) = 0 \ \ \ \ \ \ (x < 0) f ( x ) = 0 ( x < 0 )
Memoryless
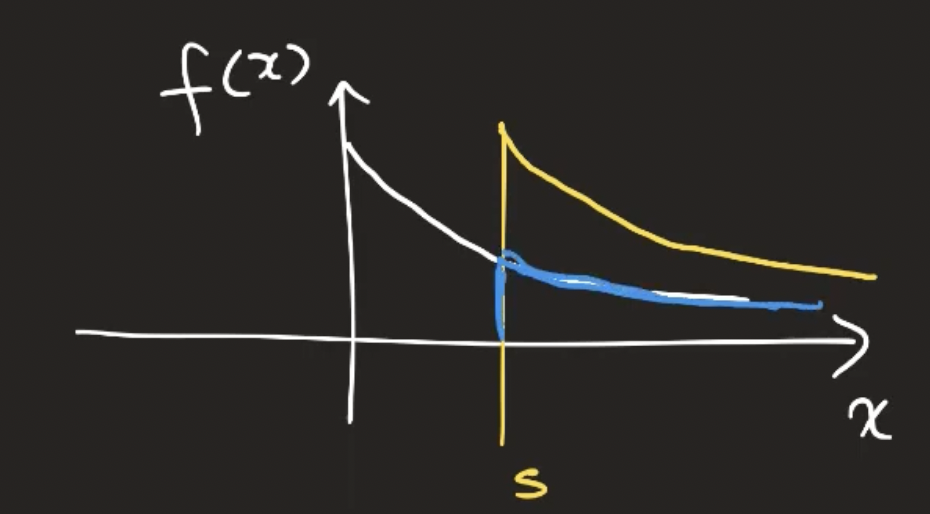
P ( X > s + t ∣ X > t ) = P ( X > s ) P(X>s+t|X>t) = P(X>s) P ( X > s + t ∣ X > t ) = P ( X > s ) 예를 들어 X X X s = 5 s = 5 s = 5 t = 3 t=3 t = 3
좌변: 형광등을 3일 쓰고 이 형광등을 최소 5일 더 쓸 확률
우변: 새 형광등을 5일 넘게 쓸 확률
→ 좌변은 중고 아니니? → 형광등의 수명이 Exponential RV로 모델링 될 때는 형광등을 썼다는 memory가 없음(새거랑 헌거랑 구분이 안됨) → 아래 그림이 exponential RV의 pdf인데 s일만큼 썼다고 pdf가 파란색으로 바뀌면 안됨(파란색 그래프는 면적이 1이 아니기 때문에 s일 썼더라도 노란색 그래프(원래 pdf와 동일)가 되어야겠지)
random variable X X X
random variable이 n개 모이면 random vector [ X 1 , X 2 , … , X n ] [X_1, X_2, …, X_n] [ X 1 , X 2 , … , X n ]
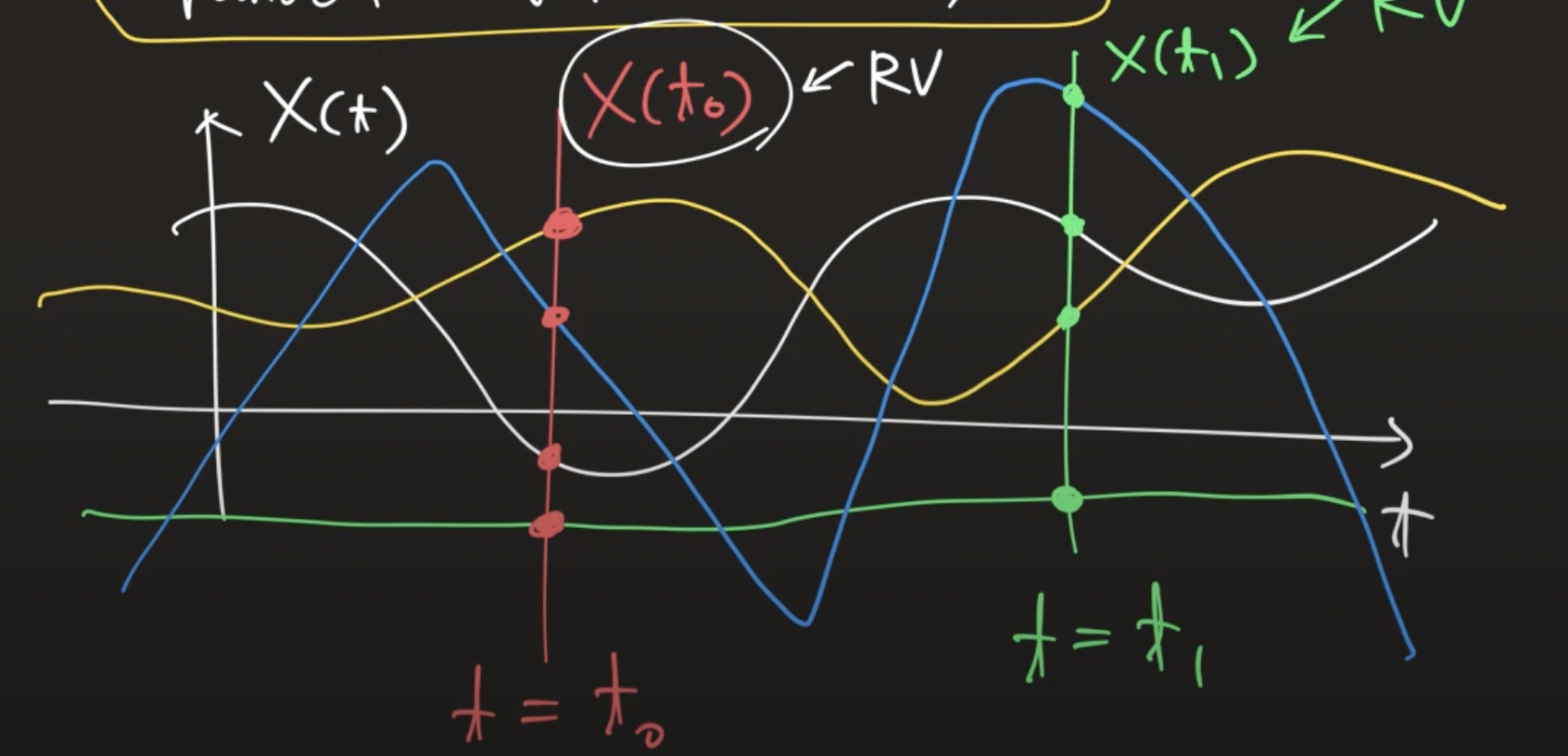
random variable이 무한개면 random process X ( t ) X(t) X ( t )
random process: 시간에 따른 RV(시간에 따른 확률적인 변화를 가지는 구조)
5.7 gamma distribution
X ∼ g a m m a ( α , λ ) α > 0 , λ > 0 X \sim gamma(\alpha, \lambda) \ \ \ \ \ \ \alpha > 0, \ \lambda > 0 X ∼ g a m m a ( α , λ ) α > 0 , λ > 0 f ( x ) = λ e − λ x ( λ x ) α − 1 Γ ( α ) ( x > = 0 ) f(x) = \frac{\lambda e^{-\lambda x}(\lambda x)^{\alpha -1}}{Γ(\alpha)} \ \ \ \ \ (x>=0) f ( x ) = Γ ( α ) λ e − λ x ( λ x ) α − 1 ( x > = 0 ) f ( x ) = 0 ( x < 0 ) f(x)=0 \ \ \ \ \ \ (x<0) f ( x ) = 0 ( x < 0 )
gamma function
Γ ( α ) = ∫ 0 inf e − y y α − 1 d y Γ(\alpha) = \int^{\inf}_0e^{-y}y^{\alpha - 1}dy Γ ( α ) = ∫ 0 i n f e − y y α − 1 d y Γ ( α ) = ( α − 1 ) Γ ( α − 1 ) Γ(\alpha)=(\alpha - 1)Γ(\alpha - 1) Γ ( α ) = ( α − 1 ) Γ ( α − 1 ) Γ ( 1 ) = 1 Γ(1) = 1 Γ ( 1 ) = 1 Γ ( n ) = ( n − 1 ) ! Γ(n) = (n-1)! Γ ( n ) = ( n − 1 ) !
5.8 Distributions arising from the normal
normal distribution으로부터 파생된 distribution
5.8.1 The chi-square distribution
Z i ∼ N ( 0 , 1 ) Z_i \sim N(0, 1) Z i ∼ N ( 0 , 1 )
Z 1 , Z 2 , . . . , Z n : i i d R V s Z_1, Z_2, ..., Z_n: iid \ RVs Z 1 , Z 2 , . . . , Z n : i i d R V s
X = Z 1 2 + … + Z n 2 X = Z_1^2 + … + Z_n^2 X = Z 1 2 + … + Z n 2
relation between chi-square and gamma RVs
χ n 2 = g a m m a ( n 2 , 1 2 ) χ_n^2 = gamma(\frac{n}{2}, \frac{1}{2}) χ n 2 = g a m m a ( 2 n , 2 1 ) 위 식 n n n 2 2 2
χ n 2 = g a m m a ( 1 , 1 2 ) = e x p ( 1 2 ) χ_n^2 = gamma(1, \frac{1}{2}) = exp(\frac{1}{2}) χ n 2 = g a m m a ( 1 , 2 1 ) = e x p ( 2 1 ) 5.8.2 t-distribution
T n = Z χ n 2 n T_n = \frac{Z}{\sqrt{\frac{χ_n^2}{n}}} T n = n χ n 2 Z