⌚시간복잡도

• 알고리즘 문제를 해결할 때 단순히 문제에 대한 답을 찾기만 하면 알고리즘의 효율성이 떨어질 수 있다.
• 알고리즘의 효율성은 시간복잡도라는 개념을 통해 살펴볼 수 있다.

시간복잡도 : 알고리즘의 성능을 설명하는 것으로 알고리즘이 실행되는 동안 수행하는 기본적인 연산의 수를 입력의 크기에 대한 함수로 표현

• 시간 복잡도는 Big-O(빅오) 표기법으로 표현할 수 있다.
• 빅오 표기법은 O(...)로 표기하며, 이때 괄호 안에는 어떤 함수가 들어간다. O(n), o(logn) 등으로 표현할 수 있으며, O를 읽을 때는 Order로 읽을 수 있다.
• 일반적으로 변수 n으로 입력의 크기를 나타낸다.

⚡ 자주 접할 수 있는 시간 복잡도

⭐ O($1$)

상수 시간 알고리즘으로 입력의 크기에 영향을 받지 않는 일정한 수행 속도를 가지고 있다. 반복문을 활용하지 않고 출력값을 얻어낼 수 있다.

//정삼각형의 한변의 길이를 입력받고 삼각형의 높이를 구하는 프로그램
#include<bits/stdc++.h>
using namespace std;
int main(){
    int n;
    cin>>n;
    cout<<sqrt(3)/2*n;
}

⭐ O($n$)

선형 시간 알고리즘으로 입력에 비례하여 처리시간이 선형적으로 증가한다. 대부분의 경우에 가장 효율적인 시간 복잡도이며, 답을 구하기 위해서 입력값을 순차적으로 한번 살펴보고 결과를 얻을 수 있는 경우이다.

//n개의 정수를 입력받고 특정값을 찾는 알고리즘
//찾으려는 값이 입력값의 가장 마지막에 있을 때 최악의 상황에 O(n)이 소요된다. 
#include<bits/stdc++.h>
using namespace std;
int main(){
    int n;
    cin>>n;
    vector<int> v(n);
    for(int i=0;i<n;i++){
        cin>>v[i];
    }
    int find;
    cin>>find;
    for(int i=0;i<n;i++){
        if(v[i]==find){
            cout<<"found";
            break;
        }
    }
}

⭐ O($logn$)

로그 시간 알고리즘으로 대체로 단계마다 입력의 크기를 절반씩 줄여 나간다. 입력 N이 커질 때 수행횟수가 logN에 비례해서 증가하는 경우 O(n)보다 수행 속도가 좋다.

• O(logn)으로 수행되는 대표적인 알고리즘은 이진탐색이다. 이진탐색은 내가 찾고자 하는 값이 정렬된 배열의 중간 값보다 크면 중간값을 포함한 하위 값들은 탐색 대상에서 제외된다. 반대로 찾고자 하는 값이 배열의 중간 값보다 작으면 중간 값을 포함한 상위 값들은 탐색에서 제외된다.
• 즉 단계마다 탐색의 범위를 절반씩 줄여나간다. 따라서 이분탐색의 알고리즘의 수행 시간은 로그 시간이다.
  
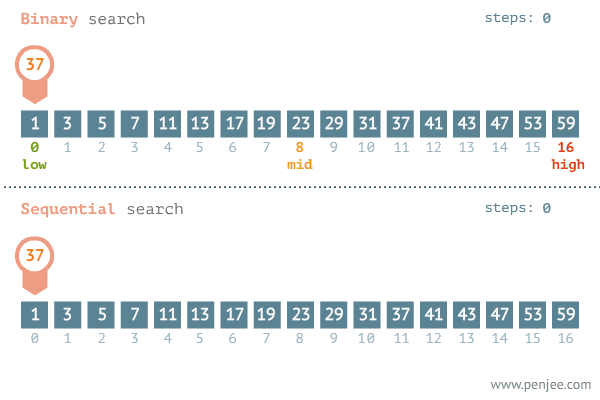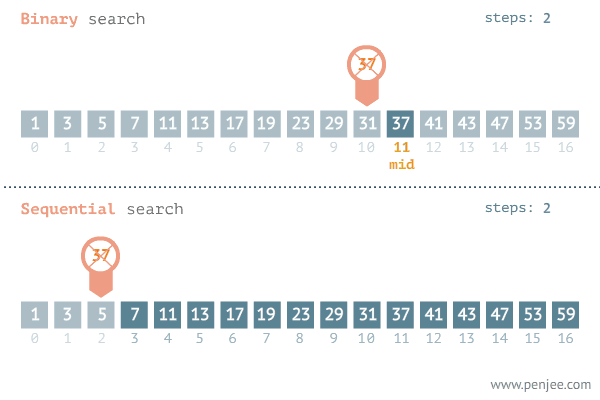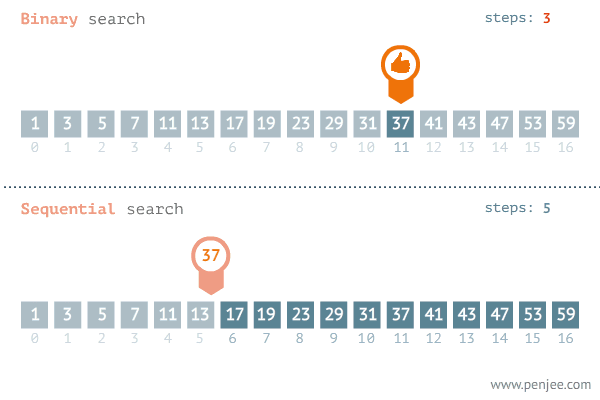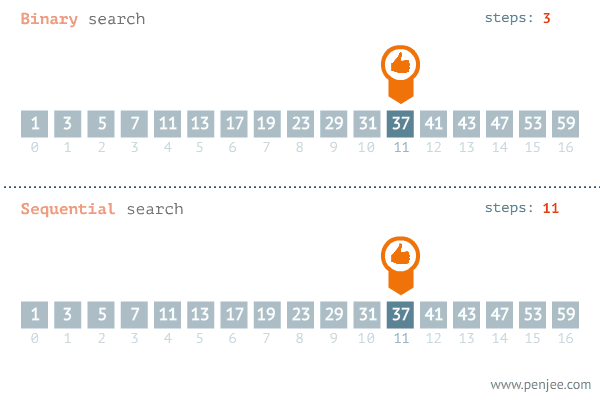
  출처 : https://blog.penjee.com/binary-vs-linear-search-animated-gifs/

⭐ O($n^2$)

제곱 시간 알고리즘은 보통 2중으로 중첩된 반복문을 사용할 경우 발생하는 시간 복잡도이다. 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가한다.

for(int i=0;i<n;i++){
   for(int j=0;j<n;j++){
   //do something
   }
}

• 다음은 가장 대표적인 $O(n^2)$ 시간복잡도를 가지고 있는 버블정렬 알고리즘이다.

void bubble_sort(int list[], int n){
  int i, j, temp;

  for(i=n-1; i>0; i--){
    // 0 ~ (i-1)까지 반복
    for(j=0; j<i; j++){
      // j번째와 j+1번째의 요소가 크기 순이 아니면 교환
      if(list[j]<list[j+1]){
        temp = list[j];
        list[j] = list[j+1];
        list[j+1] = temp;
      }
    }
  }
}

⭐ O($nlogn$)

연산을 한번 수행할 때마다 $O(logn)$의 수행시간을 사용하는 알고리즘
주로 입력을 효율적으로 정렬하는 알고리즘이 가지고 있는 시간 복잡도이다.

• 대표적인 알고리즘으로 힙정렬, 머지정렬 알고리즘이 있다.

⭐ O($2^n$)

입력 크기가 커질 때 연산수가 $2^n$에 비례해서 증가하는 시간복잡도이다.
대표적인 알고리즘으로 피보나치의 수를 구하는 알고리즘이다.

int func (int n) {
  if (n <= 1) 
    return n;
  return func(n-1) + fun(n-2);
}

• 한번 함수를 호출할 때마다 두번씩 재귀로 함수를 호출하기 때문에 $O(2^n)$시간복잡도를 가지고 있다.

성능비교

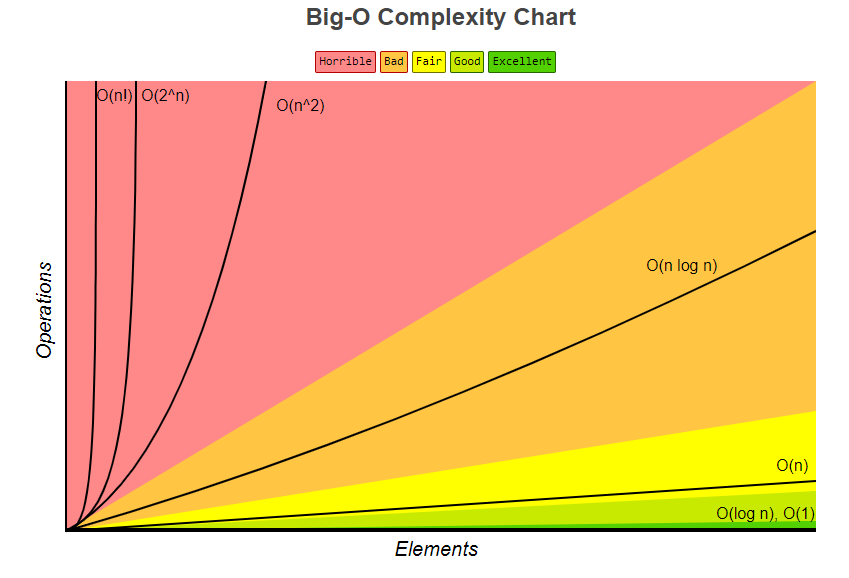출처 : https://www.bigocheatsheet.com/

O($1$) > O($logn$) > O($n$) > O($nlogn$) > O($n^2$) > O($2^n$)