최대공약수와 최소공배수

최대공약수(Greatest Common) Divisor

• 공약수(common divisor)란 두 수 이상의 여러 수의 공통된 약수
• 최대공약수(GCD)란 두 수 이상의 여러 수의 공약수 중 최대인 수

최소공배수(Lowest Common Multiple)

• 공배수(common multiple)란 두 수 이상의 여러 수의 공통된 배수
• 최소공배수(LCM)란 두 수 이상의 여러 수의 공배수 중 최소인 수

두 수를 소인수 분해를 한 뒤, 두 수의 공통된 소인수를 모두 곱하면, 최대공약수, 두 수의 모든 소인수를 곱하면 최소공배수

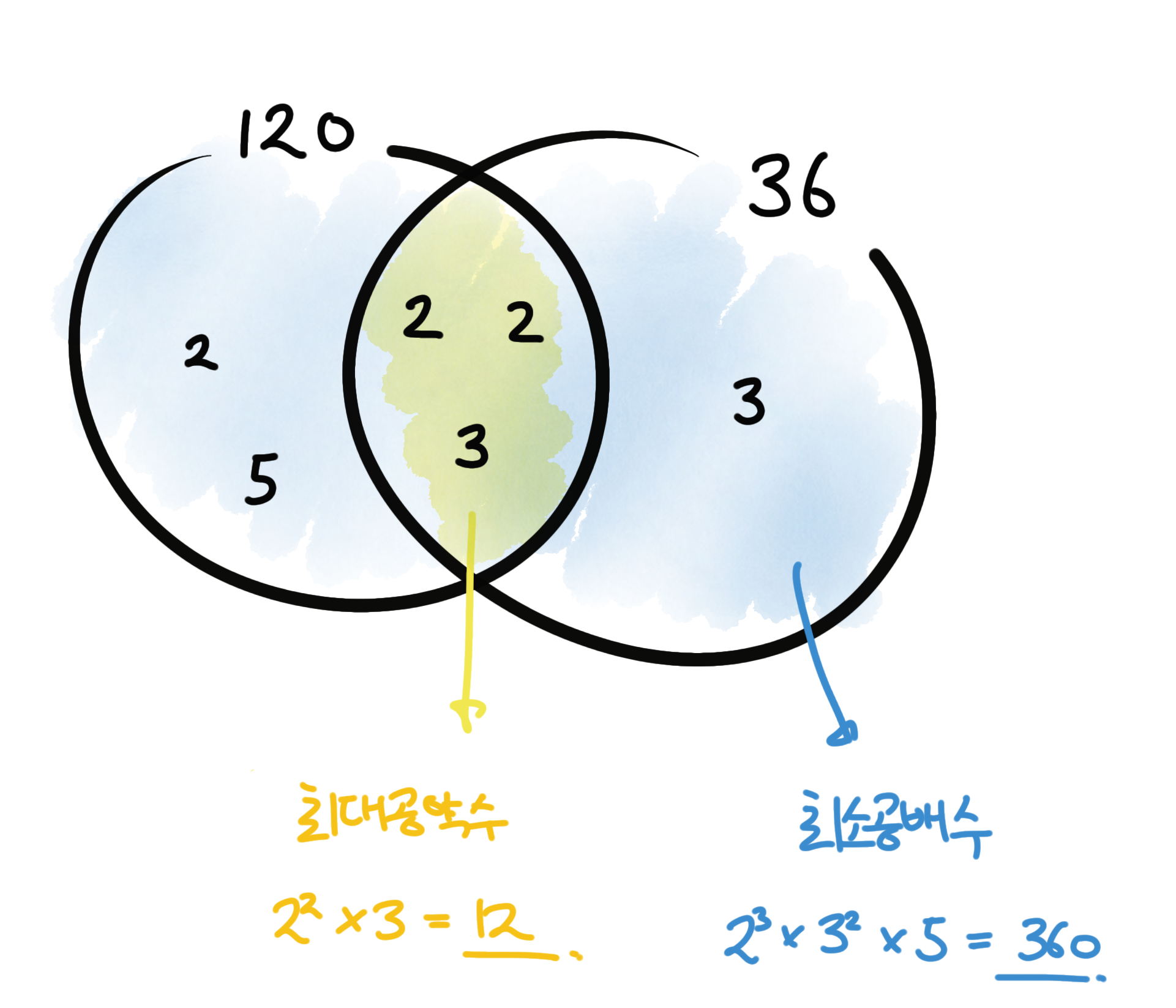출처 : https://dimenchoi.tistory.com/46

위 그림을 참고하여 정리하면 두수 A,B의 최대공약수를 G, 최소공배수를 L이라고 하면, 다음 식이 성립된다.

AB=LG

유클리드 호제법

정의 : 유클리드 호제법

유클리드 호제법은 다음에 기인한다.

A를 B로 나눈 몫을 Q라 하고, 나머지를 R이라 하자. 이 때, gcd(A,B) = gcd(B,R)이다.

예시를 보면 1071과 1029의 나머지는 42이다.

• gcd(1071,1029) = gcd(1029,42) = 21이다.
• gcd(1029,42) = gcd(42,21)
• gcd(42,21) = gcd(21,0)

이를 통해 21이 gcd임을 알 수 있다.

이를 코드로 구현하면

반복문

int gcd(int a,int b){
    while(b!=0){
        int t = a%b;
        a = b;
        b = t;
    }
    return a;
}

재귀함수

int gcd(int a,int b){
    if(b==0)return a;
    return gcd(b,a%b);
}

최소공배수

위의 식에서 A B = GCD(A,B) LCM(A,B)임을 알 수 있다. 이를 통해 LCM(A,B) = A * B / GCD(A,B)로 구할 수 있다.

#include<bits/stdc++.h>
using namespace std;

int gcd(int a,int b){
    while(b!=0){
        int t = a%b;
        a = b;
        b = t;
    }
    return a;
}

int main(){
    int a,b;
    cin>>a>>b;
    cout<<gcd(a,b)<<'\n'<<a*b/gcd(a,b);
}

참고문제 : https://www.acmicpc.net/problem/2609