[프로그래머스] 당구 연습

문제 링크:

https://school.programmers.co.kr/learn/courses/30/lessons/169198

회고:

무식하게 각 케이스별로 거리값 구해서 최솟값 찾도록 했다.
막상 작성하고 나서 보니 어느정도 패턴이 보이는데, 잘하면 일반화 가능할 것 같다.

거리 구하는 팁:

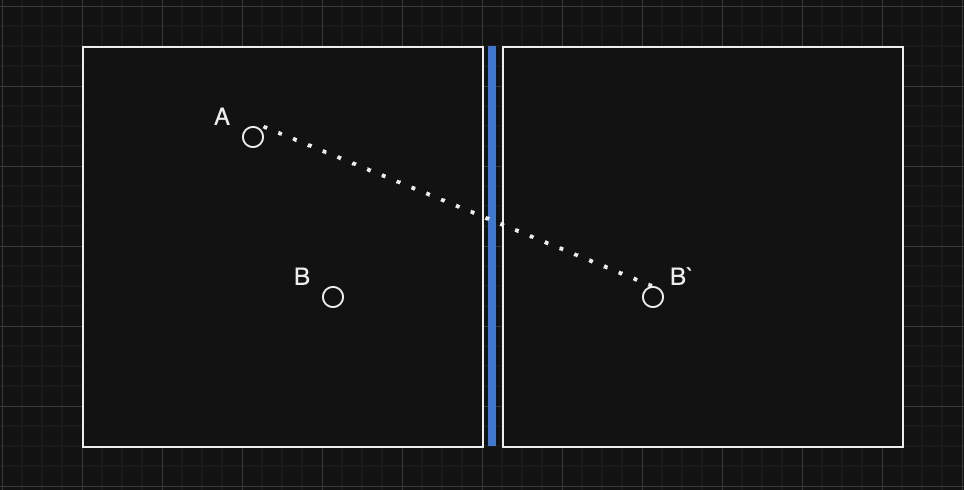
아래와 같이 A -> B으로 오른쪽 벽을 한번 튕겼을때 이동한 거리를 구한다고 한다면.

아래 이미지처럼, B가 오른쪽 축을 기준으로 거울처럼 반사되었다고 생각해보면 된다.
반사된 점 B'와 A사이의 거리를 구하면 된다.

python

def get_square_distance(startX: int, startY: int, endX: int, endY: int) -> int:
    # 두 점 사이 거리 제곱 구하기
    return (endX - startX) ** 2 + (endY - startY) ** 2


def get_minimum_square_distance(m: int, n: int, startX: int, startY: int, endX: int, endY: int) -> int:
    distance = (2 * m) ** 2 + (2 * n) ** 2  # 초기값 설정 (충분히 큰 숫자로)

    """
    벽을 튕기는 케이스
    """
    # 위쪽 벽을 튕긴 경우
    if not (startX == endX and startY < endY):
        distance = min(distance, get_square_distance(startX, startY, endX, 2 * n - endY))

    # 아래쪽 벽을 튕긴 경우
    if not (startX == endX and startY > endY):
        distance = min(distance, get_square_distance(startX, startY, endX, -endY))

    # 오른쪽 벽을 튕긴 경우
    if not (startY == endY and startX < endX):
        distance = min(distance, get_square_distance(startX, startY, 2 * m - endX, endY))

    # 왼쪽 벽을 튕긴 경우
    if not (startY == endY and startX > endX):
        distance = min(distance, get_square_distance(startX, startY, -endX, endY))

    """
    모서리로 튕기는 케이스 (조건 필요: 기울기 동일한지)
    """
    # 왼쪽 위 모서리로 튕기는 경우
    if ((startY - n) / startX == (endY - n) / endX) and not (startX > endX and startY < endY):
        distance = min(distance, get_square_distance(startX, startY, -endX, 2 * n - endY))

    # 오른쪽 위 모서리로 튕기는 경우
    if ((startY - n) / (startX - m) == (endY - n) / (endX - m)) and not (startX < endX and startY < endY):
        distance = min(distance, get_square_distance(startX, startY, 2 * m - endX, 2 * n - endY))

    # 왼쪽 아래 모서리로 튕기는 경우
    if (startY / startX == endY / endX) and not (startX > endX and startY > endY):
        distance = min(distance, get_square_distance(startX, startY, -endX, -endY))

    # 오른쪽 아래 모서리로 튕기는 경우
    if (startY / (startX - m) == endY / (endX - m)) and not (startX < endX and startY > endY):
        distance = min(distance, get_square_distance(startX, startY, 2 * m - endX, -endY))

    return distance


def solution(m: int, n: int, startX: int, startY: int, balls: list) -> list:
    return [get_minimum_square_distance(m, n, startX, startY, ball[0], ball[1]) for ball in balls]


if __name__ == "__main__":
    result = solution(10, 10, 3, 7, [[7, 7], [2, 7], [7, 3]])
    
    print(result)
    print(result == [52, 37, 116])

[52, 37, 116]
True