플로이드 와샬(Floyd Warshall) 알고리즘 구현 (python)

목적 & 특징

• 모든 정점에서 모든 정점으로의 최단 경로를 구한다.
• 다익스트라 알고리즘이 가장 적은 비용부터 하나씩 선택하는 특징이 있는 반면,
  플로이드 와샬 알고리즘은 거쳐가는 정점을 기준으로 알고리즘을 수행하는 특징이 있다.
• 다익스트라 알고리즘은 다이나믹 프로그래밍을 기반으로 한다.

방법

1. 2차원 배열을 만들어서 각 정점에서, 각 정점까지의 비용을 담는다.
   (해당 테이블은 현재까지 계산된 최소 비용을 의미한다. 해당 2차원 배열을 반복적으로 갱신해서 최종적으로는 모든 정점에서 모든 정점으로의 최단 경로를 구하는 것이다. 반복의 기준은 거쳐가는 정점이다.)

2. 노드 1번을 거쳐가는 경우에 대한 최소 경로값을 갱신한다.

   • ex) X→Y 가는 최소 비용 vs X→1 가는 비용 + 1→X 가는 비용
   • 2차원 배열에서 1번 노드가 포함되지 않은 행열에 대해서 위와 같이 비교를 해주면 되며, 더 작은 값으로 갱신한다.

3. 2번을 마지막 노드까지 반복한다.

예시 및 코드(python)

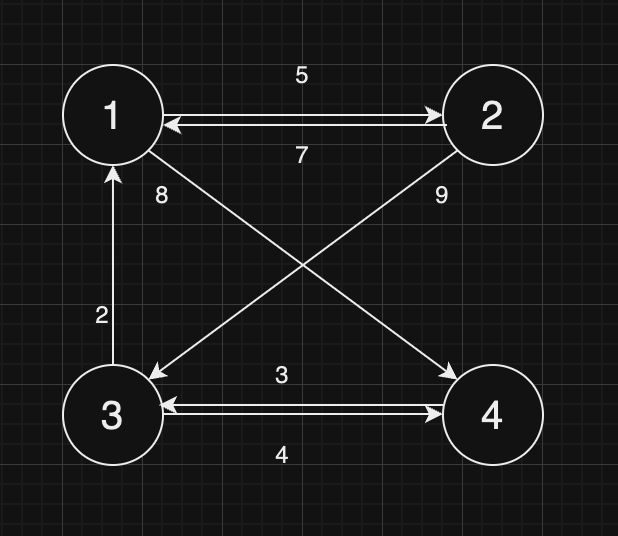
python

def floyd(graph):
    # 노드 개수
    N = len(graph)

    # k: 거쳐가는 노드
    for k in range(N):
        # i: 출발 노드
        for i in range(N):
            # j: 도착 노드
            for j in range(N):
                if graph[i][k] + graph[k][j] < graph[i][j]:
                    graph[i][j] = graph[i][k] + graph[k][j]

    return graph


if __name__ == "__main__":
    INF = 1e8

    graph = [
        [0, 5, INF, 8],
        [7, 0, 9, INF],
        [2, INF, 0, 4],
        [INF, INF, 3, 0]
    ]

    result = floyd(graph)
    for i in result:
        print(i)

[0, 5, 11, 8]
[7, 0, 9, 13]
[2, 7, 0, 4]
[5, 10, 3, 0]

참고 링크

• https://www.youtube.com/watch?v=9574GHxCbKc