서론
알고리즘 대회들을 준비하면서 아직도 숙달되지 않은, 잊어버려서는 안되는 패턴들을 저장해두고자 한다.
일단 대충 적어두고 나중에 Fancy하게 수정하는걸로
본론
동전 DP
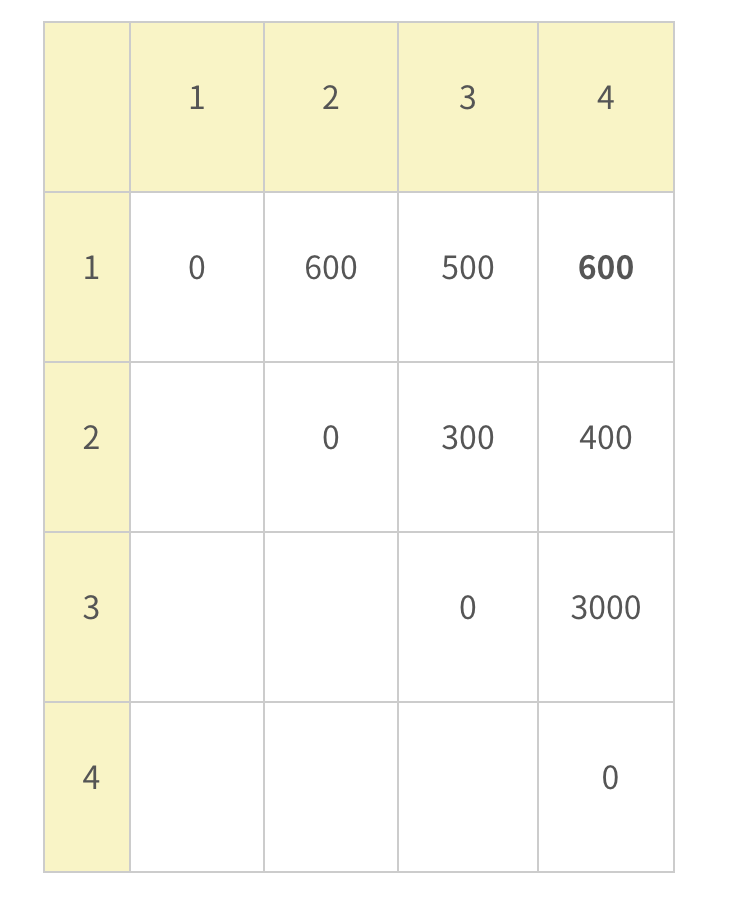
N개의 component로 M을 구성하는 경우의 수 동전 DP
1~N의 component 중 먼저 1번으로 가능한 경우를 다 센다.
그리고 그 1번으로 가능한 경우에 2번으로 가능한 경우를 DP로 세서 더해준다. ex
그러면 1번으로만, 1번과 2번을 섞어서, 2번으로만 가능한 경우들이 모두 나온다.
그렇게 N 개로 모두 다 세어주면 된다.
누적합 imos 법
시작과 끝만 저장해주자는게 idea.
구간들이 여러개 겹치는 상황에서 가장 많이 겹치는 구간을 찾는 문제에서 사용할 수 있음.
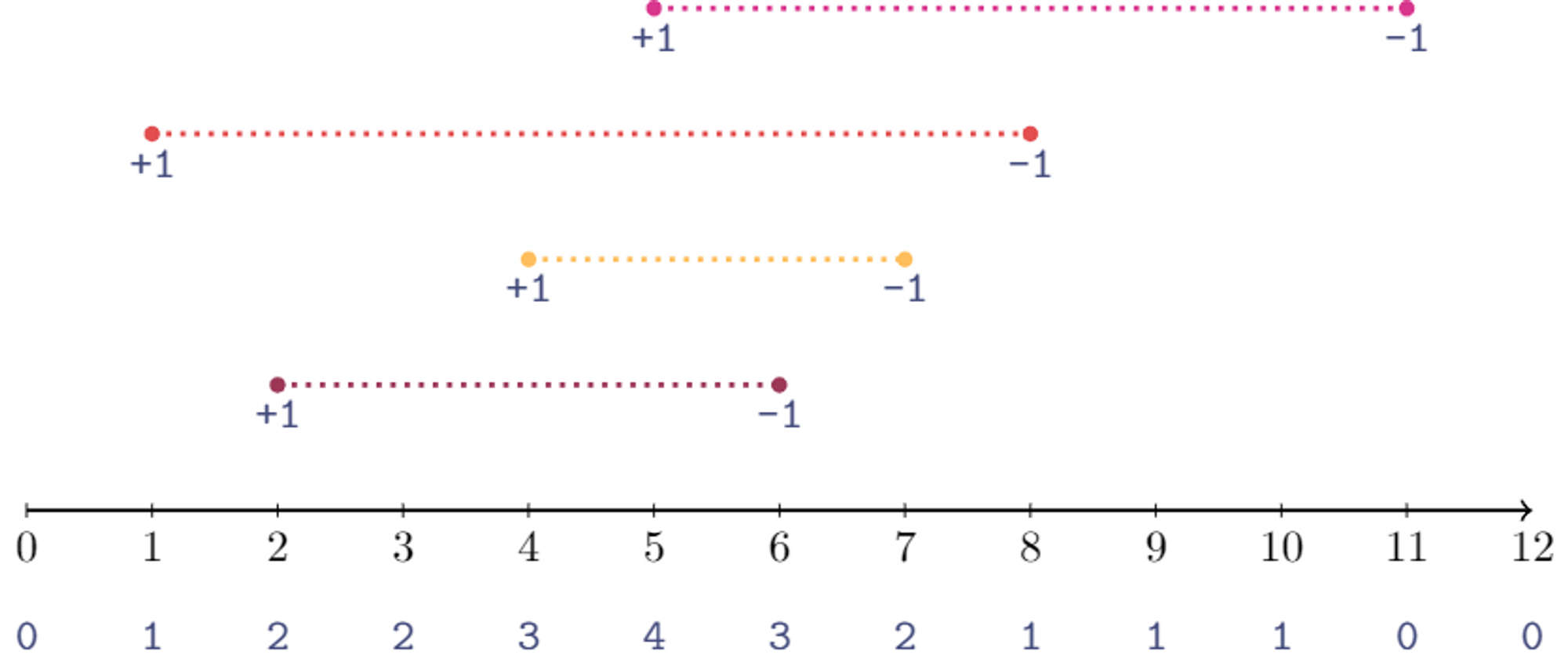
출처 : https://driip.me/65d9b58c-bf02-44bf-8fba-54d394ed21e0
그냥 구하면 줄의 개수 N과 시간선의 길이 T를 곱한 O(NT)의 시간복잡도를 갖게된다.
시간의 시작에 +1, 끝에 -1만 기억해놓고 쭉 시간선을 돌면서 +1을 거칠 떄마다 1을 누적시켜 그 시간선의 값으로 지정해주고 -1일 때 1을 빼서 지정해주면 끝.
-
백준 28018번 시간이 겹칠까?
https://www.acmicpc.net/problem/28018 -
백준 23295번 스터디 시간 정하기1
https://www.acmicpc.net/problem/23295
행렬곱셈 DP
어떤 수열이 주어졌다고 하자. 그 수열의 연산 순서를 달리함에 따라 cost가 달라진다고 하자.
ex)1 2 3 4 5를 2개씩 더할 때 a+b의 cost가 a+b라고 하자.
1+2 = 3, 3+3 =6, 6+4 = 10, 10+5 = 15, 총 cost : 3+6+10+15 = 34
이 때 어떻게 해야 이 cost를 최소화할 수 있는가?
행렬곱셈연산에서는
2x2*2x3*3x5*5x2 라고 할 때 어떤 연산을 먼저 해야 계산을 최소화할 수 있을까? 라는 질문으로 치환할 수 있다.
이를 DP로 생각하자.
예시와 같은 1 2 3 를 더할 때 cost를 최소화하는 문제라면 cut을 생각해보자.
우리는 1 | 2 3, 1 2 | 3의 두 가지 경우만 생각하자는 뜻이다.
1 2 3 4를 더할 때는 1 | 2 3 4, 1 2 | 3 4, 1 2 3 | 4의 세 가지 경우만 생각하자는 뜻이다.
그러면 각각의 조각들을 다시 분해 하고 분해해서 계산하자.
1 | 2 3 4의 2 3 4를 2 | 3 4, 2 3 | 4로. 3 4를 3 | 4로.
그냥 단순히 recursive하게 접근하면 계산이 반복되면 DP로 접근하면 계산횟수를 줄일 수 있다.
Main idea
DP[x][y] == (x부터 y까지의 최솟값)
위를 잘 저장하면 우리의 아이디어인 조각들의 합을 잘 구할 수 있다.
삼중 반복문을 사용해서 구현해야한다.
1번 size 정하기 2번 start 정하기 3번 cut의 위치 정하기
(end는 size에 의해 정해짐)
cut의 위치에 따른 최솟값 code
sub_arr은 부분합을 통해 합을 쉽게 구하기 위함
DP[start][end] = min([DP[start][end],DP[start][cut]+DP[cut+1][end]+sub_sum[end]-sub_sum[start]+arr[start] for cut in range(start,end)])-
시간복잡도는
-
증명 )
-
N이 1000을 넘어가면 못 쓴다.
-
백준 11066번 파일 합치기
https://www.acmicpc.net/problem/11066