Algorithm

Built-in datatype operation

https://wiki.python.org/moin/TimeComplexity
Time complexity

list

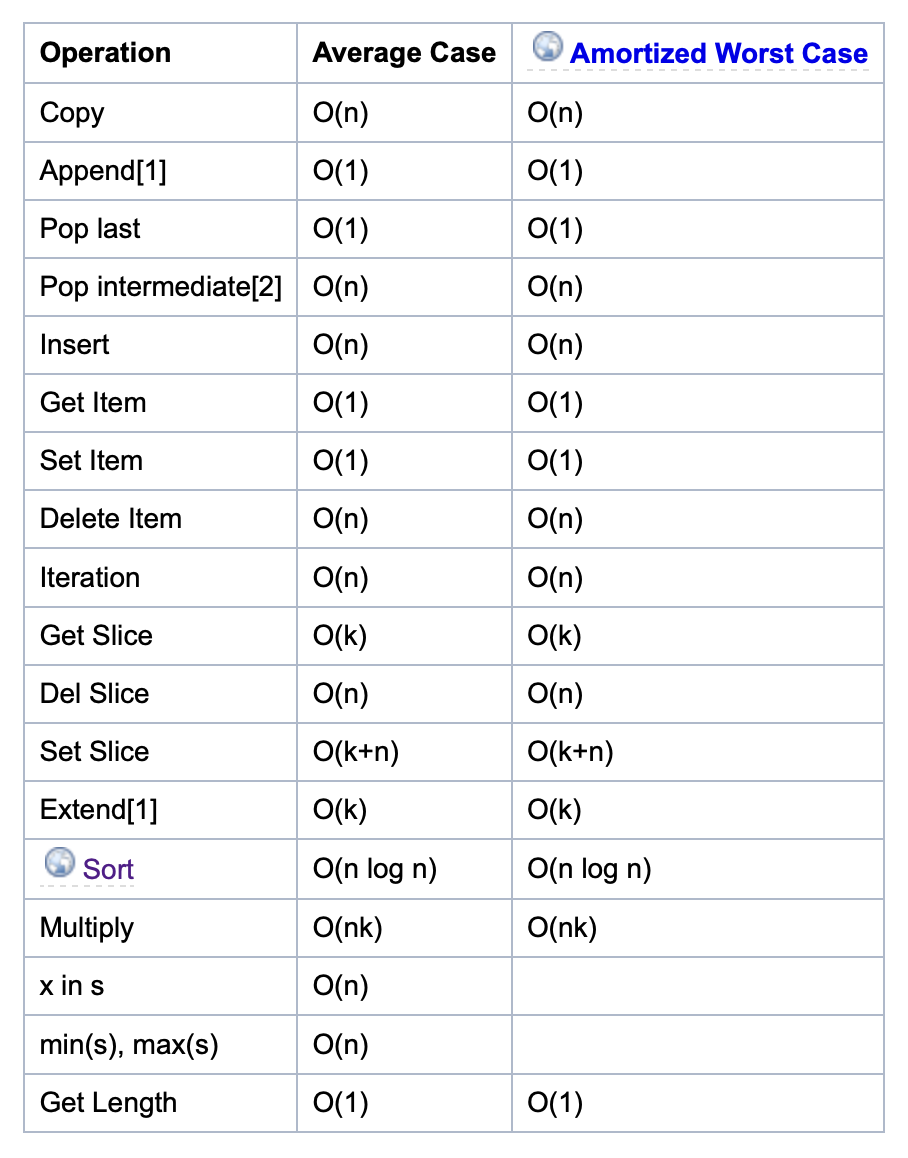
collection.deque

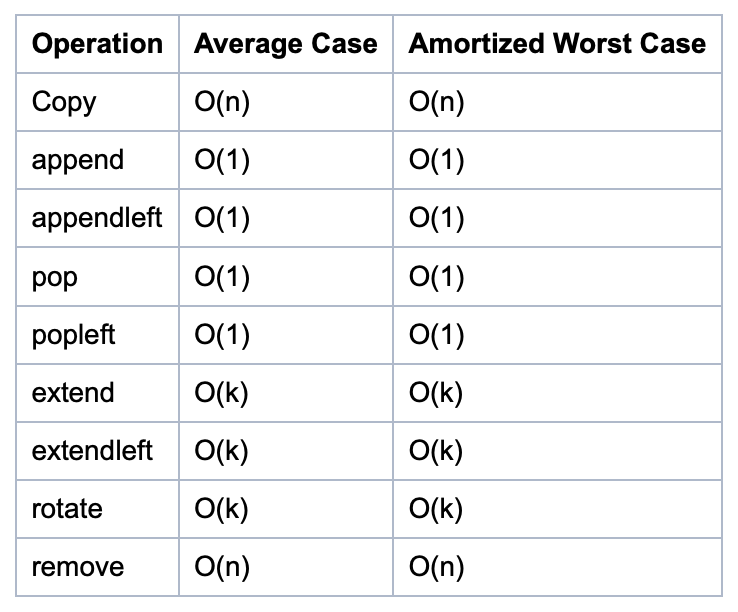
set

hash table

https://baeharam.netlify.app/posts/data%20structure/hash-table
https://stackoverflow.com/questions/7351459/time-complexity-of-python-set-operations

because 'set' is implemented as a hash table, what I need to know for getting in time complexity of 'set' operation is hash table.

dict

Search

unordered linear search

def search(unordered_arr, target):
  for idx, ele in enumerate(unordered_arr):
    if target == ele:
      return idx
      
  return None

arr = [list]
t = [target]
index = search(arr, t)

If array is unordered, there is no choice but searching one by one.

ordered linear search

# given array in ascending order
def search(ordered_arr, target):
  for idx, ele in enumerate(ordered_arr):
    if target == ele:
      return idx
    elif target < ele:
      return None
      
  return None

arr = [list]
t = [target]
index = search(arr, t)

Difference of ordered linear with unordered is ordered linear search can be finished early when target is not in array.

binary search

array should be sorted

def binary_search(ordered_arr, target):
  left, right = 0, len(ordered_arr)-1  
  while left <= right:
    mid = (left+right) // 2
    if ordered_arr[mid] < target:
      left = mid + 1
    elif ordered_arr[mid] > target:
      right = mid - 1
    else:
      return mid
      
  return None

arr = [list]
t = [target]
index = binary_search(arr, t)

bisect module

The module is called bisect because it uses a basic bisection algorithm to do its work

bisect_left
-> Locate the insertion point for x in a to maintain sorted order.

import bisect

def bisect_search(ordered_arr, target):
  index = bisect.bisect_left(ordered_arr, target)
  
  if index < len(ordered_arr) and ordered_arr[index] == target:
    return index
  else:
    return None

arr = [list]
t = [target]
index = binary_search(arr, t)

Divide and Conquer

hanoi

def hanoi(num, start, dest, extra):
    # base
    if num == 1:
        hanoi.count += 1
        print(f'a disk is moved from {start} into {dest}')
        return
    
    # general
    hanoi(num-1, start, extra, dest)
    hanoi.count += 1
    print(f'a disk is moved from {start} into {dest}')
    hanoi(num-1, extra, dest, start)


hanoi.count = 0
hanoi(
    num=3,
    start=1,
    dest=3,
    extra=2
)
print(hanoi.count)

Complexity: O(2^n)

f(n)
= 2f(n-1) + 1
= 2^2f(n-2) + 2 + 1
...
= 2^(n-1)f(1) + 2^(n-1) - 1

note

hanoi.count
It can be understood in point of 'class variable', even hanoi is not a class. I believe kind of this declaration is not recommended.

Brute force

all-case-search

exhaustive search

# recursive implementation
def bit_str(ans, n=3):
  if len(ans) == n:
    print(*ans)
  
  for ele in data:
    ans.append(ele)
    bit_str(ans)
    ans.pop()


data = 'abc'
bit_str([])

Backtracking

permute

good implementation

def permute(arr, num):
    if len(arr) == num:
        print(*arr)
    
    for n in range(1, num+1):
        if n in arr:
            continue
        arr.append(n)
        permute(arr, num)
        arr.pop()


arr = []
num = 3
permute(arr, num)

bad implementation

# this code occured
# RecursionError: maximum recursion depth exceeded while calling a Python object
def permute(arr, num):
    if len(arr) == num:
        print(*arr)
    
    for n in range(1, num+1):
        if not n in arr:
            arr.append(n)
        permute(arr, num)
        arr.pop()


arr = []
num = 3
permute(arr, num)

not과 continue, 둘 다 중복되는 원소를 넣지 않기 위해서 쓰였지만, 코드가 읽히는 경로가 달라짐으로 인해 한 쪽은 실행이 되고 다른 한 쪽은 실행이 되지 않는다.

combine

Combination: NCn

def combine(arr, N, num):
    if len(arr) == num:
        print(*arr)
    
    for n in range(1, N+1):
        if arr and n <= arr[-1]:
            continue
        arr.append(n)
        combine(arr, N, num)
        arr.pop()


arr = []
N, num = 4, 2
combine(arr, N, num)

Data Structure

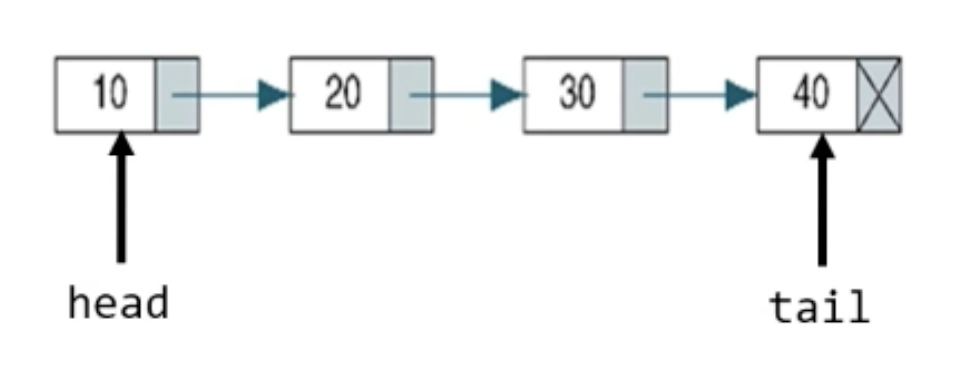
Linked list

vs python list

pros

• they dont require sequential storage space
• you can start smart small and grow arbitrarily as you add more nodes
• it can fastly operate in insert, delete

cons

• additional space to store address

class Node:
    def __init__(self, data) -> None:
        self.data = data
        self.next = None

class SinglyLinkedList:
    def __init__(self) -> None:
        self.head = None
        self.size = 0
    
    # for insertion, use pre_node
    def insert(self, pre_node, data):
        node = Node(data)
        self.size += 1
		
        # not empty and not head
        if pre_node:
            node.next = pre_node.next
            pre_node.next = node
        # empty or head
        else:
            node.next = self.head
            self.head = node
    
    def traverse(self):
        current = self.head
        while current:
            yield current.data
            current = current.next
    
    def delete(self, pre_node):
        self.size -= 1
		
        if pre_node:
            pre_node.next = pre_node.next.next
        else:
            self.head = self.head.next

Circular list

class Node:
    def __init__(self, data) -> None:
        self.data = data
        self.head = None

class CircularList:
    def __init__(self) -> None:
        self.head = None
        self.size = 0
    
    def insert(self, pre_node, data):
        node = Node(data)
        self.size += 1
		
        # not empty
        if pre_node:
            node.next = pre_node.next
            pre_node.next = node
            
        # empty
        else:
            self.head = node
            node.next = node
    
    def traverse(self):
        current = self.head
        while current:
            yield current.data
            current = current.next
            if current is self.head:
                break

    def delete(self, pre_node):
        self.size -= 1
		
        # not head
        if pre_node.next != self.head:
            pre_node.next = pre_node.next.next
        
        # head
        else:
        	# only one element list
            if self.head is pre_node:
                self.head = None
            
            # multiple nodes
            else:
                self.head = self.head.next
                pre_node.next = self.head

algorithm example

Josephus
baekjoon link

baekjoon 1648ms

from circularlist import CircularList

N, K = map(int, input().split())
circle_list = CircularList()

for n in range(N, 0, -1):
    circle_list.insert(circle_list.head, n)
# circle_list.head = circle_list.head.next
current = circle_list.head

# look over list
# for node in circle_list.traverse():
#     print(node, end=' ')

print('<', end='')
for _ in range(N-1):
    prev = current
    for _ in range(K-1):
        prev = prev.next    
    current = prev.next
    circle_list.delete(prev)
    print(current.data, end=', ')
print(circle_list.head.data, end='>')

baekjoon 1172ms

def reaching_node(circle_list, num):
    current = circle_list.head
    for _ in range(1, num):
        current = current.next
    return current


cc_list = CircleList()
n, m = map(int, input().split())

# create circle_list
for i in range(n, 0, -1):
    cc_list.insert(cc_list.head, i)
print("<", end='')

# 요세푸스 순열; except last node
for _ in range(1, n):
    data = reaching_node(cc_list, m)
    print(data.next.data, end=', ')
    cc_list.head = data
    cc_list.delete(data)
print(cc_list.head.data, end='>')

my old anwser is more optimum...

Stack & Queue

Stack

Stack Operation

• push
• pop

Queue

Queue Operation

• enqueue
• dequeue