[T-test]
t-테스트는 일반적으로 검정통계량의 정규 분포를 따르며 분포와 관련된 스케일링 변숫값들이 알려진 경우에 사용한다.
집단간 차이 분석으로 평균 또는 비율 차이를 분석한다.
독립변수 : 범주형 , 종속변수 : 연속형
t분포를 사용하는 경우, 표본 평균을 이용하여 정규 분포의 평균을 해석할때 사용한다
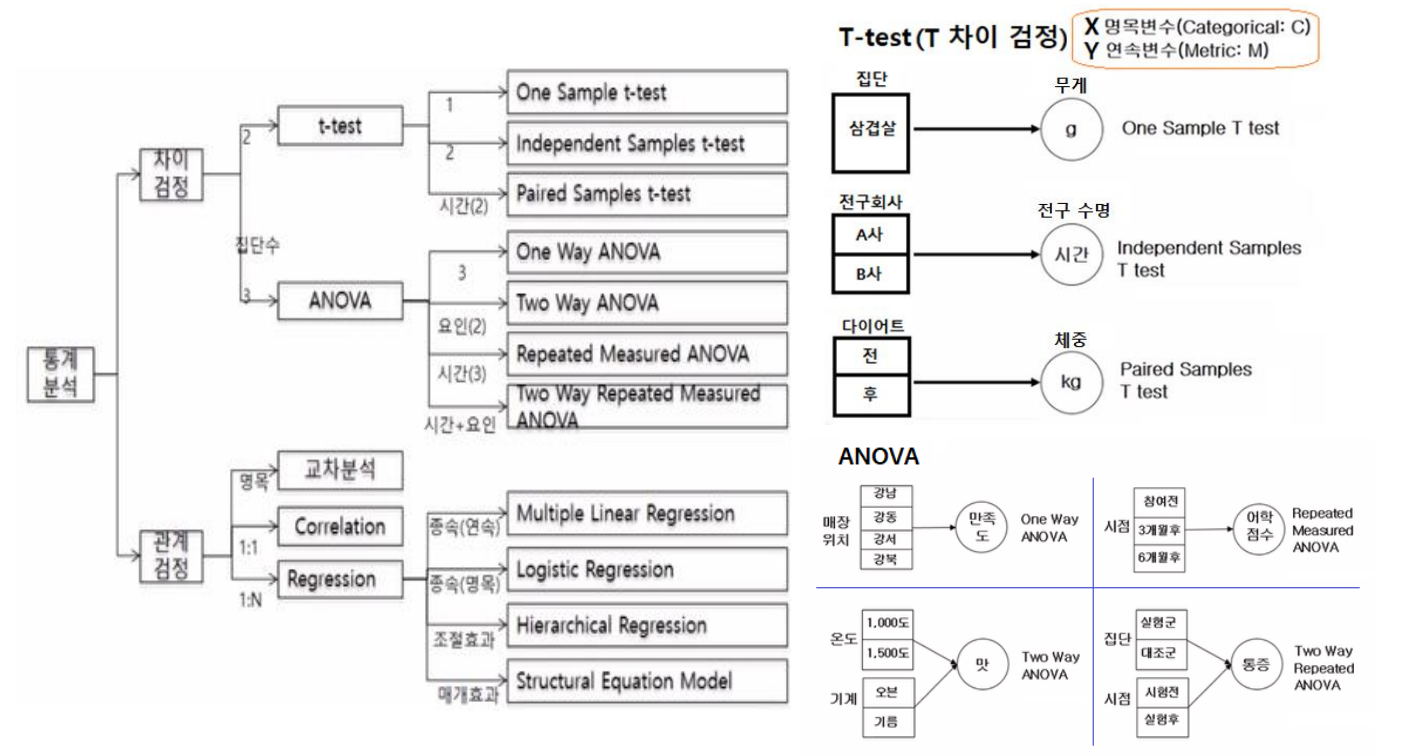
-
집단이 1개일때 T-Test :
One Sample T test -
집단이 2개일때 T-Test :
Independent Samples T test -
집단이 2개, 시간에 따른 변화를 분석 T-Test :
Paired Samples T test -
집단이 3개 이상일땐 ANOVA : 다음 포스트에서 작성 예정
- T-test와 ANOVA의 차이
- 두 집단 이하의 변수에 대한 평균차이를 검정할 경우 T-test를 사용하여 검정통계량 T값을 구해 가설검정을 한다.
- 세 집단 이상의 변수에 대한 평균차이를 검정할 경우에는 ANOVA를 이용하여 검정통계량 F값을 구해 가설검정을 한다.
두 개 이하의 집단 비교를 위한 평균과 표준 편차 비율의 차이를 구하고,
그 차이가 우연이냐 아니냐를 판단하는 검정방법이다.
one samples t-test
단일 모집단의 평균에 대한 가설검정이라고 하며,
정규분포에 대해 기댓값을 조사하는 검정 방법이다.
-
[귀무] H0 : 표본의 평균 (x) = 모집단 평균(μ,x̄)
표본의 평균 - 모집단평균 = 0 -
[대립] H1 : 표본의 평균 (x) ≠ 모집단 평균(μ,x̄)
표본의 평균 - 모집단평균 > 0 또는 < 0
하나의 집단에 대한 표본 평균이 예측된 평균과 같은지 여부를 확인한다.
예제 1
어느 남성 집단의 평균 키 검정.
귀무 : 집단의 평균키가 177이다.
대립 : 집단의 평균키가 177이 아니다.
[167.0,162.9,169.2,176.7,187.5]one_sample = [167.0,162.9,169.2,176.7,187.5]
print(np.mean(one_sample)) #172.66
result = stats.ttest_1samp(one_sample,popmean=177)
print('statistic : %.3f, pvalue:%.3f'%result) stats.ttest_1samp()함수를 사용한다.- 해석
statistic : -1.001, pvalue:0.373- pvalue:0.373 > 0.05 이므로 귀무 채택.
해당 데이터는 유의미한 차이가 아님. 집단의 평균키는 177이다.
예제 2
실습 예제 2)
A중학교 1학년 1반 학생들의 시험결과가 담긴 파일을 읽어 처리 (국어 점수 평균검정)
귀무 : A중학교 1반 학생들의 국어점수 평균은 80 이다.
대립 : A중학교 1반 학생들의 국어점수 평균은 80이 아니다data = pd.read_csv("../testdata/student.csv")
print(data['국어'].mean()) #72.9
result2 = stats.ttest_1samp(data['국어'],popmean=80)
print('statistic : %.3f, pvalue:%.3f'%result2) - 해석
statistic : -1.332, pvalue:0.199- pvalue : 0.199 > 0.05 이므로 귀무 채택.
A중학교 1반 학생들의 국어점수 평균은 80 이다.
independent samples t-test
-
서로 독립인 두 집단의 평균 차이 검정.
남녀의 성적, A반과 B반의 키, 경기도와 충청도의 소득 따위의 서로 독립인 두 집단에서 얻은 표본을 독립표본(two sample)이라고 한다. -
sample이 2개일때 t검정값을 구하는 방법.
-
선행조건 : 두 집단을 정규분포를 따라야 한다. 두 집단의 분산이 동일하다는 가정이 필요함
-
t-value = (평균1-평균2)/(표준편차/표본개수 제곱근)
예제1
실습) 남녀 두 집단 간 파이썬 시험의 평균 차이 검정
남녀 두 집단 간 파이썬 시험의 평균차이가 11점정도 나는데 우연히 발생할 확률은 얼마인가?
만약 우연히 발생했다면 평균은 같은것이고 우연이 아니면 다른것이다.- 귀무 : 남녀 두 집단 간 파이썬 시험 평균의 차이가 없다
- 대립 : 남녀 두 집단 간 파이썬 시험 평균의 차이가 있다.
male = [75, 85, 100, 72.5, 86.5]
female = [63.2, 76, 52, 100, 70]
print(np.mean(male),np.mean(female)) #83.8 72.24 (11점차이)
two_sample = stats.ttest_ind(male,female, equal_var=True) #등분산성을 띄고있다 가정
print(two_sample) #statistic=1.233, pvalue=0.252- 결론
- pvalue(0.25) > 0.05 이므로 귀무 채택
- 남녀 두 집단 간 파이썬 시험의 평균의 차이가 없다. 우연히 발생한 자료임
예제2
- 실습) 두 가지 교육방법에 따른 평균시험 점수에 대한 검정 수행 two_sample.csv (데이터가공)
data = pd.read_csv("../testdata/two_sample.csv")
print(data.head(3))
# 교육방법 / 점수
ms = data[['method','score']]
m1 = ms[ms['method']==1]
m2 = ms[ms['method']==2]
score1 = m1['score']
score2 = m2['score']
#결측치를 평균으로 채우기
sco1 = score1.fillna(score1.mean())
sco2 = score2.fillna(score2.mean())
result = stats.ttest_ind(sco1,sco2)
#statistic=-0.1964, pvalue=0.8450- 선행조건1) 정규성 확인 : 두 집단은 정규분포를 따라야 한다.
shapiro test
# 시각화로 정규성 확인
import matplotlib.pyplot as plt
import seaborn as sns
sns.histplot(sco1,kde=True)
sns.histplot(sco2,kde=True)
plt.show()
#shapiro test
#pvalue = 0.05보다 커야 만족. 정규성 확인 함수
print(stats.shapiro(sco1).pvalue) #pvalue=0.3679
print(stats.shapiro(sco2).pvalue) #pvalue=0.6714
-
선행조건2) 등분산성 확인 : 두 집단의 분산이 동일하다는 가정이 필요. (p>.0.05 면 만족)
stats.levene: 모수검정stats.fligner: 모수검정. levene과 유사stats.bartlett: 비모수검정
-
모수와 비모수
모수 검정이란?: 특정 표본에서 평균, 표준편차, 분산등의 몇가지 지표(parameter)를 뽑아, 특정 집단 사이의 특징을 비교하는 검정 방법비모수검정이란?: 모수에 대한 가정을 전제로 하지 않고 모집단의 형태와 관계없이 주어진 데이터에서 직접 확률을 계산하여 통계적으로 검정하는 분석 방법
print(stats.levene(sco1,sco2).pvalue) # 0.4568
print(stats.fligner(sco1,sco2).pvalue) # 0.4432
print(stats.bartlett(sco1,sco2).pvalue) # 0.2678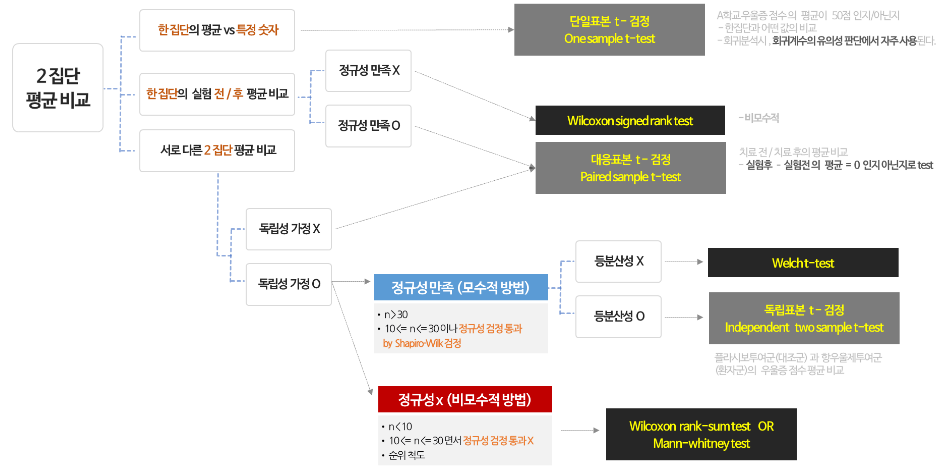
그 후 분석결과를 도출해내기 위한 함수를 사용해야하는데,
정규성과 등분산성, 샘플크기에 따라 사용되는 함수가 다르다.
- 정규성 만족
- 등분산성 만족시 :
stats.ttest_ind(sco1,sco2,equal_var=True) - 등분산성 불만족시 :
stats.ttest_ind(sco1,sco2,equal_var=False)
- 등분산성 만족시 :
- 정규성 불만족
- 두 집단의 샘플크기가 같은경우 :
stats.wilcoxon(sco1,sco2) - 두 집단의 샘플크기가 다른경우 :
stats.mannwhitneyu(sco1,sco2)
- 두 집단의 샘플크기가 같은경우 :
예제3
어느 음식점 매출데이터, 날씨데이터를 활용하여 강수 여부에 따른 매출의 평균차이 검정- 귀무 : 강수여부에 따른 매출액의 평균에 차이가 없다.
- 대립 : 강수여부에 따른 매출액의 평균에 차이가 있다.
- 데이터가공
- 매출데이터와 날씨데이터 읽기
- 날짜를 기준으로 병합하기
# 매출데이터 읽기
sales_data = pd.read_csv("../testdata/tsales.csv",dtype={'YMD':'object'}) #AMT 매출액
# 날씨데이터 읽기
wt_data = pd.read_csv("../testdata/tweather.csv") #sumRn 강수량
wt_data['tm'] = wt_data['tm'].map(lambda x:x.replace('-',''))
# 두 데이터 병합
frame = sales_data.merge(wt_data,how='left',left_on='YMD',right_on='tm')
data = frame.iloc[:,[0,1,7,8]] # YMD/AMT/maxTa(최고기온)/sumRn(강수량)- 특성에 따른 집단으로 나누고 시각화
data['rain_yn'] = (data['sumRn']>0).astype(int) #강수유무 컬럼 추가. (0/1)
print(data)
#강수량 있는 집단,없는 집단 분리
import matplotlib.pyplot as plt
sp = np.array(data.iloc[:,[1,4]]) #AMT,rain_yn 2차원배열
tg1 = sp[sp[:,1]==0,0] # 집단1 : 강수유무가 0인 모든행 (강수량없음)
tg2 = sp[sp[:,1]==1,0] # 집단2 : 강수유무가 1인 모든행 (강수량있음)
plt.boxplot([tg1,tg2],notch=True,meanline=True,showmeans=True)
plt.show()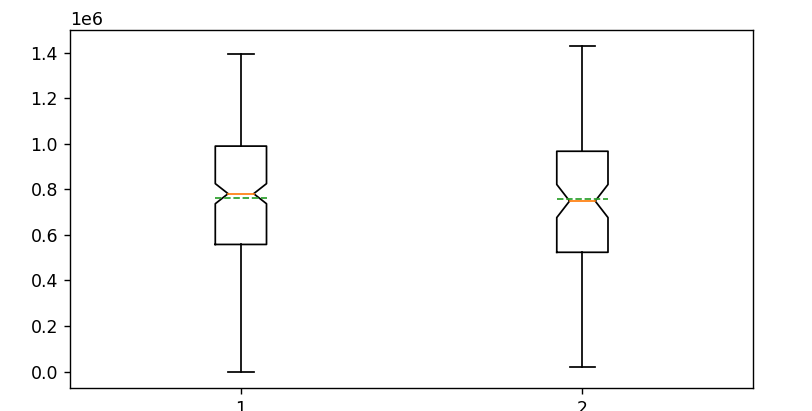
boxplot에서 평균 점선에 약간에 차이가 보인다. 이는 수치상 약 3700의 차이인데,
이 차이가 유의미한 차이인지 분석을 해보자.
- 분석
# 정규성 확인 (N > 30)
print(len(tg1),len(tg2)) #236 92
print(stats.shapiro(tg1).pvalue) #0.0560
print(stats.shapiro(tg2).pvalue) #0.8827
# 등분산성 확인
print(stats.levene(tg1,tg2).pvalue) #0.7123
# 모두 0.05보다 크므로 만족. ttest_ind 사용
print(stats.ttest_ind(tg1,tg2,equal_var=True))- Ttest_indResult : statistic=0.1010, pvalue=0.9195
- 해석 : 정규성,등분산성은 조건을 충족했다.
pvalue(0.919) > 0.05 이므로, 귀무가설이 채택
paired samples t-test
처리 이전과 처리 이후를 각각의 모집단으로 판단하여,
동일한 관찰 대상으로부터 처리 이전과 처리 이후를 1:1로 대응시킨 두 집단으로 부터의 표본을 대응표본(paired sample)이라고 한다.
대응인 두 집단의 평균 비교는 동일한 관찰 대상으로부터 처리 이전의 관찰과 이후의 관찰을 비교하여 영향을 미친 정도를 밝히는데 주로 사용하고 있다.
집단 간 비교가 아니므로 등분산 검정을 할 필요가 없다.
예제1
실습) 복부 수술 전 9명의 몸무게와 복부 수술 후 몸무게 변화
baseline = [67.2, 67.4, 71.5, 77.6, 86.0, 89.1, 59.5, 81.9, 105.5]
follow_up = [62.4, 64.6, 70.4, 62.6, 80.1, 73.2, 58.2, 71.0, 101.0]4
(두 데이터의 평균 차이는 약 6.91이다)- 귀무 : 복부 수술 전 몸무게와 복부 수술 후 몸무게 변화에 차이가 없다.
- 대립 : 복부 수술 전 몸무게와 복부 수술 후 몸무게 변화에 차이가 있다.
stats.ttest_rel 를 사용한다.
paired_sample = stats.ttest_rel(baseline,follow_up)
print(paired_sample) #statistic=3.668, pvalue=0.0063
# 결론 : pvalue:0.006 < 0.05 이므로 귀무가설 기각.
# 몸무게 변화에는 차이가 있다.참고
reference : (https://cafe.daum.net/flowlife/SBU0/43)
