데이터 분석 및 검정 방법 구분
- 각 데이터 특성에 대한 분석방법
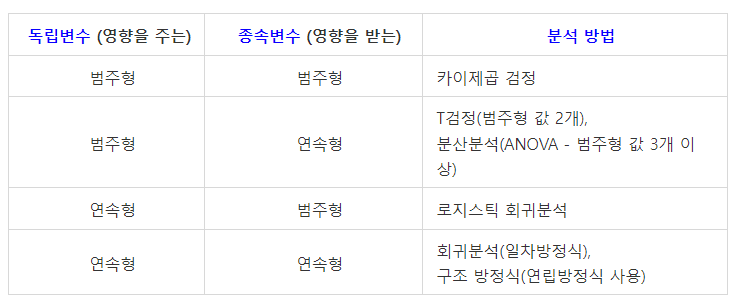
카이제곱검정은 구간 별로 관측된 빈도와 기대 빈도의 차이를 살펴보고, 확률모형이 얼마나 자료를 잘 설명하는지를 알려준다.
카이제곱검정의 3가지 목적
1) 독립성 검정 : 두 범주형 변수 간에 관련성이 있는지 여부를 알고자 할 때 사용.
2) 적합도 검정 : 두 데이터가 특정한 분포에서 추출된 것인가를 알고자 할 때 사용.
2) 동질성 검정 : 두 개 이상의 다항분포가 동일한지 여부를 알고자 할 때 사용.
가설검정
가설검정의 대략적인 방식은 먼저 특정 가설을 세우고, 해당 가설이 옳다고 가정한 뒤 ‘확률적으로는 거의 일어나지 않을 일’이 일어나면 그 가설을 부정하고 반대의 가설을 채택하는 것이다.
즉, 가설 X가 올바르다고 가정했을 때, 확률적으로 일어날 수 없는 아주 희귀한 일이 일어난다면 가설 X 자체가 잘못되었을 가능성이 크다는 것으로, 최초의 가설 X를 부정하고 남은 가설 Y를 채택한다는 원리라 할 수 있다.
- 수학적 검증
- 통계적 추론 -> 대립가설 / 귀무가설
- 귀무가설
일반적으로 맞다고 가정하는가설.
현재의 정설(가설)로 관습적, 보수적 주장.
새 가설에 의해 대체될 것을 예상하는 가설 - 대립가설
새롭게 맞다고 증명하려는 가설.
귀무가설에 대립되는 설로 새롭게 검정하고자 하는 주장.
적극적으로 입증하고자 하는 주장
- 귀무가설
어느정도의 에러가 있을 수 있는 가설검정은
100% 검증이 되어야 하는 수학적 검증과는 약간 거리가 있다.
귀무가설은 더이상 검정 할 이유가 없는 0가설이다. (H0) (이미 정설이기 때문)
이에 대립되는 대립가설은 H1 또는 Ha
- 가설검정 시에 이 두 개의 가설은 정반대로 설정되어야 한다.
예) 서로 같다 - 서로 같지 않다- 집단1의 분산이 더 크다 - 집단1의 분산이 더 작거나 같다
- 집단1의 비율이 더 크다 - 집단1의 비율이 더 작거나 같다
논문이나 보고서에서는 귀무가설을 기각하고, 대립가설을 채택하는 것이 목적이다.
가설 검정 정리 : https://kkokkilkon.tistory.com/36
P값(P-value, 유의확률)
p-값은 귀무가설을 기각할 수 있는 최소한의 확률 값으로
데이터 내 H0에 반하는 증거의 강도.
예를 들어 귀무가설과 대립가설 중에서, 귀무가설이 더 옳다면 귀무가설을 채택해야 한다.
하지만 오차에 의해서 "귀무가설이 더 옳은데도 불구하고, 귀무가설을 탈락시키는 확률”이 생기는데, 이를 α(알파)라고 부른다.
(확률 α를 “유의수준”이라고 부르는데, 보통 1%, 5%, 10%를 많이 사용한다. 데이터의 경중에 따라 다름.)
분석에는 2가지 방법이 있다.
- 분석1 (통계분석도구)
- α > p-value 귀무기각 : 새로운 대립가설이 채택
- α < p-value 귀무채택 : 새로운 대립가설을 기각
- 분석2 (chi제곱 분포, t분포 등)
- 얻어낸 임계치가 검정통계량 표를 통해 검정통계량 안에있는지 밖에있는지에 대해 여부를 판단.
새로운 대립가설에서 비롯된 p-value값이 귀무가설을 탈락시키는 확률(α)보다 우수한 수치가 나오니, 귀무가설이 기각될수밖에 없는것.
검정 통계량
확률의 총합은 1이기 때문에,
귀무가설이 더 옳기에, 귀무가설을 채택할 확률”은 1-α가 된다. 그래서 1-α는 귀무가설을 채택시키므로, 1-α의 영역을 “채택역”이라고 부르고, 반대로 α는 귀무가설을 기각(탈락)시키므로, α의 영역을 “기각역”이라고 부른다.
이 통계그래프의 형태에서 기각역은 양측검정이 될수도, 단측검정이 될 수도 있다.

결론적으로, 이 채택역과 기각역으로 귀무가설의 채택과 기각여부를 판단하는데, 이때 검정통계량을 활용한다.(구간을 나누는 직선은 임계치라고 한다.)
이 검정 통계량이 채택역 안에 위치한다면 귀무가설채택.
기각역 안에 위치하면 귀무가설은 기각된다. 대립가설은 정반대로 판단하면 된다.
reference : https://math100.tistory.com/75
Type error
-
1종 오류 (Type I error):
귀무가설(H0)이 실제로는 참이어서 채택해야 함에도 불구하고 표본의 오차때문에 이를 채택하지 않는 오류. 보통 α (알파)로 표기하고 유의수준이라고 부름. -
2종 오류 (Type II error):
귀무가설(H0)이 거짓이라서 채택하지 말아야 하는데 표본의 오차 때문에 이를 채택하는 오류. 보통 β (베타)로 표기.
reference : https://drhongdatanote.tistory.com/76
주로 1종 오류를 중요시 여기고 있다.
