57fvoh4
Exclusive OR, Exclusive NOR
XOR
배타적 논리합
2개의 입력이 서로 다르면 1, 같으면 0
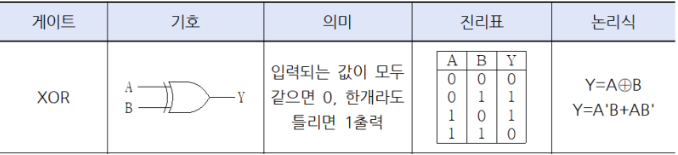
논리 회로
Y = A`B + AB`

XNOR
배타적 부정 논리합
XOR게이트와 NOT게이트를 합한것과 같은 출력
2개의 입력이 서로 다르면 0, 같으면 1
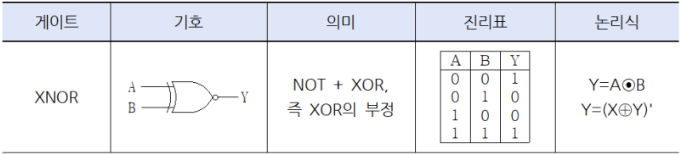
논리 회로
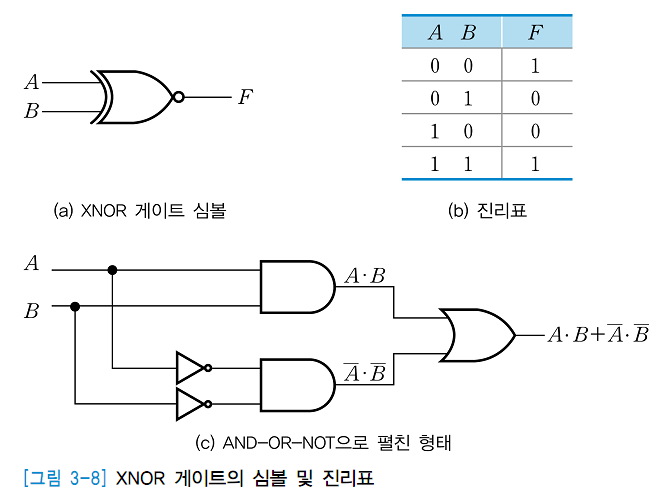
XOR의 출력에 NOT게이트만 붙여도 XNOR의 출력값이 나온다, 하지만 결선만 바꿔도 XNOR를 만들수 있기때문에 NOT게이트를 하나 더 쓰는것보단 결선을 바꾸는것이 더 좋은 방법이라고 할 수 있다.
부울 대수와 드 모르강의 정리

부울대수를 이용한 간소화
| A | B | C | X |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
ex) X = A`B`C` + A`B`C + A`BC + AB`C + ABC
동일 법칙 A + A = A 이용 A`B`C 추가 따라서 A`B`C + A`B`C = A`B`C 변한건 없음
X = A`B`(C`+C)+A`C(B`+B)+AC(B`+B) = A`B`+A`C+AC = A`B`+C(A`+A) = A`B`+C
회로
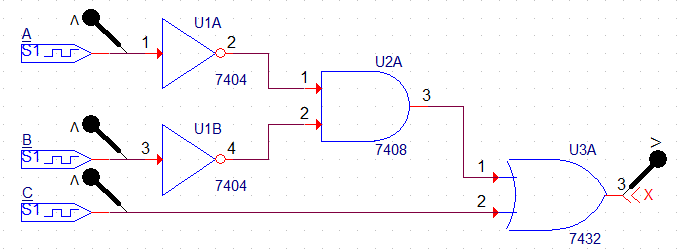
결과
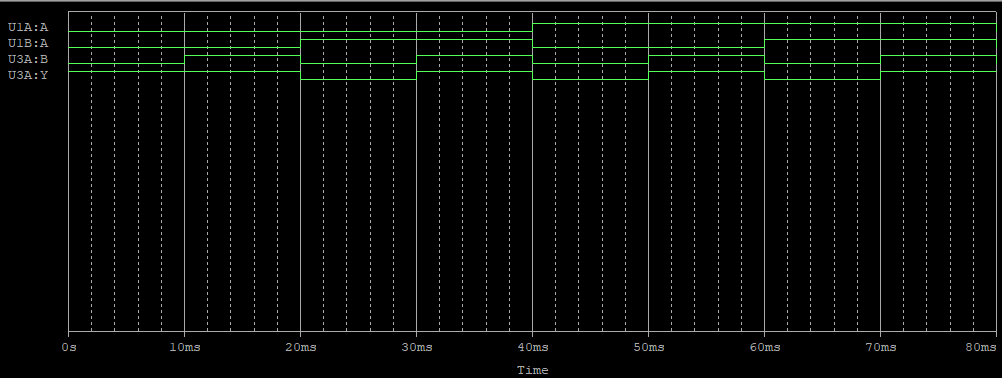
드 모르강의 정리
- 각 변수를 부정(NOT)한 것의 OR는 NAND와 같다. A`+B`=A`B`
- 각 변수를 부정(NOT)한 것의 AND는 NOR와 같다. A`B`=(A+B)`
ex) X=A`B`+C = (A+B)`+C
회로
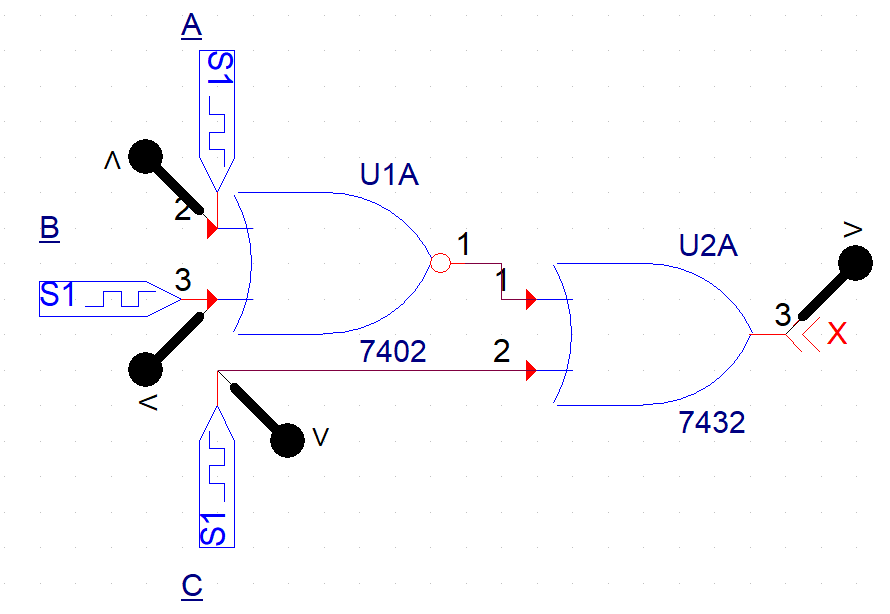
결과
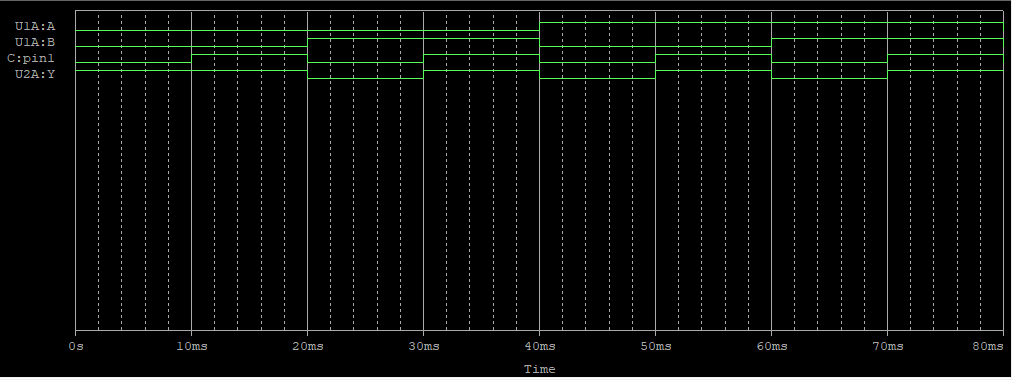
진리표와 진리표의 논리식을 부울 대수로 간소화한 논리식과 그것을 드모르강의 정리로 바꾼 논리식
모두 같은 결과과 나옴
카르노 맵
논리식 간소화 방법
카르노맵에 변수를 표시할때는 변수로 A`B 또는 2진수로 01 이런식으로 표시한다
표시하는 변수들은 옆칸으로 갈때마다 1비트씩만 변한다 01->11(01->10은 2비트가 변한것)
1. 논리식의 각 항(진리표의 출력1이되는 변수들)을 카르노 맵에 1로 표시한다
2. 1이 표시된 칸을 직사각형 또는 정사각형으로 묶는다(이때 1이 2의 제곱수로 포함되게 묶는다...2, 4, 8, 16...), 묶을때 한번에 많이 묶을 수 있으면 그렇게 하는것이 논리식을 더 간소화 할 수 있다, 다른것에 이미 묶여있는 1이라도 중복으로 겹쳐서 포함해서 묶는것도 가능하다
3. 묶인 부분에서 논리 레벨이 변하는 변수를 삭제한다.
4. 남겨진 변수에 따른 논리식을 OR하여 간소화된 논리식을 만든다
| A | B | C | D | X |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
A̅B̅CD̅ + A̅B̅CD + A̅BCD̅ + A̅BCD + ABC̅D̅ + ABC̅D + ABCD̅ + ABCD
Y = AB + A`C
회로
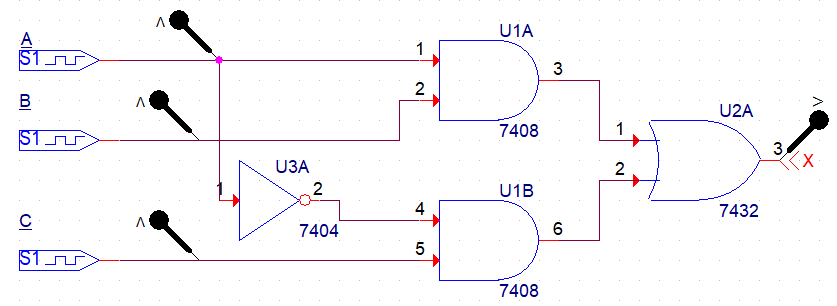
결과
조합 논리회로
가산기와 감산기
가산기와 감산기는 2진수를 더하거나 빼는 디지털 회로이다. 가산기는 보수를 이용하여 감산을 할 수 있고, 자리옮김(Shift)으로 곱하기나 나누기도 할 수 있다. 이 때문에 감산기보다 가산기를 더 많이 사용된다
가산기
가산기는 두 개의 2진수를 더하는 동작을 한다. 이때 비트끼리의 합과 자리올림 출력(Carry Out)이 생긴다, 윗자리에서는 이를 자리올림 입력(Carry In)이라 한다.
반가산기
반가산기(Half Adder)는 합 S와 지리올림 출력 Co만 출력하며, 자리올림 입력을 받을 수 없다
캐리는 입력이 모두 1인경우에만 1이되고 합은 입력중 하나만 1이여도 1이된다

전가산기
전가산기는 두 개의 반가산기로 구성되며, 입력으로 자리올림 입력 Ci가 포함되어 있다.

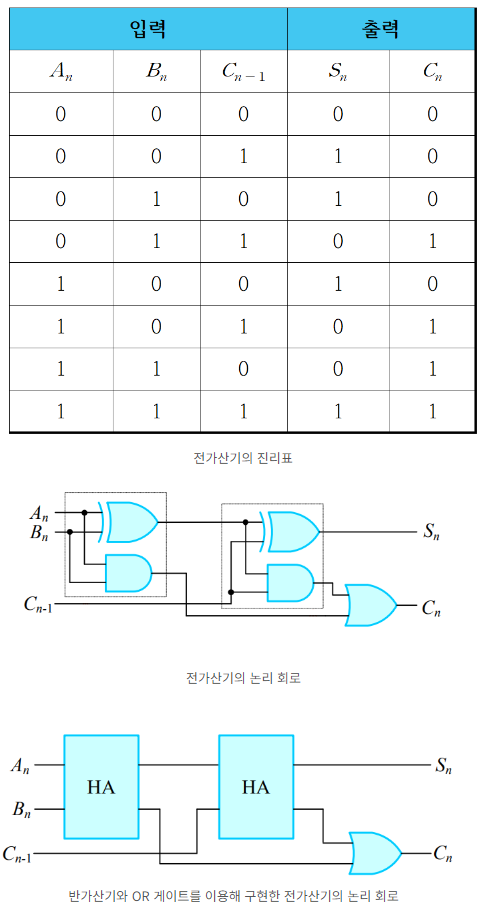
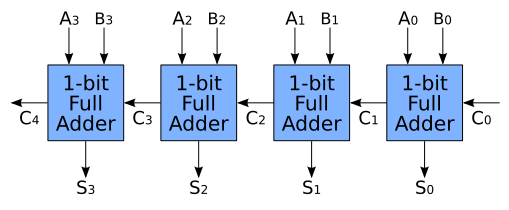
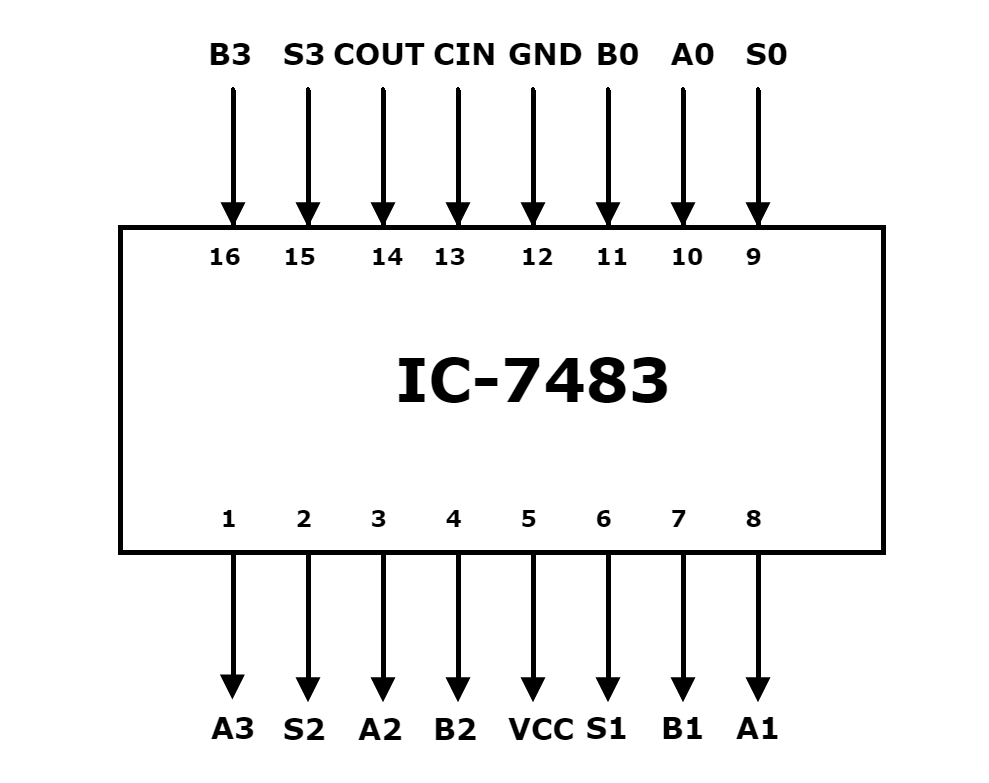
4비트 전가산기
전가산기를 연결하면, 여러 비트의 2진수를 한 번에 더하는 가산기를 구성할 수 있다.
PSpice
XOR
회로
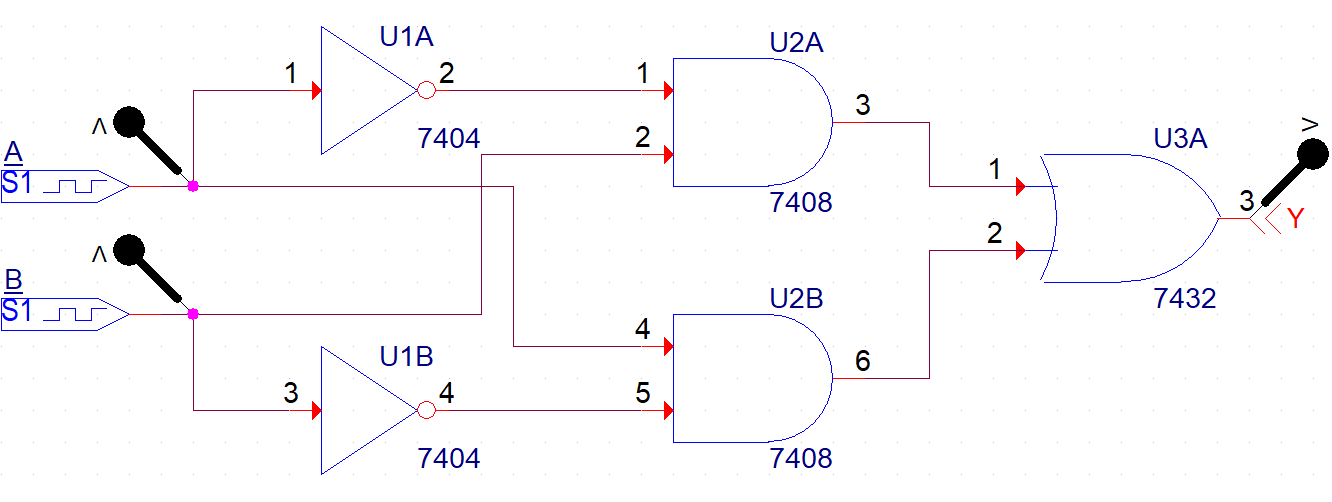
결과
XNOR
회로
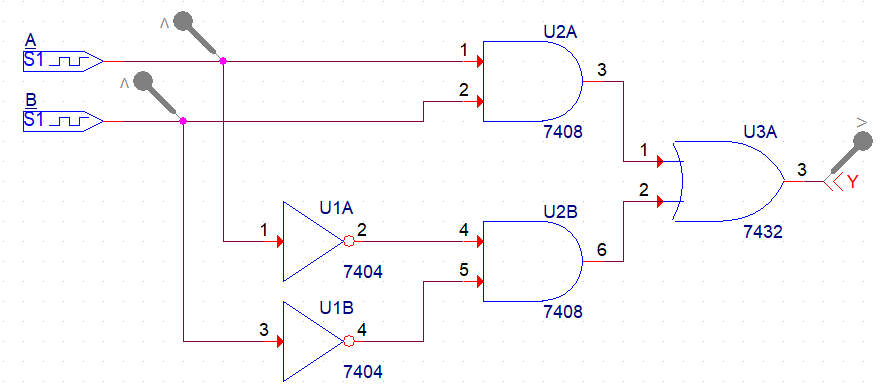
결과
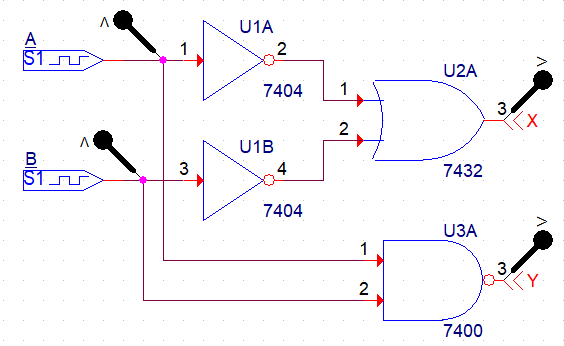
드 모르강의 제1정리
회로
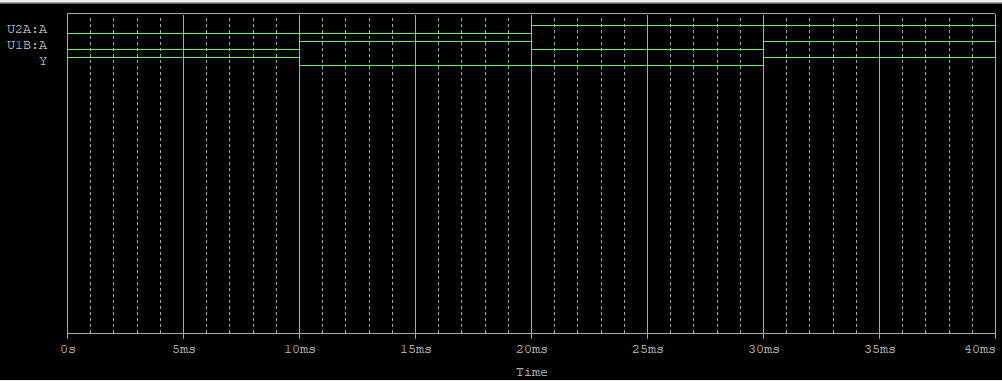
결과
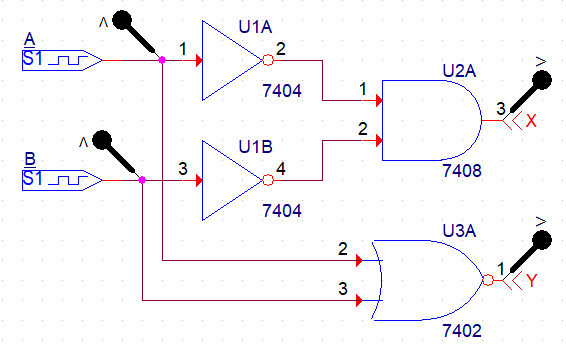
드 모르강의 제2정리
회로
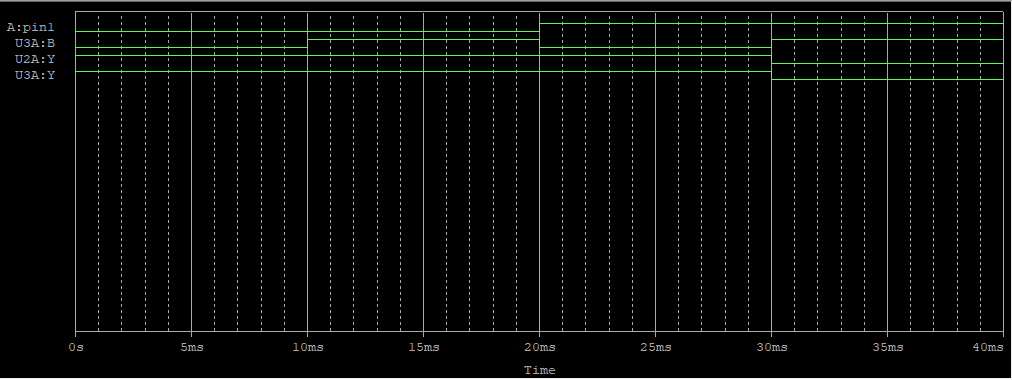
결과
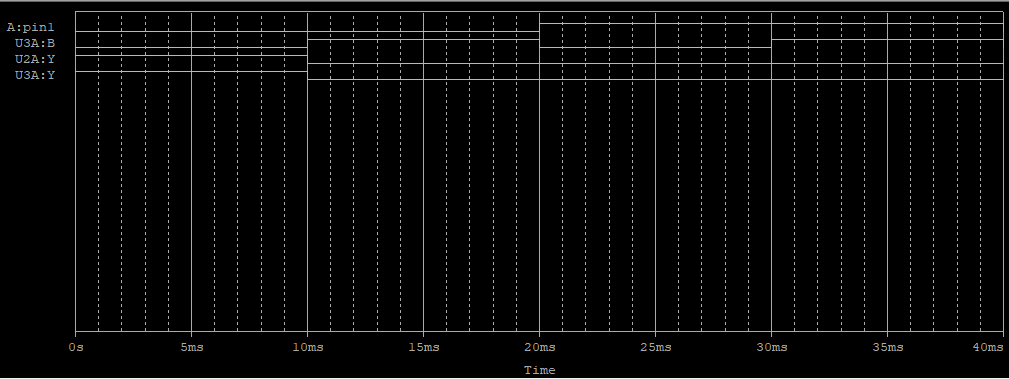
전가산기
회로
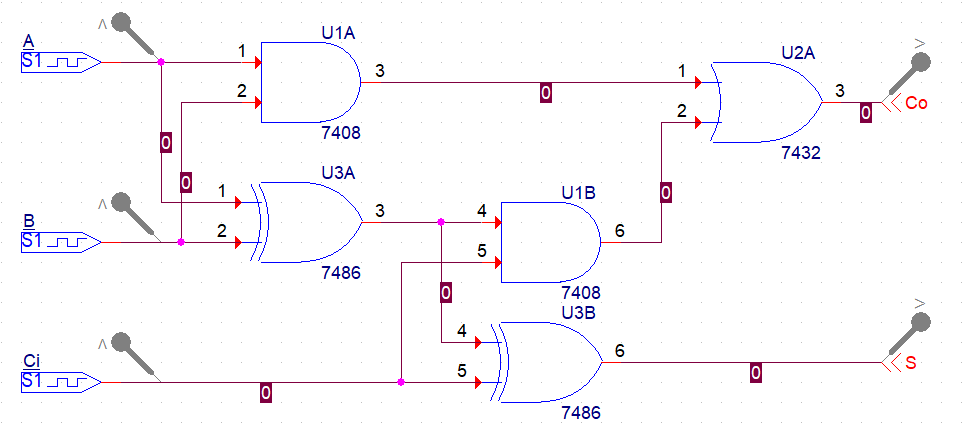
결과
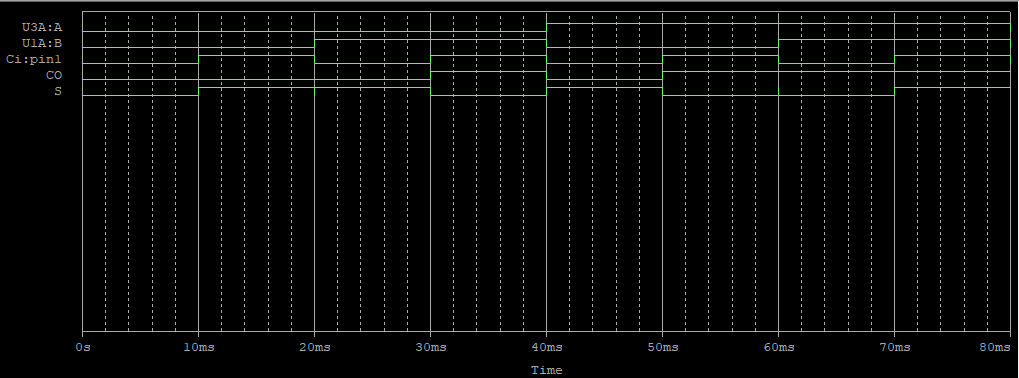
전감산기
회로
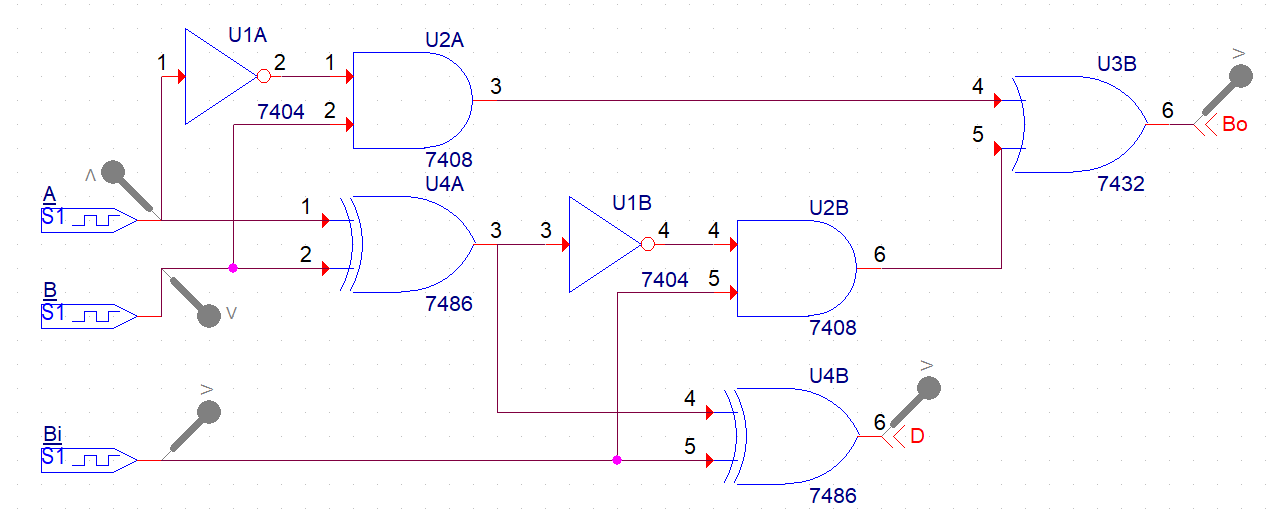
결과
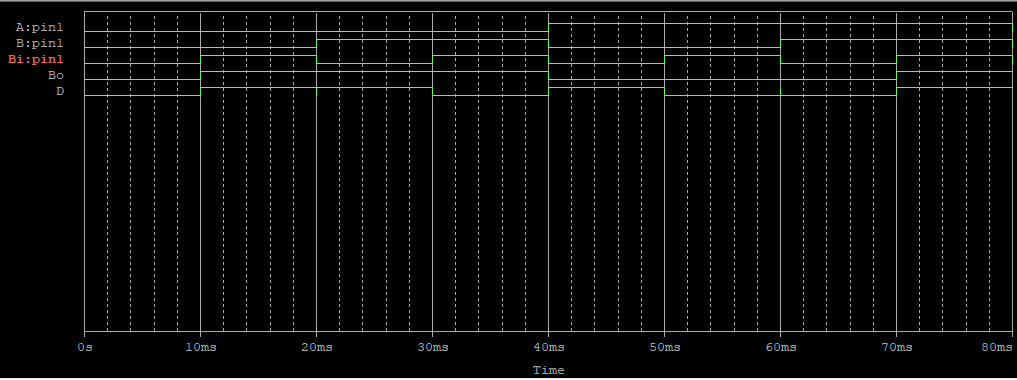
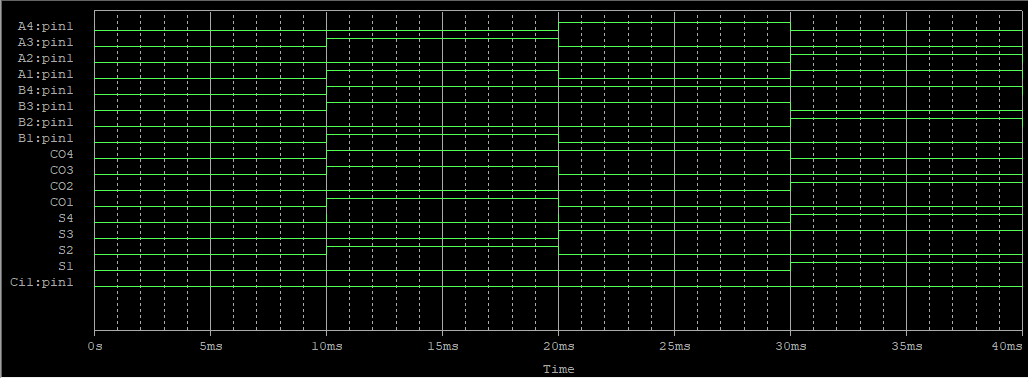
4비트 전가산기
| A4~A1 | B4~B1 | 4비트 합 | Co | Ci |
|---|---|---|---|---|
| 0101(5) | 0011(3) | 1000(8) | 0111 | 0 |
| 0111(7) | 1100(12) | 0011(3) | 0110 | 0 |
| 0110(6) | 0011(3) | 1001(9) | 0110 | 0 |
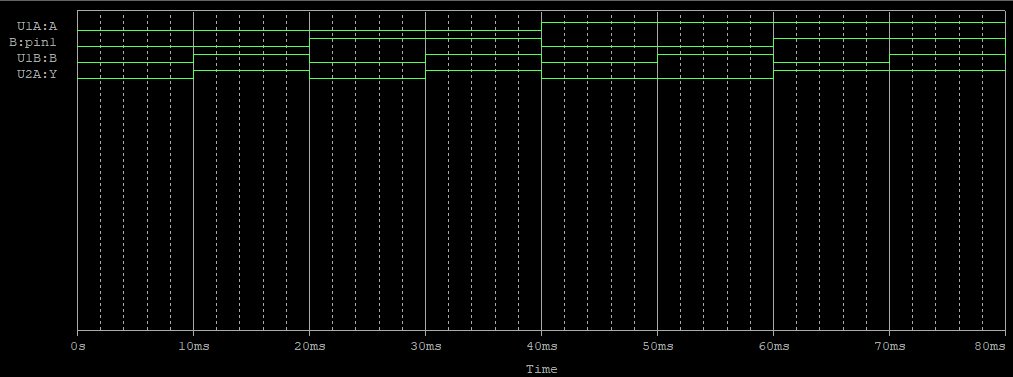
10ms간격으로 A의 첫 번째 비트 입력 110, 두 번째 비트 011, 세 번째 비트 111, 네 번째 비트 000, B도 마찬가지
회로
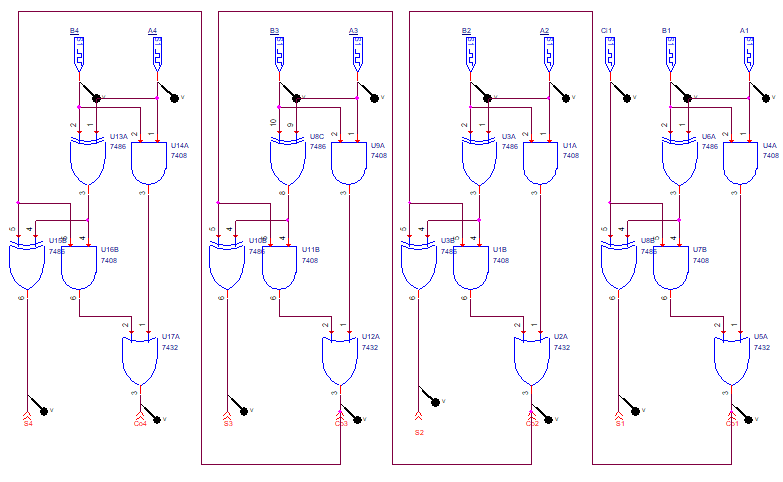
결과
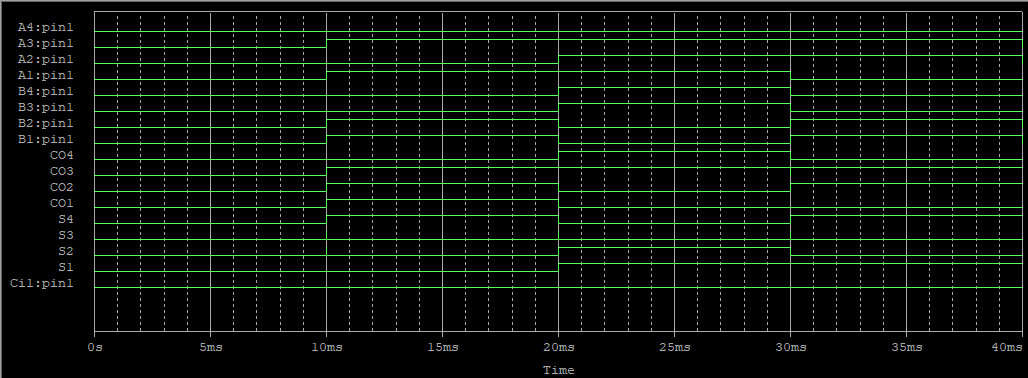
2의 보수를 이용한 감산
| A4~A1 | B4~B1 | 2의 보수 | 4비트 합 | Co | 감산 값 |
|---|---|---|---|---|---|
| 0101(5) | 0011(3) | 1101 | 1 0010 | 1101 | 0010(2) |
| 1000(8) | 0110(4) | 1100 | 1 0100 | 1000 | 0100(4) |
| 0011(3) | 0110(6) | 1010 | 0 1101 | 0100 | 1101(-3) |
결과