데이터베이스 이상현상(anomalies)
데이터베이스 이상현상이란 데이터베이스 설계가 잘못되었거나, 비정규화된 상태에서 발생하는 비효율적이고 부정확한 데이터 처리 문제를 의미한다.
아래 테이블로 삽입이상, 갱신이상, 삭제이상의 예시를 들어보자.
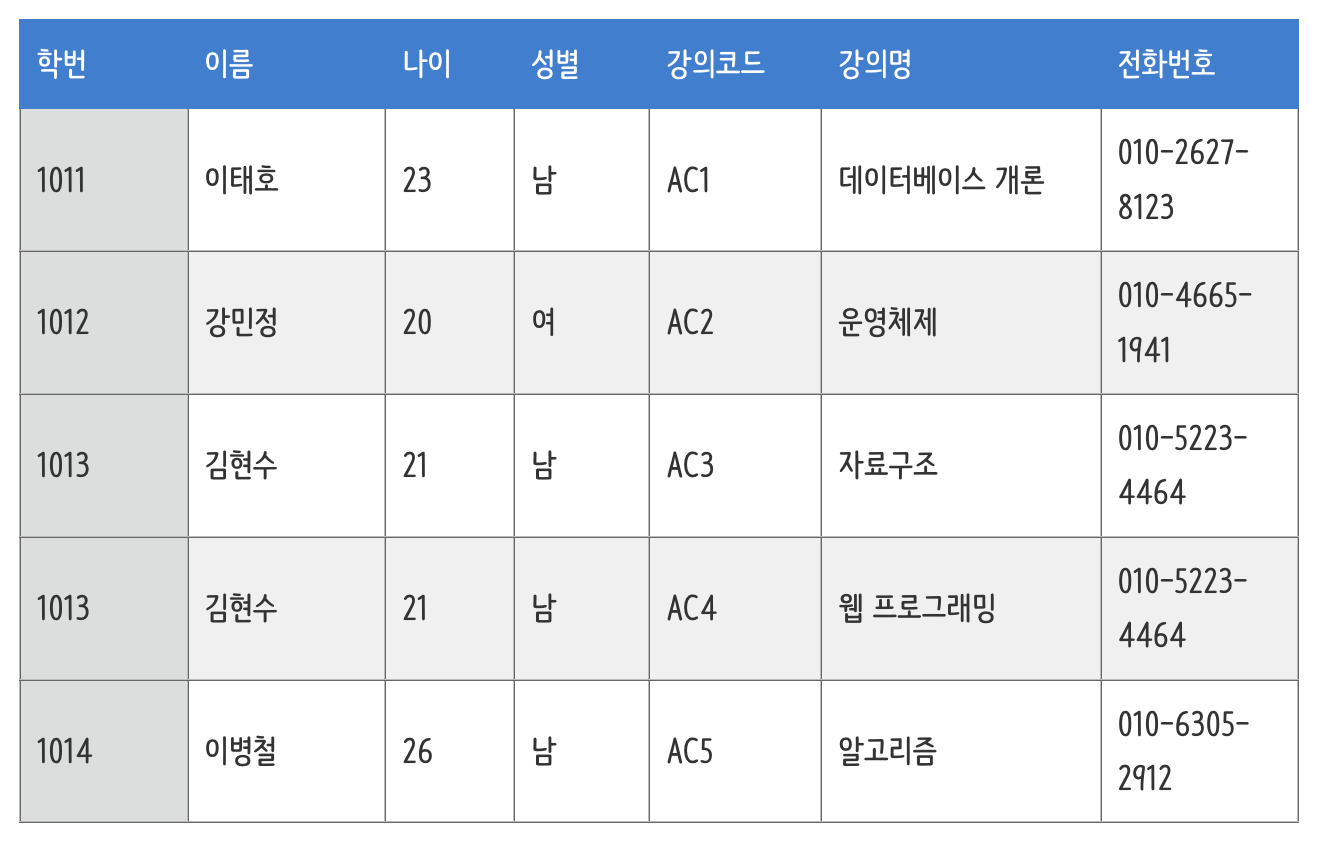
사진출처 - https://dev-coco.tistory.com/63
삽입이상
-
데이터 삽입 시 불필요한 데이터도 함께 삽입해야하는 문제
-
'컴퓨터 네트워크' 라는 새로운 강의가 추가되었을 때, 아직 수강하는 학생이 없을 수 있다. 그럼에도 데이터를 추가하기 위해서는 불필요한 학생 정보를 함께 삽입해야 한다.
갱신이상
-
데이터 중복으로 인해 일부만 수정하면 불일치가 발생하는 문제
-
'김현수' 학생의 전화번호를 수정했을 때, 중복된 모든 열을 찾아서 수정하지 않으면 불일치가 발생한다.
삭제이상
-
특정 데이터 삭제 시, 다른 연관된 데이터도 삭제되는 문제
-
'이병철' 학생의 정보를 삭제했더니, '알고리즘' 강의의 정보도 함께 삭제된다.
함수적 종속성(Functional Dependency)
함수적 종속성이란 특정 속성 집합(attribute)이 다른 속성 집합을 유일하게 결정 짓는 관계를 의미한다.
예를 들어, Primary Key는 테이블의 모든 속성을 유일하게 결정 지으므로
{PK} -> {All Attributes} 의 FD가 성립한다.
함수적 종속성은 개념적인 Schema로 판명해야한다. 특정 순간의 Instance로 판단하면 안된다.
즉, 함수적 종속성은 데이터 간의 본질적인 관계를 나타내며, 특정 순간의 데이터 상태가 아니라 데이터 스키마 설계를 기준으로 평가해야 한다.
1) 완전 함수적 종속성(Full Functional Dependency)
완전 함수적 종속성이란 어떤 속성들이 PK 전체에 의존하는 것을 의미한다.
PK의 일부만으로 결정되지 않고, 반드시 전체에 의존해야한다.

{학번, 강의코드}는 테이블에서 각 행을 고유하게 식별할 수 있는 최소 속성 집합이다.
{학번, 강의코드}->{이름}{학번, 강의코드}->{나이}{학번, 강의코드}->{성별}{학번, 강의코드}->{강의명}{학번, 강의코드}->{전화번호}
위와 같이 테이블의 모든 속성에 대해 함수적 종속성이 존재한다.
하지만, 이는 완전 함수적 종속성을 만족하지 않는다.
{학번}->{이름, 나이, 성별, 전화번호}{강의코드}->{강의명}
위와 같이 PK의 일부 속성 만으로 특정 속성을 결정 지을 수 있기 때문이다.
만약 테이블이 {학번, 이름, 나이, 성별, 전화번호} 만으로 구성되어 있고, PK가 {학번} 이라면, 완전 함수적 종속성을 만족할 것이다.
2) 부분 함수적 종속성(Partial Functional Dependency)
부분 함수적 종속이란, 기본키의 일부 속성만으로 특정 속성을 결정할 수 있을 때 발생한다.
위의 예시처럼 PK는 {학번, 강의코드} 인데, {학번} 만으로 결정지을 수 있는 속성들이 존재하는 상황이다.
3) 이행적 함수적 종속성(Transitive Functional Dependency)
이행적 함수적 종속성이란,
{A}->{B}{B}->{C}
의 FD가 존재할 때,
{A}->{C}의 함수적 종속성이 발생하는 상황을 의미한다.
이러한 현상은 주로 PK에 포함되지 않은 일반 속성이 또 다른 일반 속성을 결정 지을 때 발생한다. (PK -> {A} -> {B})
위의 예시를 다시 살펴보면, {전화번호} -> {이름} 으로의 FD가 존재한다.
{학번, 강의코드}->{전화번호}->{이름}의 이행적 함수 종속이 존재하는 것이다.
데이터베이스 정규화(Normalization)
데이터베이스 정규화란 Good Form(정규형)을 정하고, 모든 테이블이 Good Form이 될 때까지 Lossless Decomposition(무손실 분해)을 반복적으로 수행하는 것을 의미한다.
Lossless Decomposition(무손실 분해)란, 분해된 테이블을 다시 조인했을 때, 데이터 손실이 없는 것을 의미한다.
무손실 분해의 조건
Relation R을 R1과 R2로 분해할 때, 아래 둘 중 하나의 조건을 만족해야한다.
- {R1 ∩ R2} -> R1
- {R1 ∩ R2} -> R2
이를 통해 불필요한 데이터의 중복을 줄이며, 이상현상을 방지할 수 있다.
제 1 정규형
- 컬럼이 원자값(Atomic Value, 하나의 값)을 갖도록 테이블을 분해하는 것이다.
제 2 정규형
- 제 1 정규형을 만족한 테이블에 대해 완전 함수 종속을 만족시킨다. 즉, 부분적 함수 종속을 제거한다.
제 3 정규형
- 제 2 정규형을 만족한 테이블에 대해 이행적 함수 종속을 제거한다.
즉, 기본키를 제외한 속성들 간의 함수적 종속성이 존재하면 안된다.
BCNF 정규형
- 제 3 정규형을 만족한 테이블에 대해 모든 결정자가 후보키 집합에 속해야 한다.
- 즉, 후보키 집합에 속하지 않은 일반 속성이 결정자가 되면 안된다.
