기본 개념
- Sorting할 파일을 몇 개의 그룹(run)으로 분할
-> Run : 기억장치에 적재 가능할 크기의 여러 부분으로 분할된 각각의 작은 부분을 지칭함. - 각 run에 대해 내부 정렬 후 다른 파일에 저장
- 파일에 저장된 run들을 병합하여 다시 파일에 저장
- 병합된 run의 수가 1이 될 때까지 병합 반복
즉, 외부 정렬은 분할, 정렬, 병합 총 3단계로 구성되어 있음!
<병합 방법에 따른 sort/merge Algorithm의 분류>
- Binary Sort/Merge
- Balanced Binary Sort/Merge
- Balanced K-way Sort/Merge
- Polyphase Sort/Merge
Balanced : 입력과 출력의 파일 개수 같은 것
🤔 Binary Sort/Merge
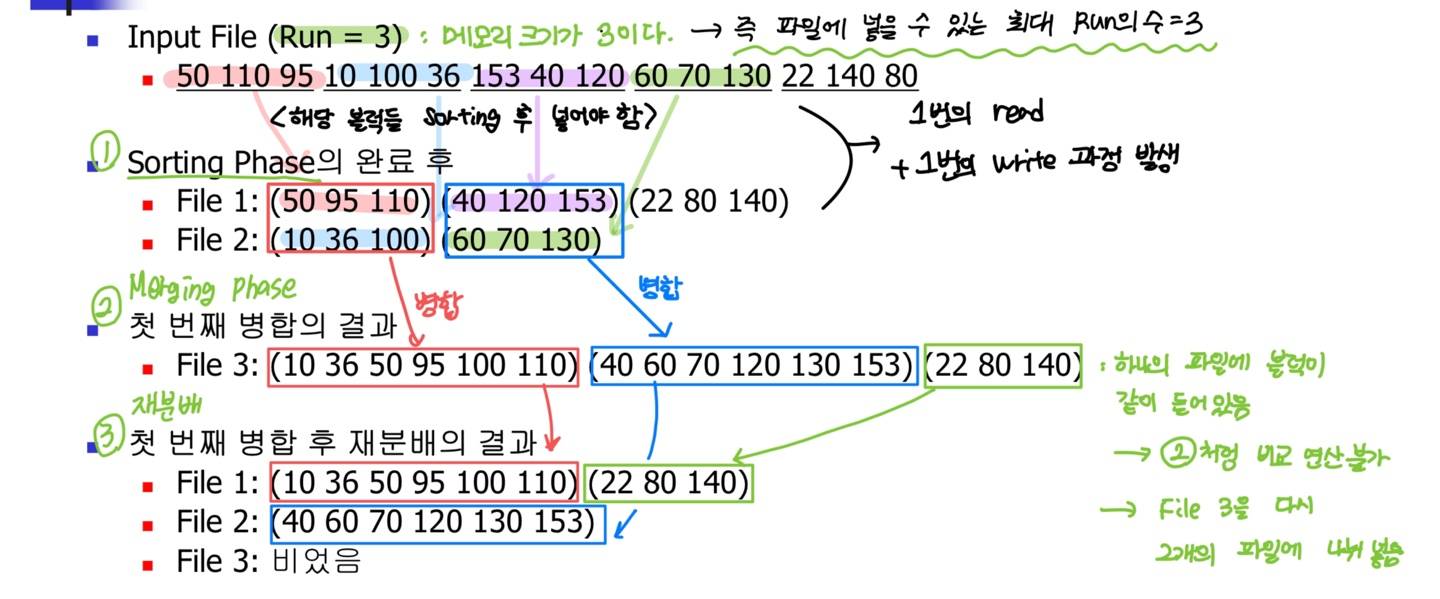
1. Sorting Phase
: 초기 run들을 sorting 한 후, 2개의 외부 파일에 저장
2. Merging Phase
: 각 파일에서 하나씩 run을 선택하여 큰 run으로 병합하여 해당 결과 파일 모두 세 번째 파일에 저장
: 하나의 파일 안에 모아진 결과 파일들을 다시 2개의 파일로 분배한 후 병합 진행
3. 재분배 과정
: 2개의 run이 병합되어 하나의 run에 들어가 있음
=> 또 다른 run과 다시 비교연산을 해주기 위하여 다시 파일 2개에 나누어 넣는 과정
⭐ 여기서 조건 : 파일은 Sequential File이다! (Random access File이 아니다.)
sequential File : 데이터가 순차적으로 저장되고 처리되는 방식
Random Access File : 파일 내의 특정 위치로 바로 접근하여 데이터를 읽고 쓸 수 있는 방식
3. 예시

해당 과정에서
- Sorting Phase : 1 read + 1 write
- Merginng Phanse : 1 read + 1 write
- 재분배 과정 : 1 read + 1 write
: 병합 과정은 이진 병합을 사용함. (= 각 병합 단계에서 run의 수를 반으로 줄일 수 있음 )
=> 즉, N개의 초기 run이 있다면, 이를 하나의 정렬된 파일로 병합하기 위한 단계의 수는 log₂N
( ex ) 초기 run이 8 개면, 파일은 8 -> 4 -> 2 -> 1 가 됨. 총 단계는 3개! )이 될 것
각 병합 단계에선 1번의 read와 1 번의 write가 발생하게 됨
- "병합 단계 수 " 시간 복잡도 : O(2log₂N)
- "Level 수 " : O(2log₂N) + 1 (맨 처음 Sorting phase를 +1로 취급)
최종 "병합 단계 수 " 시간 복잡도 : log₂N
"Level 수 " : log₂N + 1
N : run의 개수 의미 (!=크기)
🤔 Balanced Binary Sort/Merge
: Binary Sort에서 "재분배" 과정을 없앤 버전!
=> Binary Sort에서 성능이 상향된 버전이다.
Balanced : 입력과 출력 파일의 개수가 동일하다! (Binary니까 당연히 개수는 2개)
-> 실제로 BinarySort는 2개의 파일을 입력받아 1개의 출력파일 반환. 그 후 재분배를 통해 다시 2개의 입력파일로 나눈 후 다시 위의 과정 진행의 순서로 이루어지기에 비효율적!
1. Sorting Phase
: 초기 run들을 sorting 한 후, 2개의 외부 파일에 저장
2. Merging Phase
: 각 파일에서 하나씩 run을 선택하여 큰 run으로 병합 후, 각 결과를 다른 파일에 저장.
=> 각 파일을 다른 곳에 저장해줌으로써, 재분배 할 필요가 없어지게 됨!
=> 즉 "재분배" 과정이 삭제된 채 정렬이 가능해짐

Binary Sort/Merge 에서 재분배 과정만 제거되었기에, 병합 단계 수를 구하는 시간복잡도는 동일함
최종 "병합 단계 수 " 시간 복잡도 : log₂N
그러나, N이 커질 수록 성능이 떨어진다는 문제점이 발생함
=> Balanced K-way Sort/Merge 가 등장!
🤔Balaced K-way Sort/Merge
: 이전의 (balanced) binarySort/Merge에서의 시간복잡도는 N이 증가할수록 성능이 떨어지게 된다는 단점이 있었음. 해당 알고리즘은 이에 대한 보안책으로써 나옴!

이전과 달리 N에서 시작하여 K만큼 나누면서 1로 가는 계단의 수를 찾고 있음.
즉, 해당 알고리즘의 병합 단계 수 는 logₖN
최종 "병합 단계 수 " 시간 복잡도 : logₖN
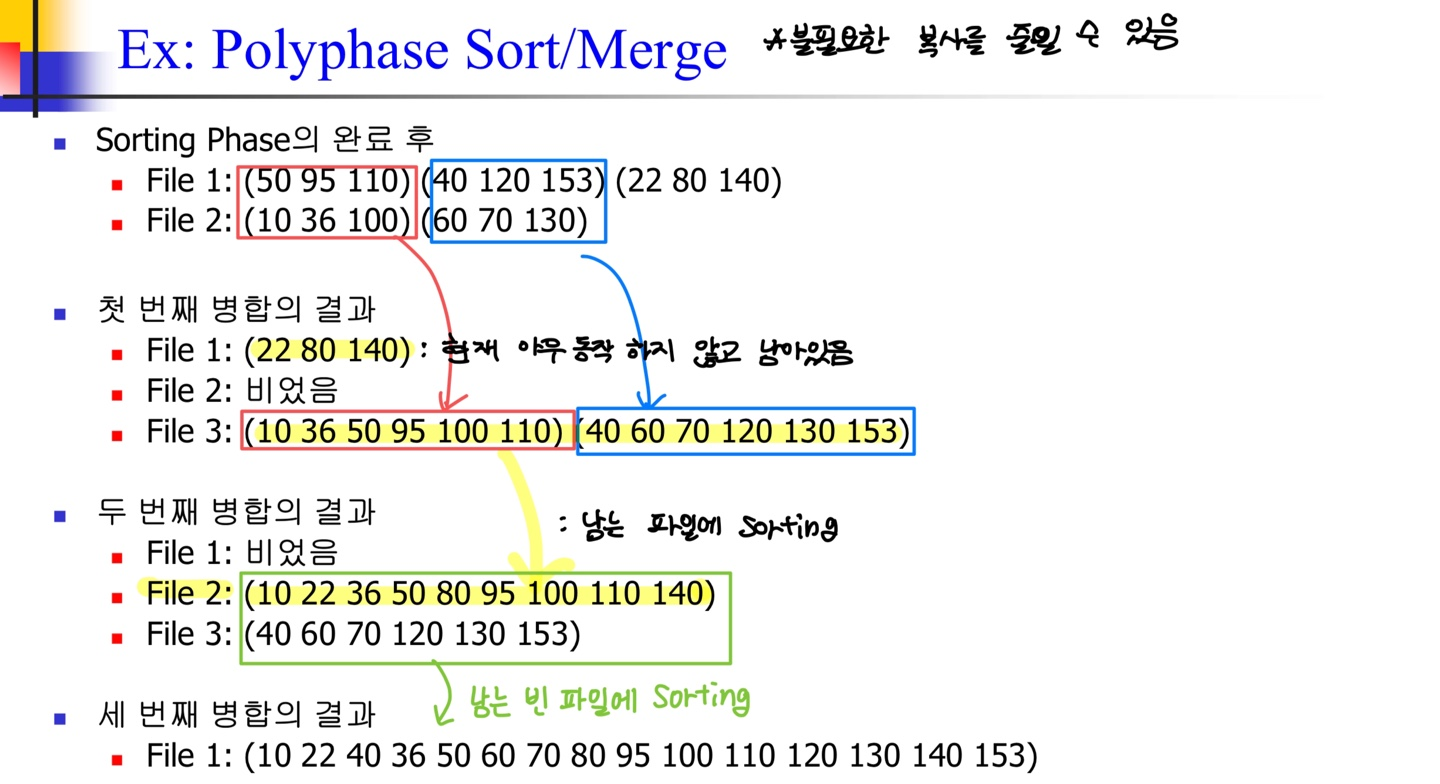
🤔PolyPhase Sort/Merge
: 이전의 방식에서 정렬되지 않은 run은 그냥 복사가 되었는데, 이런 불필요한 복사연산을 줄일 수 있는 방법!