특성값 및 특성 벡터의 이해

어떤 행렬 A와 벡터 v가 있다고 생각해보자. 행렬 A와 벡터 v의 곱과 v에 스칼라 곱을 했을 때 같아지게 하는 스칼라의 값을 특성값이라고 한다.

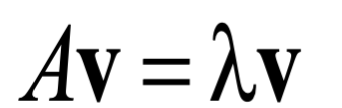
그림으로 이해하면 다음과 같다.

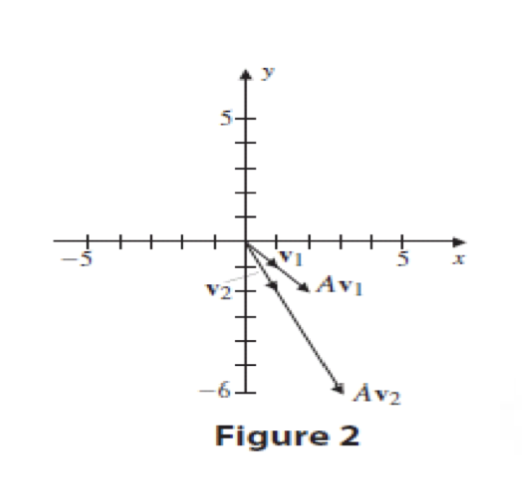
여기서 A와 벡터 v는 다음과 같다.

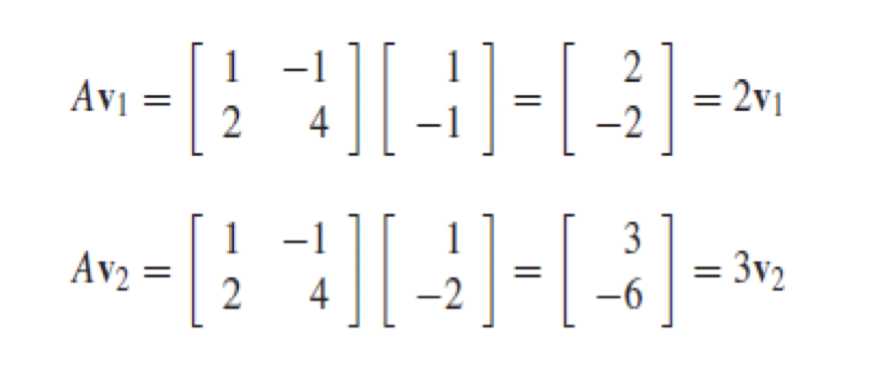
이때 특성 값을 체계적으로 구하기 위해 판별식을 사용한다.

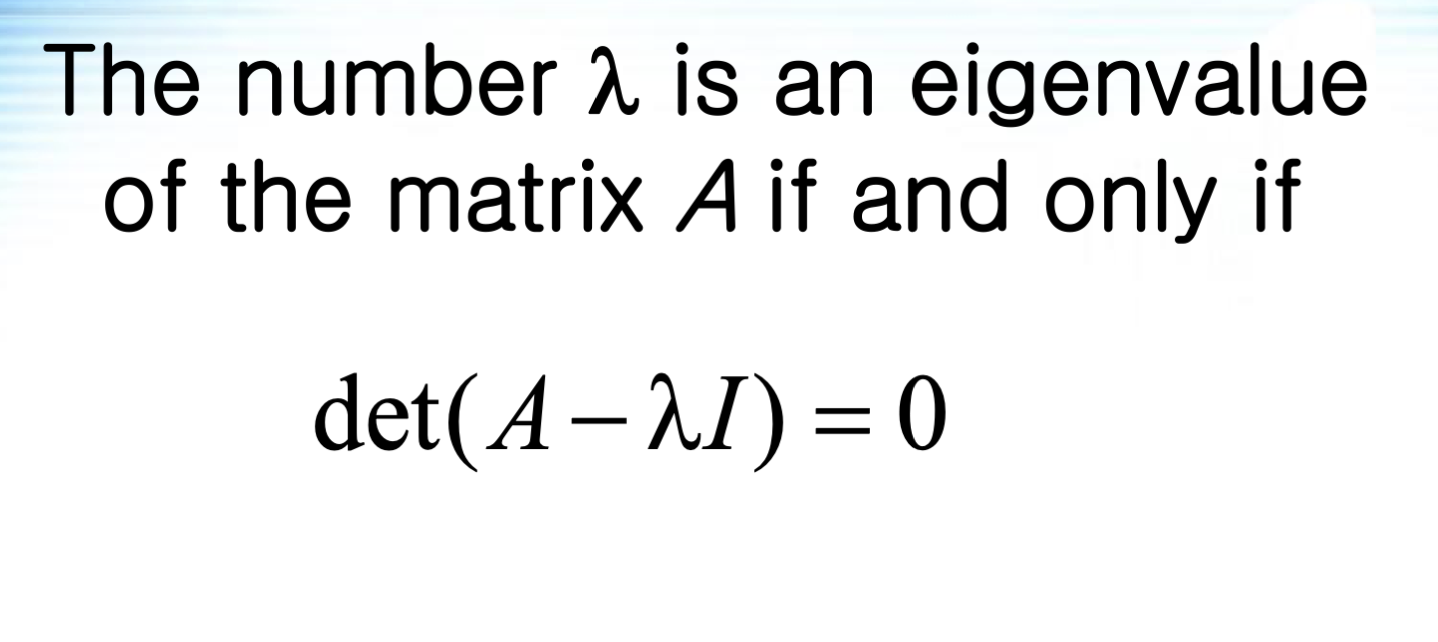
위 식을 통해 특성 값을 구하면 이제 특성 벡터를 구할 차례이다. 특성 벡터는 다음과 같다.

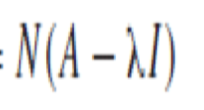
다음을 만족하는 공간을 구성하는 것이 특성 벡터이다. 따라서 특성 벡터는 어떤 공간으로 나온다. 예를 들어 이런식으로 나온다.

다음과 같이 어떤 특성 값에 대해 0공간을 만족하는 공간이 특성 벡터이다.