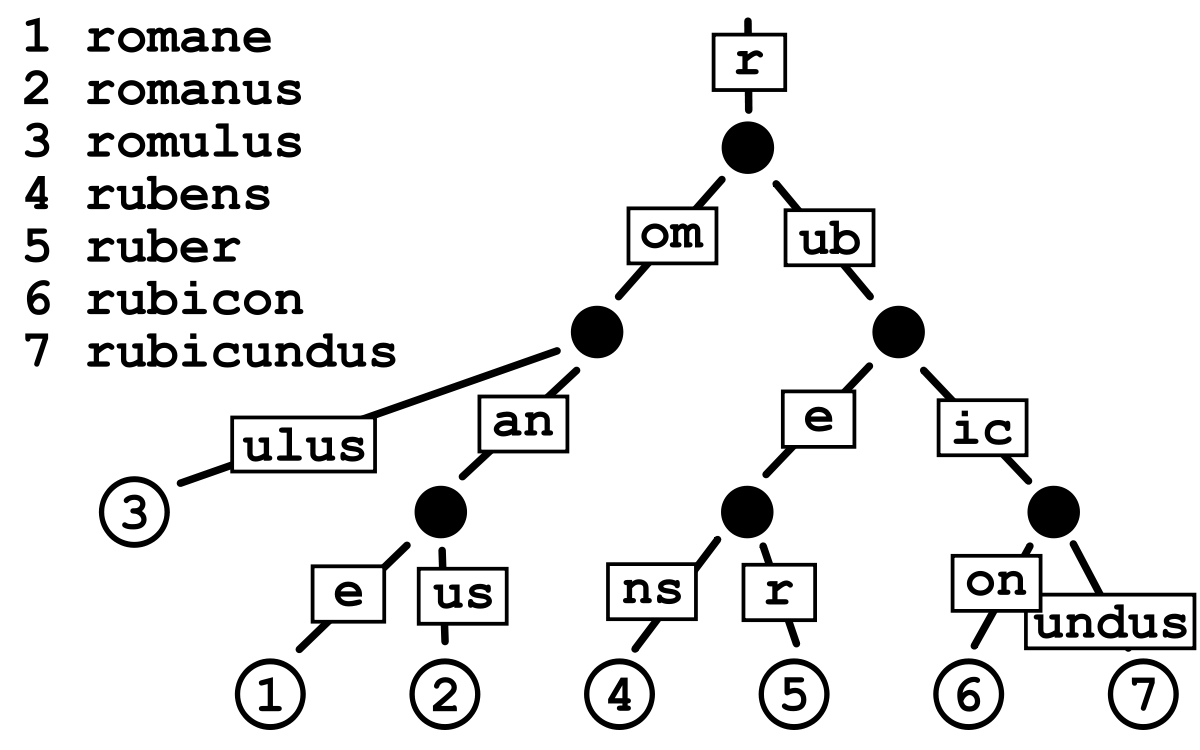
리트코드에서 위의 문제를 풀다가 Trie 자료구조에 대해 알게 되었다.
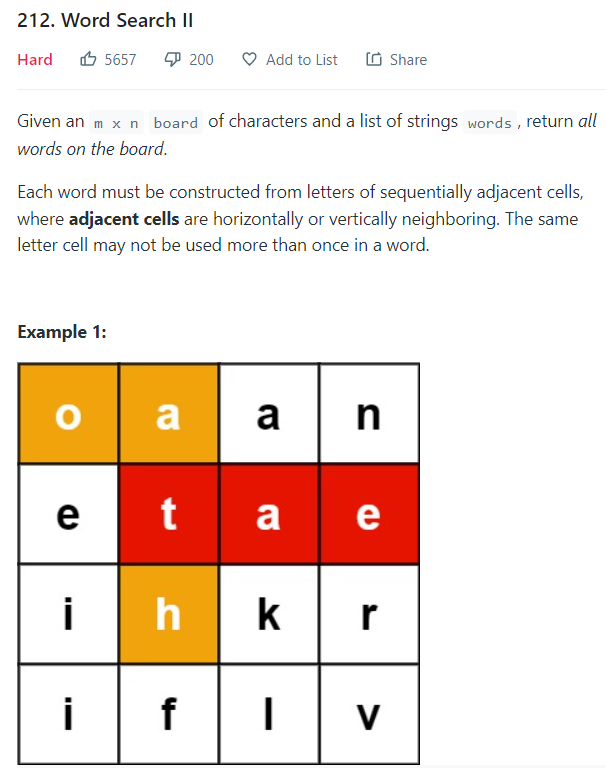
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]위의 212번 문제는 주어진 표 들에서 표와 단어들을 주면 해당 표에 주어진 단어들이 있는지 탐색하는 문제다.
dfs로 단어들이 각각 있는지 찾게 되었는데 코드를 작성하면서도 직감할 수 있었다. 시간초과가 날 것이라는 것. 더 효율적으로 풀 방법이 있다는 것을.. 그렇지 않고서야 이게 난이도가 HARD라는 것을.
역시나 결과적으로 시간초과가 발생하였고 Trie 자료구조를 사용하면 이를 개선할 수 있다.
찾아야하는 각 단어별로 매번 board에서 탐색을 하게 되니 시간초과가 발생하였는데 찾을 단어들을 Trie 자료구조로 미리 구성해 둔 다음 board는 단어의 수만큼 탐색했던 것과는 달리 한 번만 탐색하면서 Trie 자료구조에 넣어둔 단어와 일치되는 것이 있는지만 찾아볼 수 있다.
위 문제와는 별개로 Trie 자료구조에서 시간복잡도는 (m) m: 단어의 길이가 된다.
Trie 가 아닌 Binary Search tree로 해당 단어들을 저장해두었을 경우 시간복잡도는 m(단어의 길이) * log n(다음 문자를 탐색). 따라서 Trie 자료구조는 시간복잡도에서 강점을 갖고 있다.
공간복잡도는 어떻게 될까?
단어들이 중복되는 부분이 없다면 다른 BST와 마찬가지로 공간복잡도는 각 단어들 길이의 합 만큼 생성되겠지만, 단어들 중 첫 시작부터 중복되는 부분은 별개로 저장되는 것이 아닌 트리 구조로 중복시킨다. 'apple' , 'applepie' 의 단어를 예로들자면 'applepie' 를 저장하고 중간과 마지막의 'e'를 단어의 끝이라는 점을 마킹해둠으로서 두 단어를 별개로 저장하지 않는다.
그림) 'apple' 'applepie' 'banana' 'bananacake' 'cake' 'juice' 를 저장하는 경우
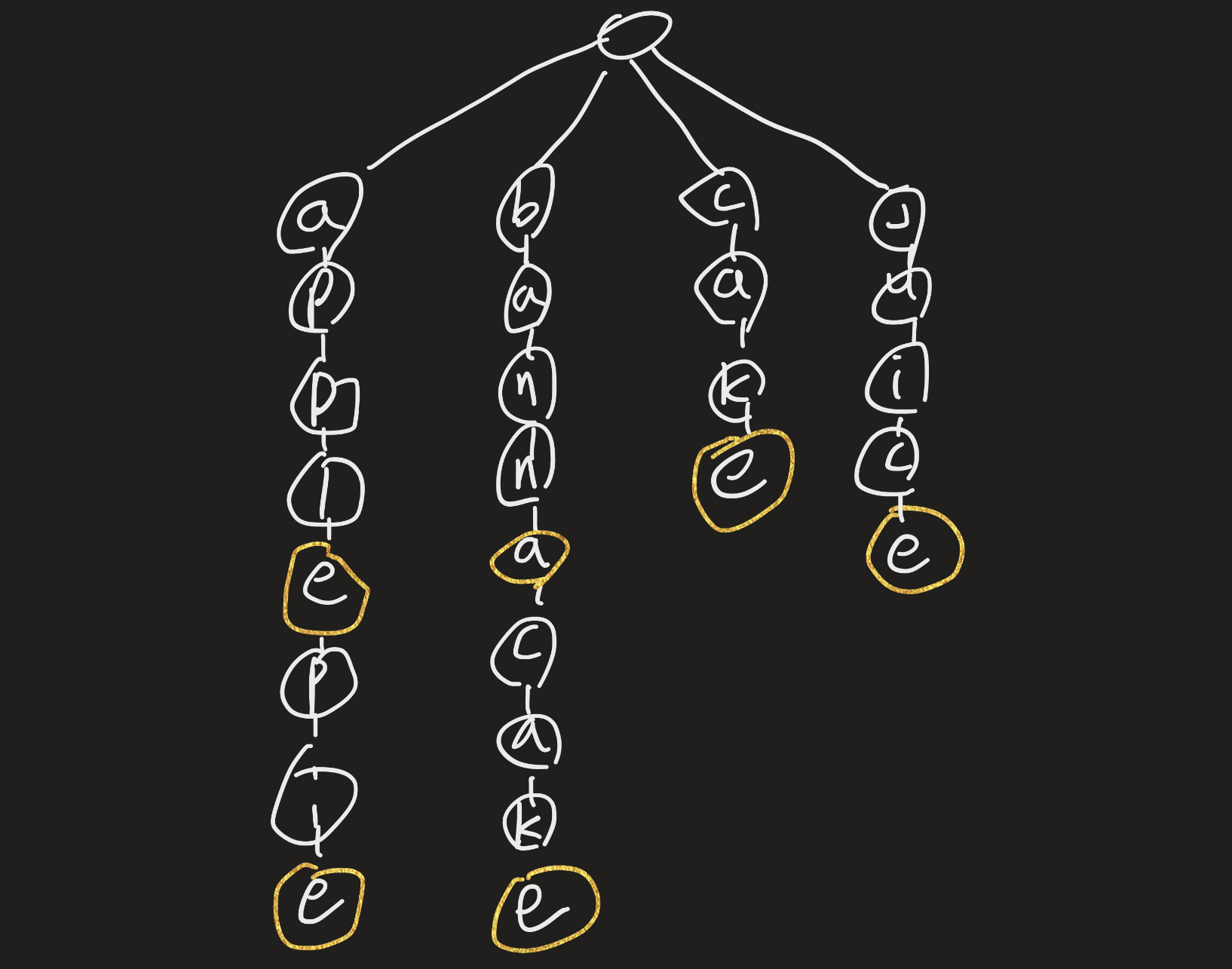
그럼 메모리 이용률도 좋은걸까? 메모리 이용률이 괜찮아보이지만 실제 사용하게 되었을 때 데이터가 많다면 각 노드에서 다음 노드를 가리키는 포인트가 굉장히 많이 생성된다. 알파벳의 경우 그 다음으로 가는 노드가 26개가 생성된다. 또한 각 노드에서 해쉬로 다음 노드로 연결하며 각 노드에서도 해당 노드가 end포인트를 체크가 필요하기에 시간복잡도는 좋지만 메모리를 많이 잡아먹게 된다.
Trie 자료구조 <- 이 문제는 Trie 자체를 구현하는 문제이다.
# Trie DataStructure
class TrieNode: # 각 노드
def __init__(self):
self.children = {} # 다음 노드로 이어짐
self.endOfWord = False # 단어의 마지막을 표시하기 위한 마킹. False는 마지막이 아님, True는 마지막
# 위 그림에서 노란색, 흰색을 결정하는 부분
class Trie:
def __init__(self): # 시작 Root 노드 생성
self.root = TrieNode()
def insert(self, word: str) -> None: # 단어를 추가하기
cur = self.root
for c in word: # 각 단어를 하나씩 넣으면서 중복된 것이 아니라면 새롭게 가지치기
if c not in cur.children:
cur.children[c] = TrieNode() # 가지치기
cur = cur.children[c]
cur.endOfWord = True # 마지막 단어의 경우 마지막이라고 마킹해줌
def search(self, word: str) -> bool: # 해당 단어가 있는지
cur = self.root
for c in word: # 단어를 하나씩 타고 내려감
if c not in cur.children:
return False # 하나라도 다른게 나오면 False를 Return
cur = cur.children[c]
return cur.endOfWord # 마지막이 해당 단어의 끝이여야 True 를 Return
def startsWith(self, prefix: str) -> bool: # 해당 prefix로 시작하는 단어가 있는지. 단어의 마지막이 끝지점인지를 확인할 필요가 없음.
cur = self.root
for c in prefix:
if c not in cur.children:
return False
cur = cur.children[c]
return True

참고
https://en.wikipedia.org/wiki/Trie
https://www.geeksforgeeks.org/trie-insert-and-search/
