선밸런싱 이후 삽입, 삭제하는 레드블랙트리

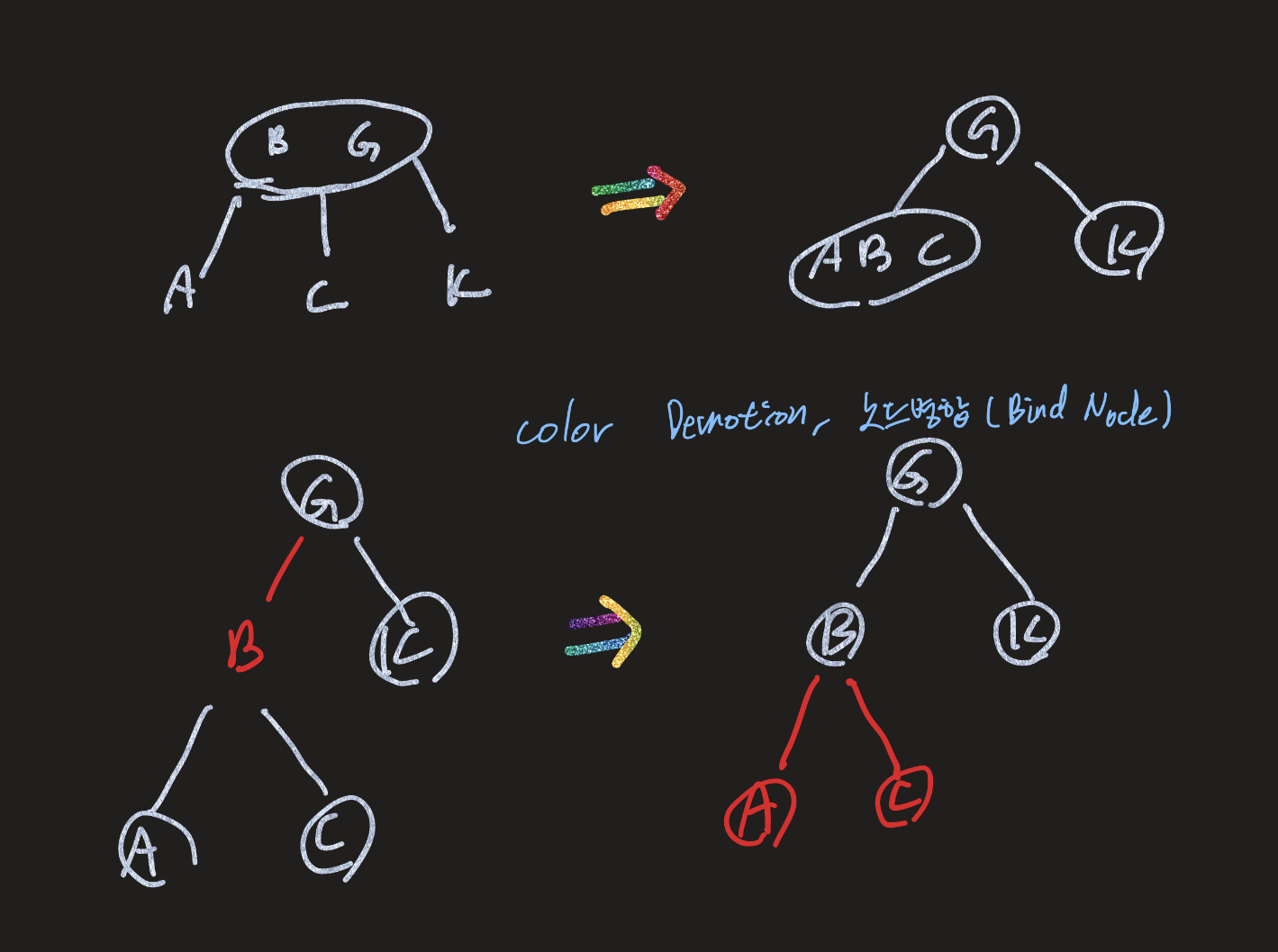
RB트리 - 시간복잡도

트리의 시간복잡도는 높이에 의해 결정되는데,
Binary Search Tree 의 경우 root 노드의 key 값을 기준으로 크거나, 작은 데이터만 일관적으로 삽입하게 되면 높이가 n으로 되면서 시간 복잡도 n 이 발생하게 된다. 트리 구조의 장점인 시간복잡도 log n의 장점을 살리지 못하는 것이다.

그리하여 노드에 비트 하나를 추가하여 red, black으로 노드의 색을 구분하고 밸런싱한 RB트리는 Log n의 시간복잡도를 보장한다.

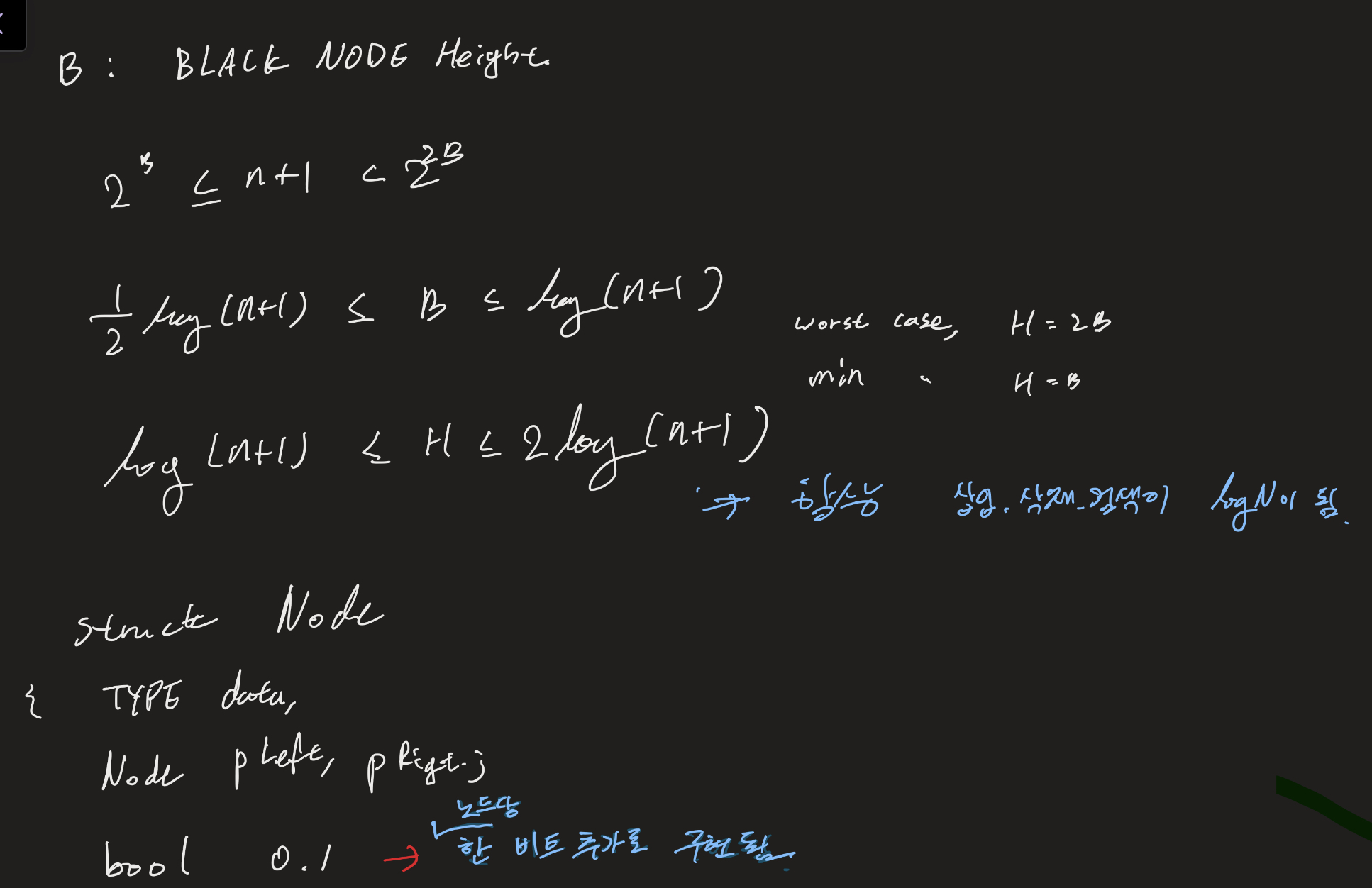
c언어로 레드블랙트리를 구현하게 되었는데,

어떤 것을 참고할지 여러 자료들을 찾아보던 도중.. 뭔가 엄청난걸 찾아내었다고 생각했다

모든 mit강의를 비롯하여 원서 등의 자료들이 삽입, 삭제의 선처리를 해준 이후 밸런스를 맞추기 위해 추가, 삭제된 데이터들을 기준으로 트리를 리밸런싱을 해주었는데, 선밸런싱을 해준 이후 삽입, 삭제하는 방법이 있는 것이었다..!

트리 구조에서 루트를 타고 내려가며 삽입, 삭제할 데이터를 찾아 내서 처리 한 이후, 다시 트리의 구조를 보며 밸런싱을 하는것이 어찌보면 당연해보이는데, 트리 루트에서부터 타고 내려가며 어디에 위치해있는지 모르는 상태에서 어떻게 밸런싱, 즉 트리구조를 움직여가며 내려갔다가 삽입 삭제를 해주는거지..? 이건 엄청나다..!! 라며 매료되었다.

그리하여 선밸런싱 이후 처리 방식과 선처리 이후 리밸런싱 두가지 방식의 장단점은 마지막에 기술하기로하고, 선밸런싱 레드블랙트리의 특징에 대해 알아보자.

RB트리의 성질

• 부모노드는 왼쪽 서브트리보다 크고 오른쪽 서브트리보다 작다. - BST와 동일
• Root 에서 Leaf로 가는 경로의 검정 노드의 수는 모두 같다.
• 새로 삽입되는 노드는 Leaf에 위치하며 빨간 노드이다.
• 경로상에 연이어 두 개의 빨간노드가 있을 수 없다. (회전필요)
• 부모의 두 자식노드가 모두 빨간 노드이면, 부모를 빨간 노드로 하고 자식은 검정 노드로 바뀔 수 있다.(색상변환)
• Root 노드는 빨간 노드일 수 없다.(검정으로 변환)
• 빨간 노드는 자식이 없던가, 있다면 두개의 검정 노드이다.
• 검정 노드는 자식이 없던가, 있다면 하나의 빨간 노드나, 두개의 빨간 노드나 두 개의 검정노드를 가진다. 즉, 하나의 검정 노드를 자식으로 가질 수 없다.

코드로 보는 RBTree

- insert

Delete를 할 경우에는 고려해줘야 할 상황들이 많은 것에 비해 Insert는 간단하다. 아래 그림에서 D를 삽입한다고 생각해보자.

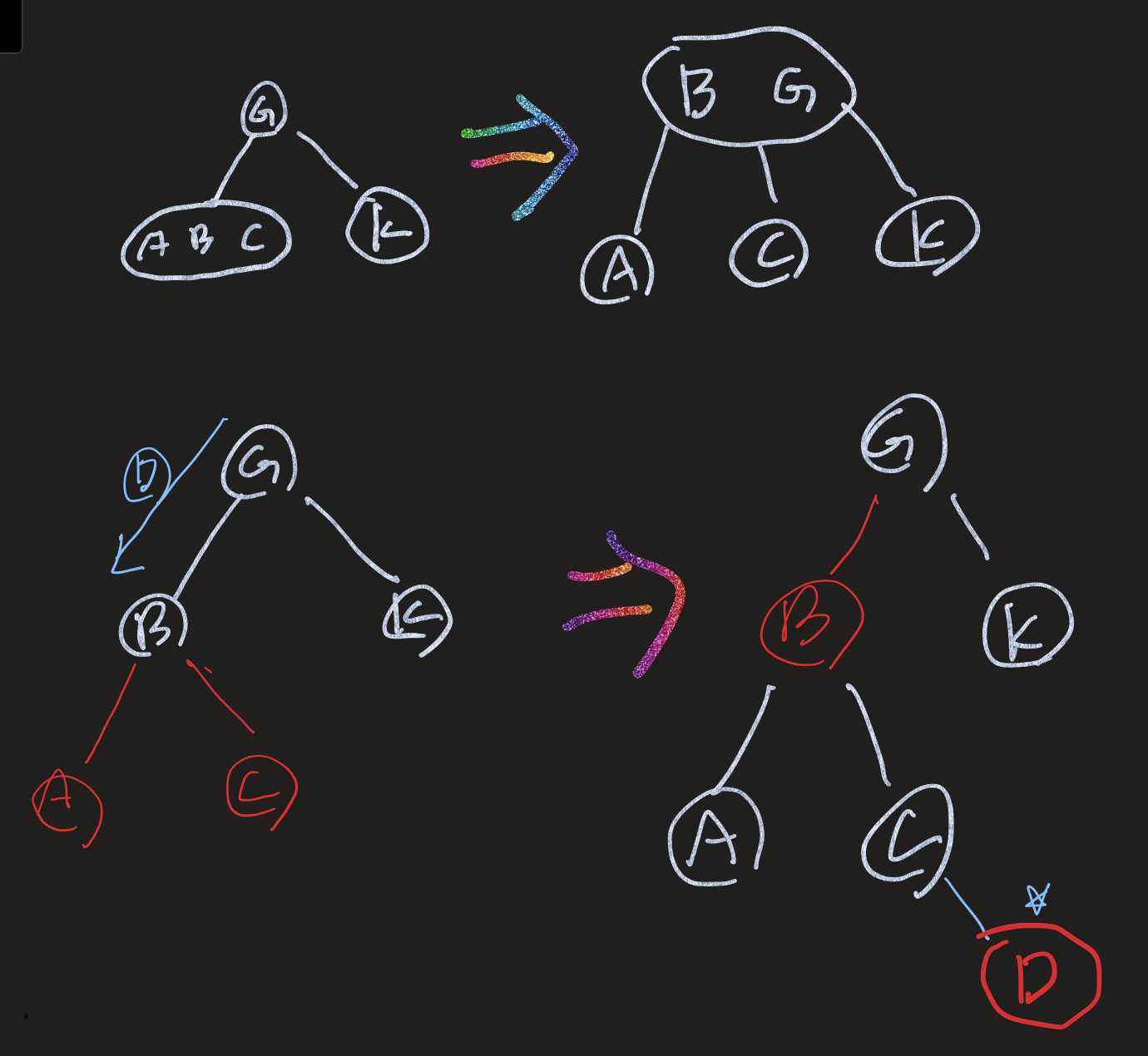
• 삽입하려고 트리를 내려가다가 아래 두 child 노드가 Red 노드일 경우 해당 노드의 색을 Black으로 바꾸고 그 parent node를 Black으로 바꿔준다. (상향 색변환 - Color Promotion, B-Tree의 Split(분할)과 같다고 한다.)

이 한 규칙으로 인해 파생되는 상황들이 발생하는데, 위 과정을 거칠 경우 RB 트리의 성질 중 RED node가 연달아 달리는 경우가 발생하는데, 그럼 Rotation의 과정을 통해 blance를 재조정 해 준다.

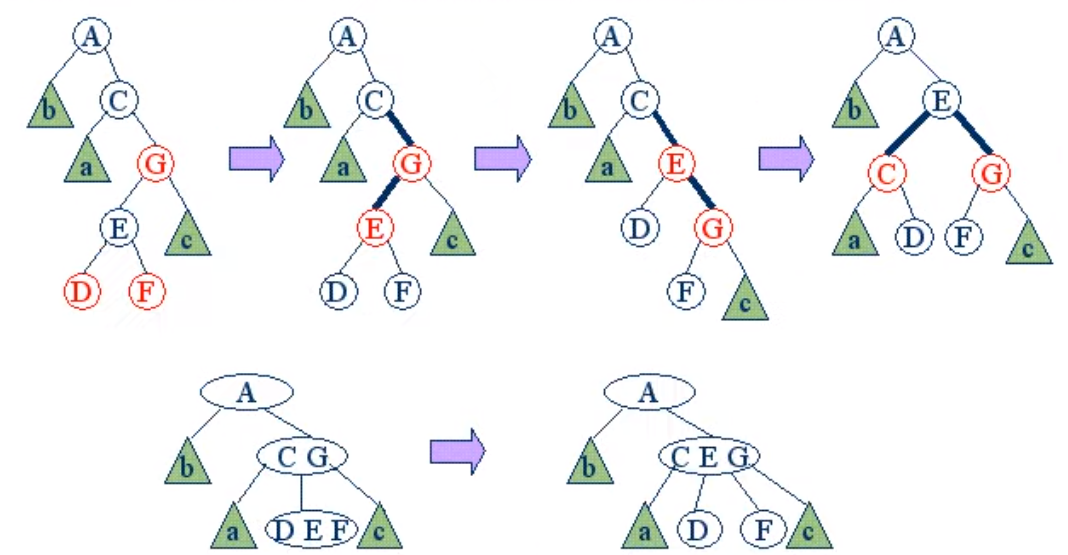
위 사진은 Right rotation을 한번 수행 해 준 후 left Rotation을 한번 다시 해주는 예시이다.

상황에 따라 Right-left, Left-right, Left, Right 로테이션을 해주고 insert를 하게 된다.

node_t *rbtree_insert(rbtree *t, const key_t key)
{
  if (t->root == NULL)
  {
    t->root = (node_t *)calloc(sizeof(node_t), 1);
    t->root->key = key;
    t->root->color = RBTREE_BLACK;
    t->root->left = t->root->right = NULL;

    // node_t *head_node;
    head = malloc(sizeof(node_t));
    head->left = t->root;
    head->color = RBTREE_BLACK;
    head->right = head->parent = NULL;

    return t->root;
  }

  node_t *curr, *p, *gp, *ggp;
  ggp = gp = p = (node_t *)head;
  curr = (node_t *)head->left;

  while (curr)
  {
    if (key == curr->key) // RB트리는 key값 중복을 허용하지 않음! 
    {
      head_node_to_t_root(t);
      return NULL; 
    }

    // 자식 노드 둘 다 있고 빨강이면 color promotion. 위에서 언급한 한 가지 규칙
    if (curr->left && curr->right && curr->left->color == RBTREE_RED && curr->right->color == RBTREE_RED)
    {
      curr->color = RBTREE_RED;
      curr->left->color = curr->right->color = RBTREE_BLACK;

      // 부모가 빨강이면 rotation. color Promotion을 해 준후 연달아 red node가 발생한 상황. rotation해줘야함
      if (p->color == RBTREE_RED)
      {
        gp->color = RBTREE_RED;
        if ((key > gp->key) != (key > p->key)) // 이 조건에 따라 두번의 rotate(right-left, left-right)가 발생할지,
          p = rotate(t, key, gp); 
        curr = rotate(t, key, ggp); // 아니면 단일 rotation이 발생할지 결정됨
        curr->color = RBTREE_BLACK;
      }

      // 뿌리는 항상 검정
      head->left->color = RBTREE_BLACK; // 여기 화살표 왜 빨강색이야 무섭게 ㄷㄷ
    }
    
    // 한 칸씩 내려가기
    ggp = gp;
    gp = p;
    p = curr;
    if (key > curr->key)
      curr = curr->right;
    else
      curr = curr->left;
  }
  curr = (node_t *)malloc(sizeof(node_t));
  curr->left = curr->right = NULL;
  curr->key = key;
  curr->color = RBTREE_RED;

  if (key > p->key && p != head)
    p->right = curr;
  else
    p->left = curr;

  // 다 내려와서 위치 찾고 red node로 insert를 했더니 부모가 빨강이면 마지막으로 회전!

  if (p->color == RBTREE_RED)
  {
    gp->color = RBTREE_RED;
    if ((key > gp->key) != (key > p->key))
      p = rotate(t, key, gp);
    curr = rotate(t, key, ggp);
    curr->color = RBTREE_BLACK;
  }

  // root는 항상 검정으로
  head->left->color = RBTREE_BLACK;

  head_node_to_t_root(t);
  return curr;
}

Delete

Delete의 경우도 삭제하러 내려가면서 parent node를 red로 유지하도록 한다. 이는 삭제하려는 data가 있는 쪽으로 삭제노드를 찾아내려가며 color Demotion 후에 삭제 후에도 밸런스를 유지하기 위한 방법이다.
insert에 비해 확인해줘야할 if문과 그에 파생되는 함수들이 insert에 비해 많은 편 이다.

int rbtree_erase(rbtree *t, node_t *p)
{
  node_t *delgp, *delp, *del, *sib;
  key_t value = p->key;
  delgp = delp = head;
  del = head->left;
  sib = 0; // sib = NULL??
  while (isLeafNode(del) == false) // 지우려는 노드가 리프노드가 될 때 까지 진행
  {
    if (del->color == RBTREE_BLACK) // parent node를 항상 red로 만들고 내려간다. if, 블랙일 경우
    {
      if (redAsParent(t, delgp, delp, sib) == true)
      {
        // delgp 와 sib의 위치가 변했다. 새로 수정
        delgp = sib;
        if (del->key > delp->key || del->key == delp->key)
          sib = delp->left;
        else
          sib = delp->right;
      }
    }
    if (del != head->left && is2Node(del) == true) // root 가 아니고 2노드이면 부풀려줘야함 
    {
      if (borrowKey(t, delgp, delp, del, sib) == false) // 부풀려주기 위해서 borrowKey를 하거나
        bindNode(delp);	// Borrow 키를 할 상황이 아니면 bindNode
    }

    if (value == del->key)
      value = swapKey(del);

    delgp = delp;
    delp = del;
    if (value > del->key || value == del->key)
    {
      // swapkey로 인해 같은 값이 나올 수 있음.
      // In-order successor를 사용하기 때문에 오른쪽으로
      sib = del->left;
      del = del->right;
    }
    else
    {
      sib = del->right;
      del = del->left;
    }
  }
  // while 문 종료
  if (del->color == RBTREE_BLACK)
  { // del 이 black 이면 rotation
    if (redAsParent(t, delgp, delp, sib))
    {
      // delgp 와 sib의 위치가 변했다. 새로 수정
      delgp = sib;
      if (del->key > delp->key || del->key == delp->key)
        sib = delp->left;
      else
        sib = delp->right;
    }
  }
  if (del != head->left && is2Node(del))
  {
    if (!borrowKey(t, delgp, delp, del, sib))
      bindNode(delp);
  }

  if (delLeafNode(t, value, delp, del))
  {
    head_node_to_t_root(t);
    return true;
  }
  else
  {
    head_node_to_t_root(t);
    return false;
  }
}

다음은 삭제 메인 로직에 사용되는 함수들이다

/* functions */
node_t *rotate(rbtree *t, const key_t key, node_t *pivot)
{
  node_t *child, *gchild;
  if ((key > pivot->key || key == pivot->key) && pivot != head)
    child = (node_t *)pivot->right;
  else
    child = (node_t *)pivot->left;

  if (key > child->key || key == child->key) //Rotate Left
  {
    gchild = (node_t *)child->right;
    child->right = gchild->left;
    gchild->left = (node_t *)child;
  }
  else
  {
    gchild = (node_t *)child->left;
    child->left = gchild->right;
    gchild->right = (node_t *)child;
  }
  if ((key > pivot->key || key == pivot->key) && pivot != head)
    pivot->right = gchild;
  else
    pivot->left = gchild;

  return gchild;
}

bool isLeafNode(const node_t *p)
{
  if (p == 0) // null ? 0 ??
    return false;
  if ((p->left == 0 || (p->left && p->left->color == RBTREE_RED && !p->left->left && !p->left->right)) &&
      (p->right == 0 || (p->right && p->right->color == RBTREE_RED && !p->right->left && !p->right->right)))
    return true;
  else
    return false;
}

bool is2Node(const node_t *p)
{
  if (p == 0)
    return false;
  if (p->color == RBTREE_RED)
    return false;
  if ((p->left == 0 && p->right == 0) || (p->left && p->right && p->left->color != RBTREE_RED && p->right->color != RBTREE_RED))
    return true;
  else
    return false;
}
bool redAsParent(rbtree *t, node_t *delgp, node_t *delp, node_t *sib)
{
  if (sib == 0 || sib->color != RBTREE_RED)
    return false;
  rotate(t, sib->key, delgp);
  sib->color = RBTREE_BLACK;
  delp->color = RBTREE_RED;
  return true;
}

bool borrowKey(rbtree *t, node_t *delgp, node_t *delp, node_t *del, node_t *sib)
{
  node_t *sibrc;
  if (is2Node(sib))
    return false;
  if (del->key > sib->key)
  {
    if (sib->left && sib->left->color == RBTREE_RED)
      sibrc = sib->left;
    else // 이거 다른 조건 이나 색깔 생각 안하고 그냥 오른쪽이라고 찍어도 되는건가ㅏ
      sibrc = sib->right;
  }
  else
  {
    if (sib->right && sib->right->color == RBTREE_RED)
      sibrc = sib->right;
    else // 이거 다른 조건 이나 색깔 생각 안하고 그냥 왼쪽이라고 찍어도 되는건가ㅏ
      sibrc = sib->left;
  }

  if ((delp->key > sib->key) != (sib->key > sibrc->key))
  {
    // double rotation
    rotate(t, sibrc->key, delp);
    rotate(t, sibrc->key, delgp);
    sib->color = RBTREE_BLACK;
    sibrc->color = RBTREE_RED;
  }
  else
  {
    // single rotation
    rotate(t, sib->key, delgp);
    sib->color = RBTREE_RED;
    sibrc->color = RBTREE_BLACK;
  }
  del->color = RBTREE_RED;
  delp->color = RBTREE_BLACK;

  if (head->left->color == RBTREE_RED)
    head->left->color = RBTREE_BLACK;
  return true;
}

void bindNode(node_t *delp)
{
  delp->color = RBTREE_BLACK;
  delp->left->color = RBTREE_RED;
  delp->right->color = RBTREE_RED;
}

key_t swapKey(node_t *del)
{
  node_t *cdd;
  cdd = del->right;
  while (cdd->left)
    cdd = cdd->left;
  del->key = cdd->key;
  return cdd->key;
}

bool delLeafNode(rbtree *t, key_t key, node_t *delp, node_t *del)
{
  if (key == del->key && !del->left && !del->right)
  {
    // (no child)
    free(del);
    if ((key > delp->key || key == delp->key) && delp != head)
      delp->right = NULL;
    else
      delp->left = NULL;
    return true;
  }
  else if (key == del->key) // del = black, tow children = red
  {
    node_t *ret;
    if (del->left)
    {
      del->left->right = del->right;
      ret = del->left;
      ret->color = RBTREE_BLACK;
      free(del);
    }
    else if (del->right)
    {
      del->right->left = del->left;
      ret = del->right;
      ret->color = RBTREE_BLACK;
      free(del);
    }
    if ((ret->key > delp->key || ret->key == delp->key) && delp != head)
      delp->right = ret;
    else
      delp->left = ret;
    return true;
  }
  else if (del->left && key == del->left->key)
  {
    free(del->left);
    del->left = NULL;
    return true;
  }
  else if (del->right && key == del->right->key)
  {
    free(del->right);
    del->right = NULL;
    return true;
  }
  else
  {
    return false;
  }
}

결론

동적 프로그래밍을하면서 dp 테이블을 채울 때, top-down방식으로 recursive하게 접근하는 것과 bottom-up으로 iterative 하게 접근하는 두 방식에 있어서 결국 dp 테이블을 채워지는 순서는 동일하다. 그럼 위에서 내려갔다가 다시 올라가며 dp를 채우느니 bottom-up으로 iterative하게 하는게 stack-overflow 위험도 없이 진행할 수 있다는 점에서 착안하여 rb트리도, 삽입 삭제를 위한 위치를 찾아가면서 처리 후 다시 밸런스를 맞추는 것보다 밸런스를 맞추며 위치를 찾아가는 방식이 더 좋을 것 같다라고 생각했었다.

참고자료 해당 영상 자료만 이 방식을 채택하고 있었는데 구현까지 끝내고 코드를 이해하고 보니 단점들이 보이기 시작한다.

rbtree 는 중복된 키 값을 허용하지 않는데 중복된 키 값이 들어온다거나, 삭제하려는 key가 없는 key를 삭제요청을 하더라도 해당 위치를 찾아가며 밸런싱 과정을 거치기 때문에 불필요한 rotation 현상들이 발생한다.

또한 가장 처음 들었던 생각 중 어차피 삽입, 삭제 후 밸런싱을 맞출거면 밸런싱 후 삽입, 삭제가 유리하다고 생각했던 이유는 재귀적으로 다시 트리를 아래에서 위로 올라가며 밸런싱을 맞추게 되는 부분이 비효율적이라고 생각했는데 이미 balance가 맞춰져있는 rb트리기에 알고리즘을 풀때 처럼 삽입, 삭제한 leaf node에서 root노드까지 매번 다시 올라오며 밸런스를 맞추는게 아님을 알게 되었다.

또한 삽입, 삭제 후 밸런싱은 직관적이지만 내가 구현한 방식은 나중에는 밸런스가 맞아야하기에 그를 위해 다양한 조건들을 따지고 그에 대한 처리를 하다보니 직관적이지 못한 부분도 있다. 코드 또한 더 많이 작성해야하며 if 조건문들을 더 많이 걸어준다.
이와 관련하여 내 생각이 맞는지 내가 택했던 방법에 대해 보다 자료를 찾아보고 싶어서 위 참고자료를 제공한 분에게 메일을 드려봤고 내 생각과 크게 다르지 않는 것 같다..!! 비록 실무에서 RB트리를 구현한다면 내가 구현한 방식이 아닌 다른 방식으로 구현해야겠지만
삽입, 삭제할 데이터가 어디있는지도 모르면서 밸런싱을 먼저한다는 개념이 재밌었다. 좋은 강의를 올려주신 Jake lee님께 감사드린다.