
- Propositions[명제]
- declarative senetence that is either true or false
- Logical Connectives(연결사), logical operator (논리 연산자)
Negation [부정]
- 한 명제에 대하여 그것이 "아님"을 나타낸다. 따라서 명제가 참이면 그의 부정은 거짓이 되며, 명제가 거짓이라면 그의 부정은 참이 된다.
- 명제 P의 부정은 ∼P, ¬P, NOT P, P' 등으로 기호화
Conjunction [논리곱]
- 두 명제의 논리곱은 모두가 참일 때만 참이 되며, 어느 하나라도 거짓이면 거짓이 된다.
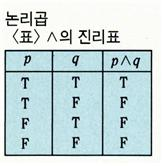
- P 와 Q의 논리곱은 P∧Q, P&Q, P AND Q, P•Q, PQ 등으로 기호화
Disjunction [논리합]
- 모두가 거짓일 때만 거짓이 되며, 어느 하나라도 참이면 참이 된다.
- P와 Q 의 논리합은 P∨Q, P OR Q, P+Q 등과 같이 기호화
Exclusive Disjunction [배타적 논리합]
- 두 개의 명제 중 어느 하나만이 참일때 결과값이 참이 되는 경우를 배타적논리합이라고 한다. 즉, 두 명제가 모두 참이거나 거짓이면 그 결과는 거짓이 된다
- exclusive or 는 P△Q, P EOR Q, P XOR Q, PQ 등으로 기호화
Implication [함축]
- 'P →Q' 는 조건명제로서 '(만일) P이면 Q 이다.' 라고 읽는다.
- P가 참이고 Q 가 거짓일 때만 P → Q는 거짓이 된다. 즉, 조건명제는 전건이 거짓인 경우이거나 후건이 참인 경우에 참인 진리값을 갖는다(함의원리)
- 함의는 P→Q, P⇒Q, P⊃Q 등으로 기호화
- P → Q 다른 표현 방법 :
if p, then q / p implies q / if p, q / p only if q / q unless not p / q when p / q if p / q whenever p / q follows from p / p is sufficient for q / q is necessary for p / a necessary condition for p is q / a sufficient condition for q is p
cf ) p only if q : q가 진실이 아닐 때, p가 진실이 될 수 없다.
Biconditional [쌍조건문,동치]
- P ↔ Q는 P, Q 모두가 같은 진리값을 가질 때만 참
- (P → Q) ∧ (Q → P)인 경우
- 'P이면 Q이고, Q 이면 P이다' 혹은 'P는 Q 이기 위한 필요충분 조건이다' 라고 읽는다
- 동치는 P↔Q, P = Q, P≡Q, P⇔Q 등으로 기호화
- P ↔ Q 다른 표현 방법 : p if and only if q , p is necessary and sufficient for q , if p then q, and conversely, p iff q, p exactly when q
- 역 , 이, 대우
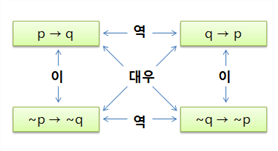
converse [역] ( q → p )
inverse [이] ( ¬P → ¬q )
contrapositive [대우] ( ¬q → ¬p )
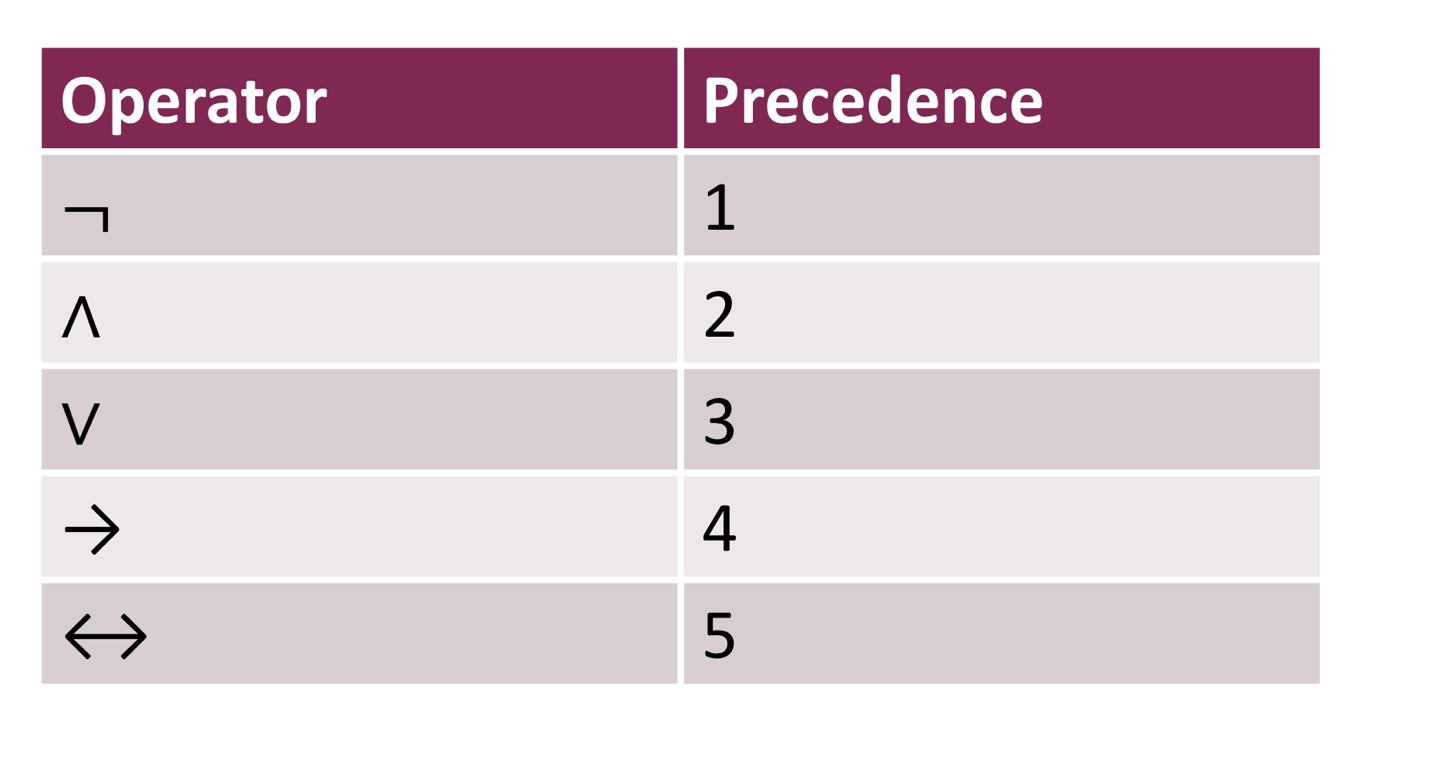
- 논리 연산자 우선순위 (Precedence of Logical Operators)
- 명제 동치 (Propositional Equivalences)
tautology
- 언제나 'True'
Contradiction
- 언제나 'False'
contingencies
Logical equivalence
Normal Forms (DNF, CNF)
- DNF : 분리성 , 마지막에 OR로 구성
- CNF : 결합성 , 마지막에 AND로 구성
Propositional Satisfiability
Key Logical Equivalences
드모르간 법칙
- ¬(P∧Q) ≡ ¬p ∨ ¬q
- ¬(P∨Q) ≡ ¬p ∧ ¬q
Commutative Laws (교환 법칙)
Associative Laws (결합 법칙)
Distributive Laws (분배 법칙)
Absorption Laws (흡수 법칙)
- P∨(P∧Q) ≡ P


