[자료구조] 그래프(Graph)

그래프란?

• 노드(Node) 또는 정점(vertex) 와 노드와 노드를 연결하는 간선(Edge) 으로 구성

✔ 관련 용어

• 정점(vertex) : 위치라는 개념
• 간선(edge) : 위치 간의 관계 , 노드를 연결하는 선(link, branch)
• 인접 정접(adjacent vertex) : 간선에 의해 직접 연결된 정점
• 정점의 차수(degree) : 무방향 그래프에서 하나의 정점에 인접한 정점의 수
  => 무방향 그래프에서 존재하는 정점의 모든 차수의 합 = 그래프의 간선 수의 2배
• 진입 차수(in-degree) : 방향 그래프에서 외부에서 오는 간선의 수
• 진출 차수(out-degree) : 방향 그래프에서 외부로 향하는 간선의 수
• 경로 길이(path length) : 경로를 구성하는데 사용된 간선의 수
• 단순 경로(simple path) : 경로 중 반복되는 정점이 없는 경우
• 사이클(cycle) : 단순 경로의 시작 정점과 종료 정점이 동일한 경우

✔ 그래프 종류

무방향 그래프 VS 방향 그래프

무방향 그래프(Undirected Graph)

• 무방향 그래프는 방향이 없는 그래프로 간선을 통해 양방향 모두 접근 가능
• (A,B) = (B,A)

방향 그래프(Directed Graph)

• 간선에 방향성이 존재
• (A,B) != (B,A)

가중치 그래프
가중치 그래프(Weighted Graph)

• 간선에 비용이나 가중치가 할당된 그래프

연결 그래프 VS 비연결 그래프

연결 그래프(Connected Graph)

• 무방향 그래프에 있는 모든 정점쌍에 대하여 항상 경로가 존재하는 경우

비연결 그래프(Disconnected Graph)

• 무방향 그래프에서 특정 정점쌍 사이에 경로가 존재하지 않는 경우

완전 그래프
완전그래프(Complete Graph)

• 그래프에 속해 있는 모든 정점이 서로 연결되어 있는 그래프
• 무방향 완전 그래프
  => 정점수 : n * (n -1) / 2 {n = 간선의 수}

✔ 그래프의 구현

1. 인접 행렬(Adjacency Matrix)

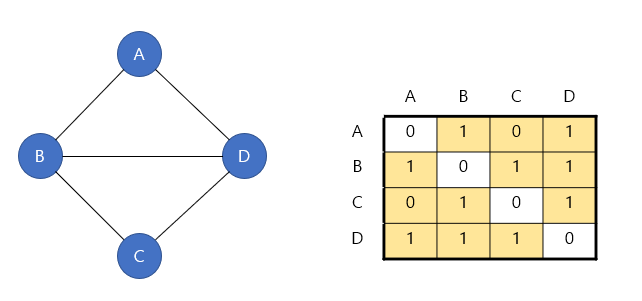
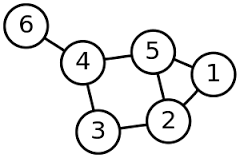
< 무방향 그래프 인접 행렬 표현>

if(간선 x,y가 그래프에 존재) M[x][y] = 1;
otherwise M[x][y] = 0

#include <stdio.h>
#include <stdlib.h>

#define VERTICES 6 //vertex 개수

void printIncidence(int ** g, int v) {
	if (v < 1 || v > 6 ) {
		printf("-1\n");
		return;
	}
	for (int i = 1; i <= VERTICES; i++) {
		if (g[v][i] != 0) printf(" %d %d", i, g[v][i]);
	}
	printf("\n");
}

void makeEdge(int** g, int v1, int v2, int w) {

	if (v1 < 1 || v1 > VERTICES || v2 < 1 || v2 > VERTICES) {
		printf("-1\n");
		return;
	}
    //무방향그래프
	g[v1][v2] = w;
	g[v2][v1] = w;
}

void makeGraph(int** g) {
	
	for (int i = 1; i <= VERTICES; i++) {
		for (int j = 1; j <= VERTICES; j++) {
			g[i][j] = 0;
		}
	}
	//간선 삽입 예시
	makeEdge(g, 1, 2, 1); // 1과 2 사이에 가중치 1인 간선 생성
	makeEdge(g, 1, 3, 1); // 1과 3 사이에 가중치 1인 간선 생성
	makeEdge(g, 1, 4, 1); // 1과 4 사이에 가중치 1인 간선 생성
	makeEdge(g, 1, 6, 2); // 1과 6 사이에 가중치 2인 간선 생성
	makeEdge(g, 2, 3, 1);
	makeEdge(g, 3, 5, 4);
	makeEdge(g, 5, 5, 4);
	makeEdge(g, 5, 6, 3);
}
int main() {
	char c;
	int v, v2, w;
	int** g = (int *)malloc(sizeof(int*) * (VERTICES + 1));

	for (int i = 1; i <= VERTICES; i++) {
		g[i] = (int*)malloc(sizeof(int) * (VERTICES +1 ));
	}

	makeGraph(g);

	return;
}

다음과 같이 표현 할 수 있다.

2. 인접 리스트(Adjacency List)

• 가장 일반적인 방법

#include <stdio.h>
#include <stdlib.h>

#define VERTICES 6 //vertex 개수

typedef struct incidence {
	int weight;
	int vertex;
	struct incidence* next;
}incidence;

typedef struct vertex {
	incidence * head;
	int vertex;
}vertex;

typedef struct graph {
	vertex vertexs[VERTICES + 1];
}graph;

void printIncidence(graph* g, int v) {
	incidence* temp;
	if (v <= 0 || v > VERTICES) {
		printf("-1\n");
		return;
	}
	temp = g->vertexs[v].head->next;
	while (temp) {
		printf(" %d %d", temp->vertex, temp->weight);
		temp = temp->next;
	}
	printf("\n");
}

void printGraph(graph* g) {
	incidence* temp;
	
	for (int i = 1; i <= VERTICES; i++) {
		printf("graph < %d > : ", i);
		temp = g->vertexs[i].head->next;
		while (temp) {
			printf(" %d", temp->vertex);
			temp = temp->next;
		}
		printf("\n");
	}
	printf("\n");
}

//간선 삭제 수정 삽입 모두 가능 + 정점 크기 순으로 삽입됨
void makeEdge(graph* g, int v1, int v2, int w) {
	incidence* temp1,* temp2;
	incidence* new1, * new2;
	incidence* prev1, * prev2;
	int plus = 0;
	temp1 = g->vertexs[v1].head;
	temp2 = g->vertexs[v2].head;
	
	// 정점 존재하지 않을 시 종료
	if (v1 <= 0 || v1 > VERTICES || v2 <= 0 || v2 > VERTICES) {
		printf("-1\n");
		return;
	}
	prev1 = g->vertexs[v1].head;
	prev2 = g->vertexs[v2].head;
	//삭제의 경우
	if (w == 0) {
		while (temp1) {
			if (temp1->vertex == v2) {
				prev1->next = temp1->next;
				free(temp1);
				break;
			}
			prev1 = temp1;
			temp1 = temp1->next;
		}
		while (temp2) {
			if (temp2->vertex == v1) {
				prev2->next = temp2->next;
				free(temp2);
				break;
			}
			prev2 = temp2;
			temp2 = temp2->next;
		}
		return;
	}
	new1 = (incidence*)malloc(sizeof(incidence));
	new1->vertex = v2;
	new1->weight = w;
	new1->next = NULL;

	new2 = (incidence*)malloc(sizeof(incidence));
	new2->vertex = v1;
	new2->weight = w;
	new2->next = NULL;


	//삽입 or 수정
	while (temp1) {
		//삽입
		
		if (temp1->vertex > v2) {
			break;
		}
		//수정 (간선 가중치 수정도 가능)
		if (temp1->vertex == v2) {
			temp1->weight = w;
			plus = 1;
			break;
		}
		prev1 = temp1;
		temp1 = temp1->next;
	}
	if (plus == 0) {
		prev1->next = new1;	
		if (temp1 != NULL) {
			new1->next = temp1;

		}
	}

	while (temp2) {
		//삽입
		if (temp2->vertex > v1) {
			break;
		}
		//수정 (간선 가중치 수정도 가능)
		if (temp2->vertex == v1) {
			temp2->weight = w;
			plus = 1;
			break;
		}
		prev2 = temp2;
		temp2 = temp2->next;
	}
	if (plus == 0) {
		prev2->next = new2;
		if (temp2 != NULL) {
			new2->next = temp2;
		}
	}
}

void makeGraph(graph * g) {
	//초기화
	for (int i = 1; i <= VERTICES; i++) {
		g->vertexs[i].vertex = i;
		g->vertexs[i].head = (incidence*)malloc(sizeof(incidence));
		g->vertexs[i].head->vertex = 0;
		g->vertexs[i].head->weight = 0;
		g->vertexs[i].head->next = NULL;
	}
    //예시
	makeEdge(g, 1, 2, 1); // 1과 2 사이에 가중치 1인 간선 생성
	makeEdge(g, 1, 3, 1); // 1과 3 사이에 가중치 1인 간선 생성
	makeEdge(g, 1, 4, 1); // 1과 4 사이에 가중치 1인 간선 생성
	makeEdge(g, 1, 6, 2); // 1과 6 사이에 가중치 2인 간선 생성
	makeEdge(g, 2, 3, 1);
	makeEdge(g, 3, 5, 4);
	makeEdge(g, 5, 5, 4);
	makeEdge(g, 5, 6, 3);
}

✔ 인접 행렬 VS 인접 리스트

뭐가 더 효율적인가?

• 희소 그래프 VS 밀집 그래프

=> 희소 그래프
만약 정점이 1000개가 있는데 간선은 10개 뿐인 그래프가 있다고 하자. 이렇게 간선의 수가 적은 그래프를 희소 그래프(sparse graph)라고 한다. 이를 행렬로 구현하기위해서는 10개의 간선을 나타내기 위해 1000x1000행렬을 사용해야한다. 하지만 인접 리스트로 구현시 1000 + 10개의 노드만 있으면 구현이 가능하다. 따라서 인접 리스트는 희소 그래프를 표현할때 적당하다.

=> 밀집 그래프
만약 정점이 1000개가 있는데 간선이 2000개가 있는 그래프가 있다고 하자. 이렇게 간선 수가 가 많은 그래프를 밀집 그래프(dense graph)라고 한다. 이때는 인접행렬로 그래프를 구현하는 것이 더 효과적이다. 왜냐하면 행렬은 인덱스로 바로 접근이 가능하기 때문이다