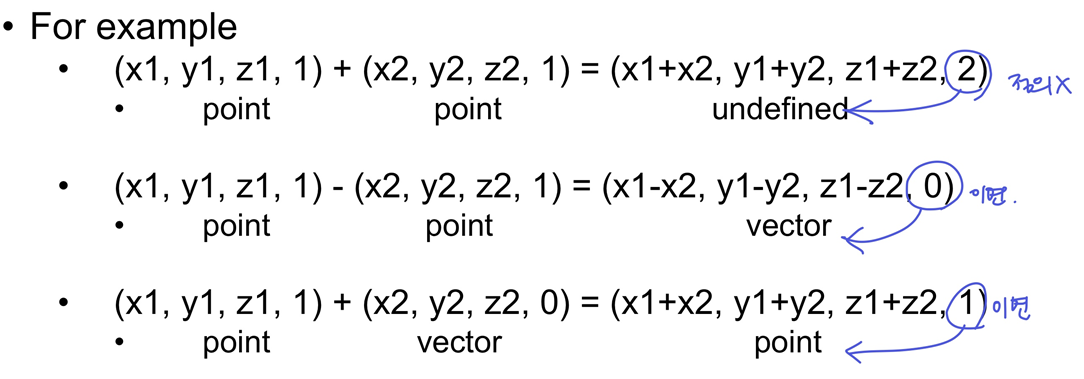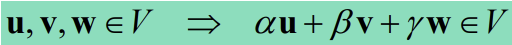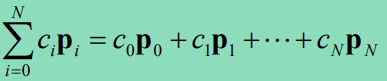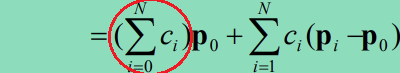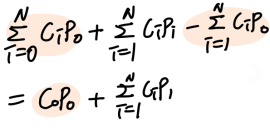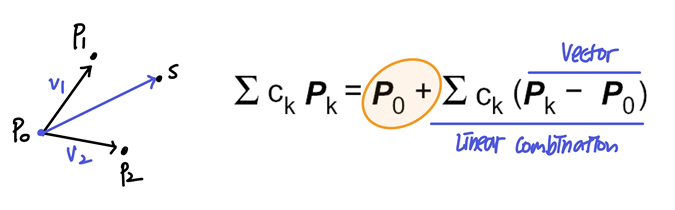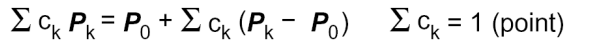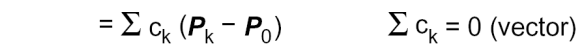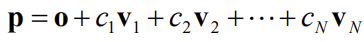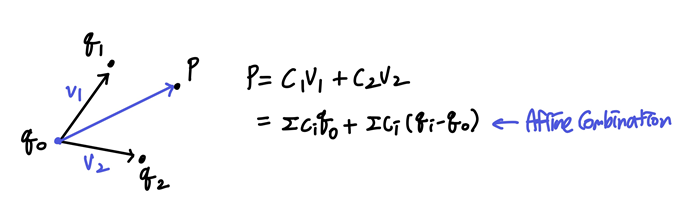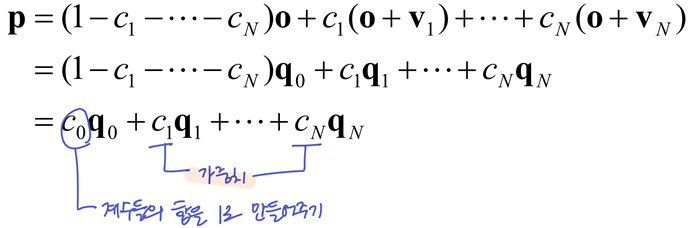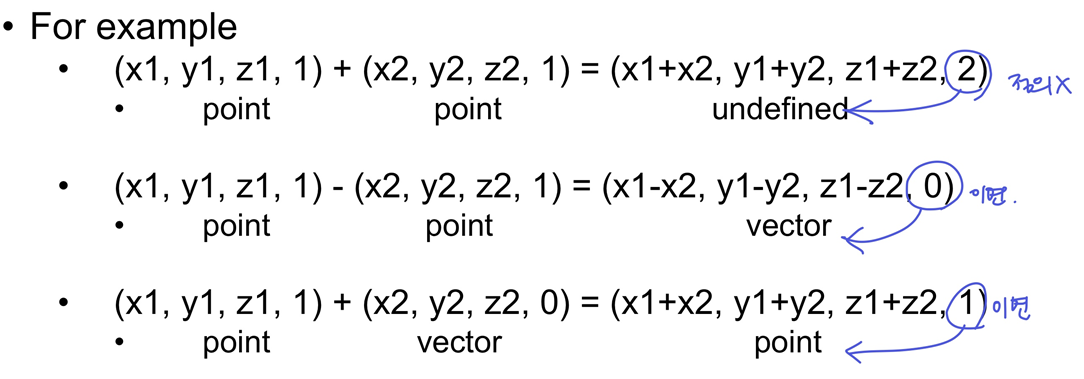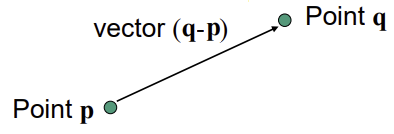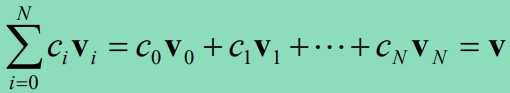[애니메이션이론] 1. Affine Geometry

👀 Coordinate-free Geometry
⚫ Geometric Programming
- 기하학을 프로그래밍하기 위하여 모든 것을 수치화할 필요가 있음 -> vector, point, transform과 같이 숫자로 나타내기
- geometric entities: Vector, Point, Transform
- Homogenous coordinates 사용
- affine geometry와 coordinate-free geometric programming을 다루기
ex) Coordinate-dependence
- 기하학의 기본인 점
- 두 점을 더하는 방법 중 Vector Sum
- (x1+x2, y1+y2)
- 각 점이 원점으로부터의 벡터로 여겨짐
- coordinate frame(축과 원점의 위치 및 방향)이 달라지면 다른 결과
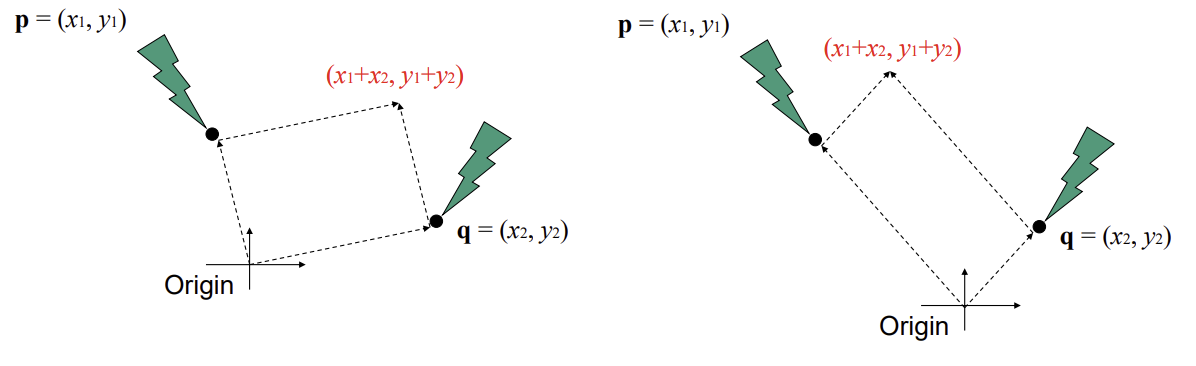
- coordinate frame이 달라도 같은 결과를 얻을 수 없을까?
⚫ Vector and Affine Space
Vector
- Point: coordinate value로 나타낸 position
- Vector: 두 점 사이 위치의 차이(변위)를 나타낸 값
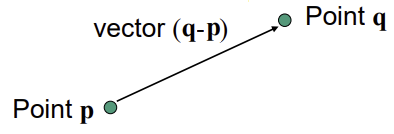
- 원점이 정해지면, Point는 원점으로부터의 Vector로 나타낼 수 있음
- 하지만, Point는 cordinate-free concept에서는 vector가 아님
1. Vector space
- vector와 관련 연산을 포함
- No points (위치X)
-> 위치가 달라도 같은 벡터
- 가능한 Operation: 벡터들의 합, 벡터의 스칼라 곱
- Linear combination of vector = (is also) vector
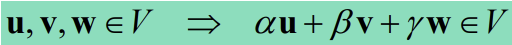
2. Affine space
- vector, 관련 연산, point 포함
- 벡터에 점(위치)개념를 추가
- Vector space를 포함하는 더 큰 개념
- 가능한 Operation
- 두 점의 차이: p에서 q까지의 변위
q-p=v
- 포인트에 벡터 더하기:
p+v=q(p에서 v만큼 가면 q)
- 점끼리의 합은 정의 X
⚫ Affine Combination
- Coordinate-Free Geometric에서 가능한 Operations 5가지
- Addition
- 벡터+벡터=벡터
- 점+벡터=점
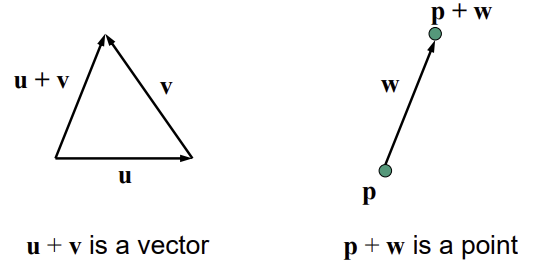
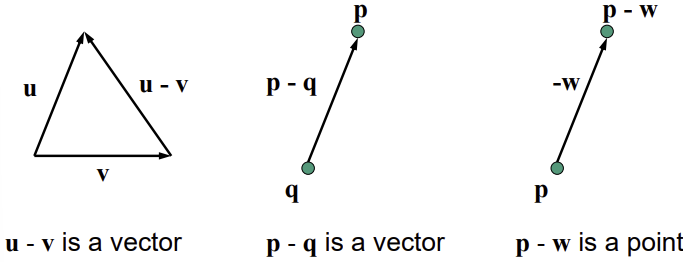
- Subtraction
- 벡터-벡터=벡터
- 점-점=벡터
- 점-벡터=점
- Scalar multiplication
- 스칼라•벡터=벡터
- 점의 곱은 2가지의 예외 제외하고 정의X
- 1•점=점
- 0•점=벡터(0벡터) p−p=(1−1)•p=0•p

- Linear combination
- Linear space: vector space의 subset
- Linear combination: 기저(bases)벡터에 스칼라곱하고 벡터끼리의 합을 하며 새로운 벡터를 만들 수 있음
-> 기저 벡터로 span할 수 있는 공간을 Linear space, 이 때 사용하는 연산을 Linear combination 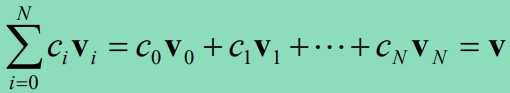
- 벡터 2개로 2차원 평면, 3개로 3차원 공간... (각 벡터가 겹치지 않는 경우)
5. Affine combination✨
- 벡터의 Linear combination처럼, point에도 비슷한걸 적용해보자
- vector space에서는 벡터 1개로 line을 만들 수 없다 -> 공간 상에 점이라는 개념이 없었기 때문
- 점p에 상수c를 곱해서 더하는 것은 원래 되지 않는다.
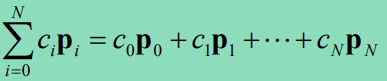
- 하지만, 상수c의 합이 0 또는 1일 때 점p와 곱하는 것은 가능
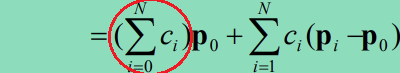
- 아래식을 전개하면 위의 식이 그대로 나온다.
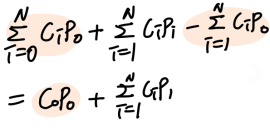
- 점
p0을 기준으로 다른 점과 벡터를 만들고, 그 벡터들과의 Linear combination으로 얻은 벡터를 점 p0과 더하여 새로운 점을 얻는 것!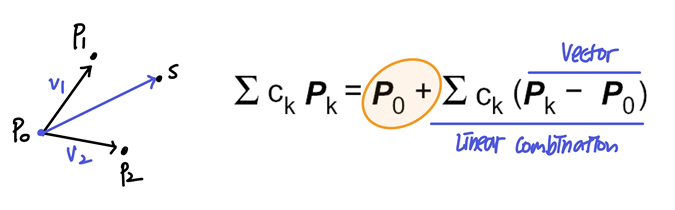
- 계수의 합 부분이 1인 경우를 Affine combination이라고 함
- 점 + 벡터 = 점
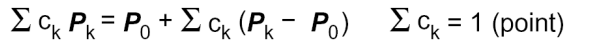
- 계수의 합 부분이 0인 경우는 따로 통칭하지 않음
- 벡터 + 벡터 = 벡터
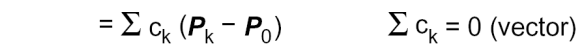
- 계수의 합 부분이 0 또는 1이 아닌 경우는 정의 X

- 따라서, 점 2개로 직선, 점 3개로 평면 등.. 점들의 스칼라곱과 합으로 다른 점들을 만들 수 있음
- 직선상의 두 점은 Affine combination이 가능한 것, 점 2개로 직선 상의 모든 점을 만들 수 있다
- example
- (p+q)/2
-> 계수의 합=1, 선pq의 중점
- (p+q)/3
-> 계수의 합≠1, 기하학적 의미를 지니지 X
- (p+q+r)/3
-> 계수의 합=1, 삼각형pqr의 무게중심
- (p/2+p+2-r)
-> 계수의 합=0, 점r에서 선pq의 중점으로 가는 벡터 (vector combination)
⚫점의 수치화
1. Affine Frame
- 기준점(원점)
o에서 점p로 벡터w를 생성
- 벡터
w의 수치화
- w=c1v1+c2v2
- 해당 벡터공간의 기저벡터
v의 Linear combination으로 벡터공간의 모든 벡터들을 c로 나타낼 수 있다(수치화)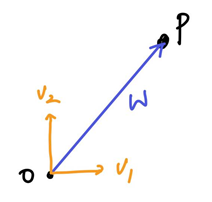
- 점의 수치화는 결국, 기준점을 사용하면 벡터의 수치화와 같다
- 점
p는 여러개의 기저가 주어진 N차원의 벡터공간에서 원점+Linear combination으로 나타낼 수 있다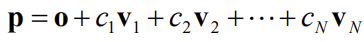
-> p를 계수c들로만 표현할 수 있게 됨
2. Barycentric Coordinates
- 한 점을 아무 기준(원점, 축)없이 다른 점을 활용하여 상대적으로 나타내기
- 점들의 Affine Combination으로 또 다른 점을 나타낸 것을 활용
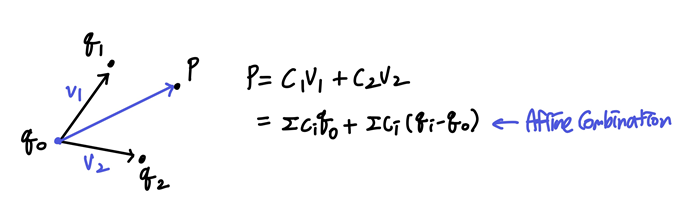
- Affine Combination에서의 Linear combination에서, 각 벡터들을 얼마나 사용하는지에 대한 계수 즉, 가중치
c를 사용해 점을 표현하기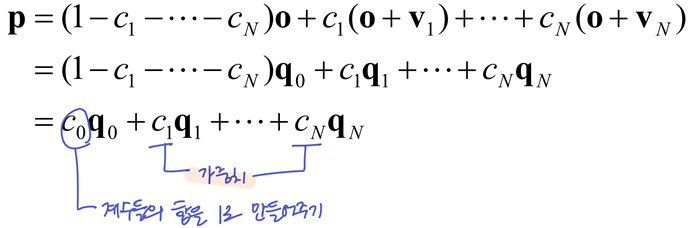
⚫ Homogeneous Vectors
- Homogeneous point는 z자리에 1을 붙였다면, Homogeneous vector에는 z자리에 0을 붙인다

- 점, 벡터의 연산으로 예시를 들어 살펴보면 지금까지 한 내용들이 성립함을 알 수 있다!