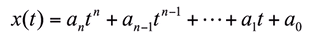⚫ Motion
- 시간에 따라 transformation이 변화하는 것 (time-varying)
- Model(local) coordinate에서 World coordinate로 바꿀 때의 transformation이 시간t에 따른 함수가 되면 모션
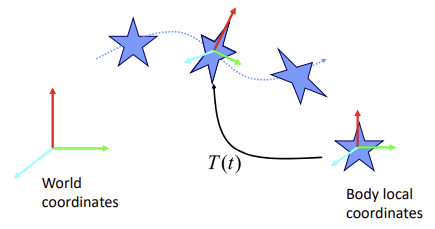
- Model(local) coordinate에서 World coordinate로 바꿀 때의 transformation이 시간t에 따른 함수가 되면 모션
⚫ Keyframing (Keyframe in-betweening)
- keyframe: key가 되는 frame (1초에 한두개 등 주요한 장면)
- Keyframing: keyframe 사이를 자연스럽게 이어주는 것 (컴퓨터가 이어줌)
- 모든
t에 대한 TransformationT를 다 만들어줄 필요 없이, 특정t에 대해서만T를 만들어 주면(keyframe) 나머지 임의의t에 대한T를 계산하는 과정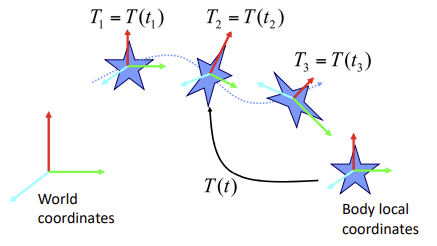
- 모든
Transformation
- Rigid transformation
- 모양, 크기 변화 X
- Rotate + Translate
- ->
- Affine transformation
- Scale + Shear + Rigid Transf.
- ->
- Homogeneous transformation
- Projective + Affine Transf.
- 4x4 homogeneous matrix
- ->
- General transformation
- Free-form deformation
- ex) 공 찌부..
아래는 keyframing을 위해 필요한 것들
⚫ Spline curves
- classical approach: 곡선을 어떻게 수치화 할까?(도면에 그리기 위해)
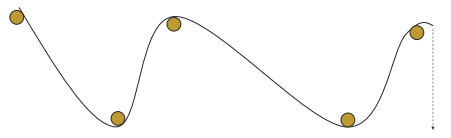
- 말뚝 박아서 철판 끼웠다 생각하면, 말뚝 위치만 잘 정하면 일정한 곡선을 얻을 수 있다
- 이러한 방식으로 점을 고정해서 만든 곡선을 Spline이라고 함
- 곡선은 에너지가 최소화되는 방향으로 모양이 만들어짐
- In geometric model: 철판 말고, 곡선을 나타내기 위해 매개변수
t(시간)에 대한x,y좌표로 나타내자 ->x(t),y(t) - Smoothness: 얼마나 부드러운지.. continuity (는 나중에)
1. Polynomial curve
- 점들을 지나는 다항식을 만들어 곡선 그리기
- 다항식은 여러가지 초월함수에 비해 간단하며, 미분 가능하다는 다양한 장점이 존재
- 어떤 점이 t에 대하여 변화하고 있을 때, t에 대한 좌표를 나타내는 함수
x(t),y(t),z(t)를 다항식으로 표현 (parametric polynomial, parametric curve)- 다항식의 계수에 따라 곡선의 모양 결정
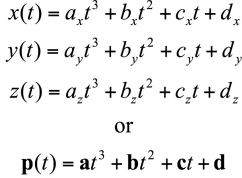
- 다항식의 계수에 따라 곡선의 모양 결정
Polynomial
- Degree(차수): n
- Order(항수): n+1 = 계수의 개수
◾ Polynomial Interpolation
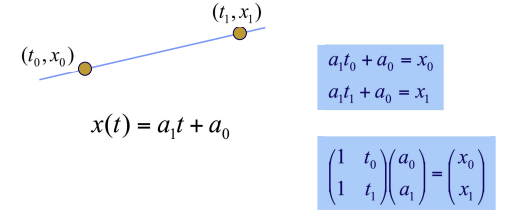
- 두 점을 지나는 선: 2개의 식(constriant 2개), order 2, degree 1 -> 일차식
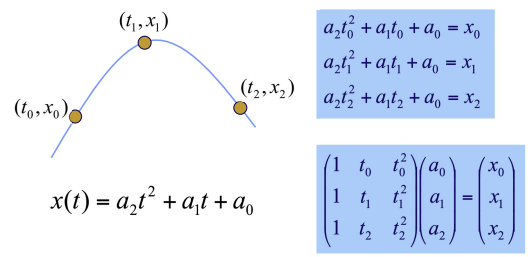
- 세 점을 지나는 선: 3개의 식, order 3, degree 2 -> 이차식
- n+1개
0~n의 점을 지나는 선: n+1개의 식, order n+1, degree n -> n차식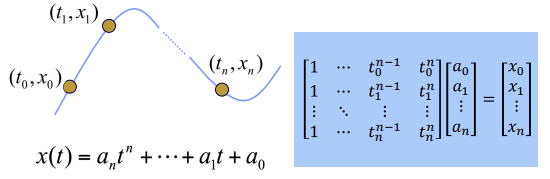
- 차수가 커지며 복잡해졌으므로 행렬로 풀어나가고, 역행렬 계산 필요
❗ 결국 점을 계산하여 선 상의 모든 점을 만들 수 있는 Affine Combination이다. (Lagrange Polynomial에서는 이걸로 접근해보자는 것)
2. Lagrange Polynomial curve
- 복잡한 역행렬 계산보다 간단한 방법
- 위와 다른 접근, Affine Combination으로 접근하여 다항식을 만들기
- n개의 점을 지나는 곡선 = n개의 점으로 Affine Combination
- 계수의 합이 1인 Affine sum으로 접근하기 위해 Weight 사용 -> 계수
- 근데 계수가 상수가 아닌 다항식
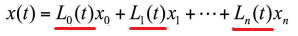
◾ ✨
- 일 때, 이 나오게 하려면 의 계수는 이 되어야하고, 나머지 계수들은 0이 나와야한다
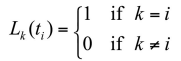
- 이 아닐 때는 분자가 0이 나오도록 하고, 일 때는 분모 분자가 약분되어 1이 나오도록 하는 다항식
- 0~n이라서 n+1개의 t가 있지만, 분자에 가 빠져 n개의 t로 이루어진 식 (분모는 상수)
-> t에 대한 n차식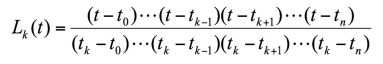
◾ Lagrange Polynomial 총정리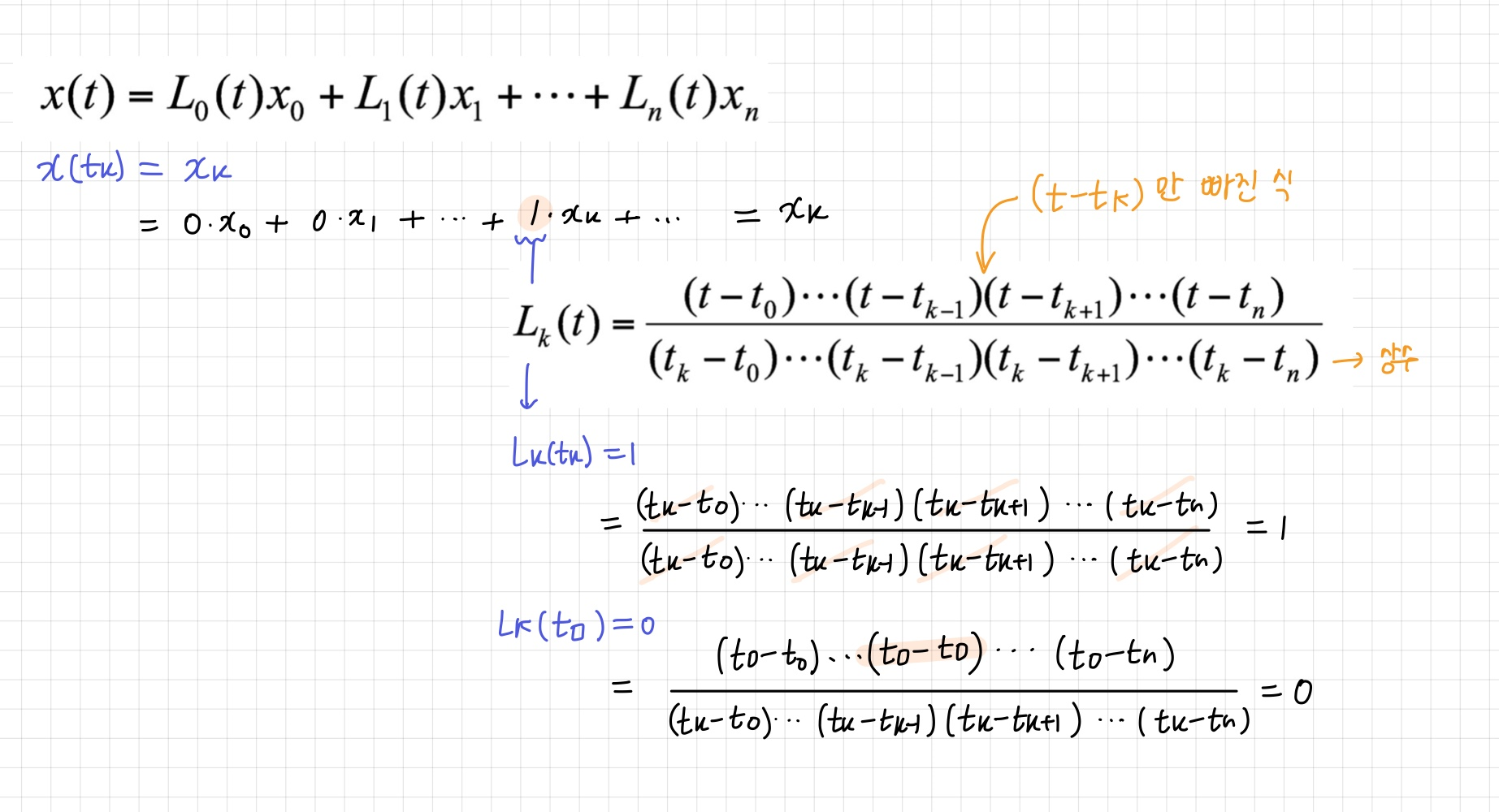
◾ Limitation
- 차수가 너무 높아 자유도가 높아지면 끝부분에 이상한 형태(Oscilation)이 생길 수 있음
3. Piecewise curve
- 차수를 낮추고, 모든 점을 지나게 하려면?
-> 범위를 끊어서 낮은 차수의 곡선을 만들고 이어붙이자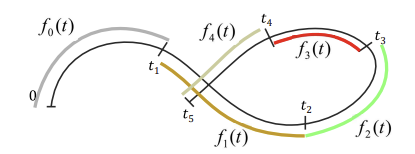
- 곡선을 이어붙인 시간을 knot sequence이라고 함(knot: 매듭)
◾ Defining Spline Curves
- 각 piecewise별 다항식
f(t)은 주로 3차 곡선(cubic)을 사용함 - 각 영역마다 다른 계수를 갖게되는 것
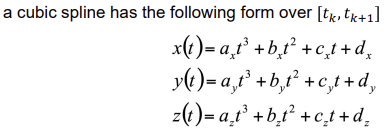
◾ Control of Spline Curves
- knot sequence의 점은 곡선의 모양을 결정하는 점으로 Control Points라고 부른다
- 이걸로 다각형 만들면 Control polygon
- Control Points를 어떻게 사용하느냐(아래 3가지)에 따라 결정되는 모양
- Interpolating
- Control Points를 모두 지나면서 자연스러운 곡선
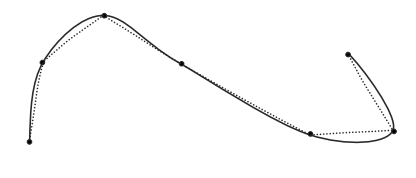
- Control Points를 모두 지나면서 자연스러운 곡선
- Approximation
- Control Points들이 간접적으로 점 근처의 곡선의 모양만 결정
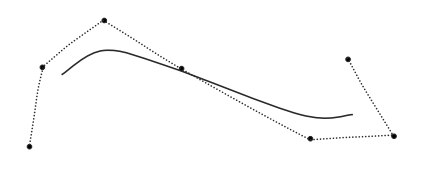
- Control Points들이 간접적으로 점 근처의 곡선의 모양만 결정
- Interpolating some control points
- 일부의 점은 지나가고, 나머지 점은 모양 잡는데 사용하고
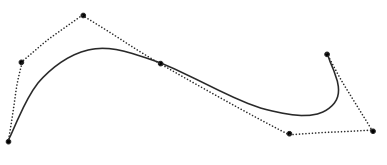
- 일부의 점은 지나가고, 나머지 점은 모양 잡는데 사용하고
3-1. Piecewise Linear curves
- 각 segment를 1차식으로 연결할 때의 식
- 각 범위를 t0, t1, ...이 아니라 [0, 1]로 생각해보면
- 0일 때 x0, 1일 때 x1이 나와야하고 아래와 같이 a, b를 유도할 수 있음
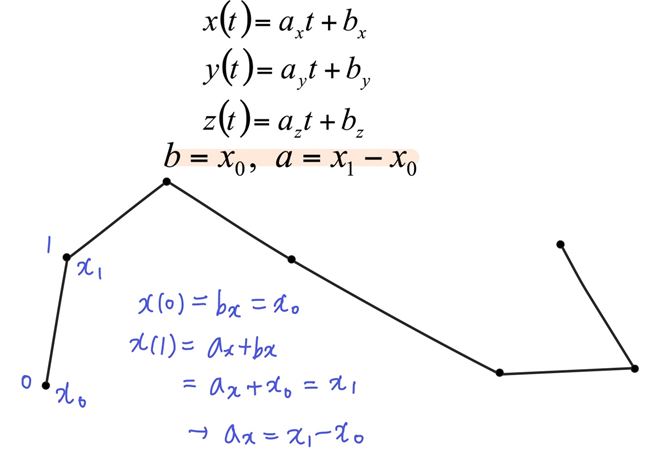
- 0일 때 x0, 1일 때 x1이 나와야하고 아래와 같이 a, b를 유도할 수 있음
- In vector form -> Affine geometry
- 두 점 사이 벡터의 크기를 t에 따라 0~1로 키워가면서 원점에 더해 두 점 사이의 점들을 구할 수 있음
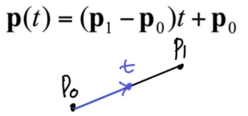
- 두 점 사이 벡터의 크기를 t에 따라 0~1로 키워가면서 원점에 더해 두 점 사이의 점들을 구할 수 있음
- In matrix form
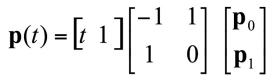
- 위의 식을 더 간단하게 하면
- Basis function form -> Affine Combination
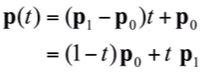
- Matrix version
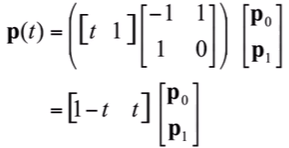
- Basis function form -> Affine Combination
- 결국, 각 piece는 weight에 따른 두 점의 Affine Combinations으로 만들어진 직선
- Affine이므로 합은 항상 1이다
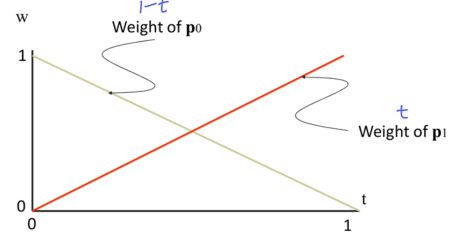
- Affine이므로 합은 항상 1이다
- 전체적으로 보면 점 pn에 해당하는 weight가 tn일 때 1이고, 아래와 같은 형태를 띄며 나머지는 0이 됨
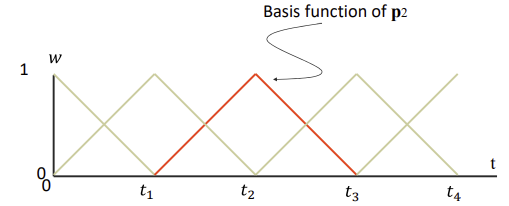
특징
- local control
- Control point를 움직였을 때 해당 직선만 영향이 있고 나머지는 그대로 (Lagrange와 다르게(Oscilation))
- Weight 그래프에서 한 점이 일정 범위를 벗어나면 0이라는 뜻
- Convex
- 직선이 control polygon의 convex hull안에 포함됨
- Continuous
- Control point에서는 만나지만, 미분불가능
Continuous ✨
- n번 미분한 값이 연속
- n계도함수가 연속
3-2. Bezier Segment
- 각 segment를(두 점을) 1차식으로 연결하지 말고 차수를 높여서 곡선을 만들어보자
- 보통 3차 Bezier Curve
- 기존 점들 사이에서 t가 변화할 때의 새로운 점은 어딘가를 알기 위해,
- 두 점 사이 직선을
t:1-t로 내분 -> 3개의 점 - 그 내분점들끼리 연결 -> 2개의 직선
- 그 직선을 또
t:1-t로 내분 -> 2개의 점 - 또 내분점들끼리 연결 -> 1개의 최종 직선
- 최종 직선을 또
t:1-t로 내분 -> 1개의 최종 새로운 점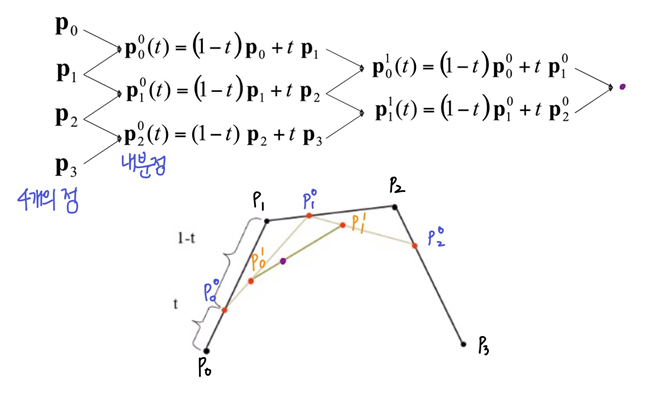
- 두 점 사이 직선을
- t(0~1)를 움직여가며 위의 과정을 반복하다보면 아래와 같은 곡선이 그려진다
- 양쪽 끝 점은 무조건 지나가는 곡선
- 가운데 두 점은 곡선의 모양을 조절
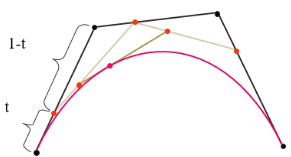
◾ 이항계수 (Binomial function)
- 위 식을 정리하면 아래와 같이 이항계수 형태로 나타남
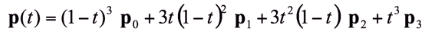
- 차수가 높아지면 아래와 같이 일반화 가능하며, 점에 계수(이항계수)를 곱한 형태로 나타남 (Bernstein Polynomial)
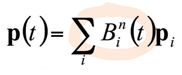
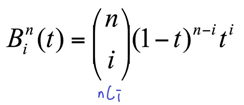
- 각 항의 weight를 나타낸 그래프
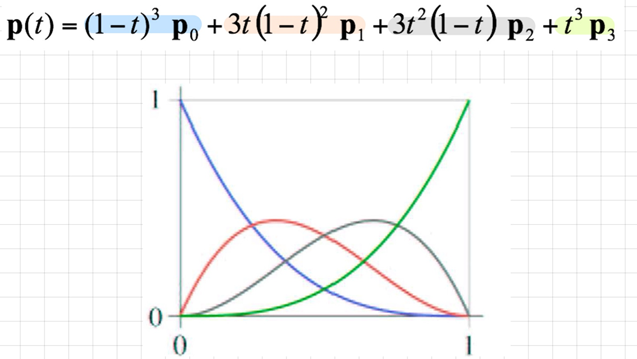
- ti에서 한 개의 항만 1이고, 나머지는 0일 때, 곡선은 점 pi를 지난다
- 양 끝항의 값은 각각 0과 1일 때 본인만 1이고 나머지는 0 (Lagrangian) -> 곡선이 양 끝 점을 지난다
- 중간항의 값은 1이 되지 않는다 -> 곡선이 중간 점은 지나지 않는다
-> Bezier 곡선의 특징이 나타남
◾ 특징
- Convex
- 곡선이 control polygon의 convex hull안에 포함됨
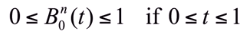
- 이 0~1이라는 것은 외분 불가능하다는 것, 내분만 가능하여 convex hull안에 포함된다는 것이다
- 곡선이 control polygon의 convex hull안에 포함됨
- Affine invariant
- Affine transform에 대하여 invariant
-> control point를 affine transform하고 곡선상의 점을 찾은 결과 = 곡선상의 점을 찾고 affine transform한 결과
(affine하고 곡선 만든 것 = 곡선 만들고 affine한 것) - 이유: 계수의 합이 1이라서 (Affine combination이어서)
- Affine transform은 Affine sum을 보존하는 trasnform이다
- Affine transform에 대하여 invariant
- Variation diminishing
- 임의의 선을 많이 그려봤자, control polygon과 만나는 점의 개수가 곡선과 만나는 점의 개수보다 무조건 많다
- 커브가 많이 우글거리는 애들은 polygon은 안만나는데, 곡선과 만나는 경우가 생김! (ex-Lagrangian)
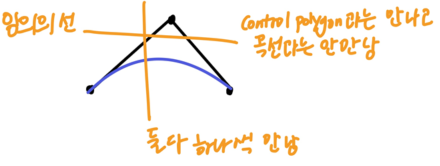
- 커브가 많이 우글거리는 애들은 polygon은 안만나는데, 곡선과 만나는 경우가 생김! (ex-Lagrangian)
- 커브가 쓸데없이 우글거리지 않음
- 변화가 줄어든다
- 임의의 선을 많이 그려봤자, control polygon과 만나는 점의 개수가 곡선과 만나는 점의 개수보다 무조건 많다
- End point interpolation
- 0 넣으면 0번째꺼
- 1 넣으면 3번째꺼
◾ Blossom
- 6번의 내분 과정에서, 내분할때마다 t 바꾸기
3-3. Hermite Spline
◾ Cubic Hermite Interpolation
- 일반적인 함수를 Approximation하는 다항함수를 만들기 중 하나 (다루기 쉽고 계산하기 쉬움)
- 두 점과 각 탄젠트가 있을 때, 탄젠트 방향으로 곡선
- 점에 대한 식 2개, 탄젠트에 대한 식 2개
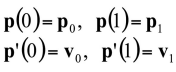
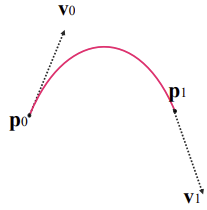
- 점에 대한 식 2개, 탄젠트에 대한 식 2개
- 3차 다항식의 계수
a, b, c, d를 알아내기 위해 위의 4개의 식을 활용
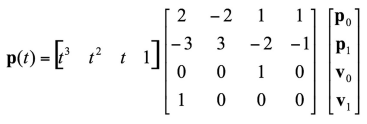
◾ vs Bezier curve ✨
- Bezier와 Hermite 둘 다 t에 대한 3차식
- Bezier form을 미분
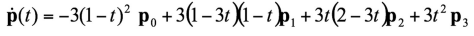
- 미분식에 0을 넣으면 Bezier curve의 t=0일 때 tangent
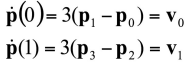
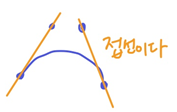
- 미분식에 0을 넣으면 Bezier curve의 t=0일 때 tangent
- Bezier와 Hermite는 같다
- Bezier는 점을 준 것
- Hermite는 벡터를 준것
- ex) Hermite interpolation을 위해 벡터
v가 주어진 경우, 그 벡터로 Bezier curve의 두 점을 찾으면 된다
◾ Piecewise cubic Hermite Interpolation
- 각 segment의 curve를 연결할 때, Bezier 대신 각 점의 tangent를 사용하여 Hermite로 그리기
- 한 segment의 끝 점의 tangent = 다음 segment의 첫 점의 tangent -> 자연스러운 곡선
(만나는 점에서의 tangentv를 똑같이 만듦)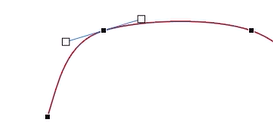
◾ 특징
- Affine invariant
- local control
- Control point를 움직였을 때, 주변 일부 점에만 영향이 있고 나머지는 그대로
- Weight 그래프에서 한 점이 일정 범위를 벗어나면 0이라는 뜻
- continous
- curve를 붙일 때, 한 점에서의 앞 뒤 tangent가 같으므로 일계도함수가 연속
- Convex (X)
- Control polygon밖으로 나갈 수 있음
(점 세개로 자연스러운 곡선을 그릴 때, 삼각형 안에서 자연스러운 곡선을 그릴 수 없음)- 그래서 variation diminishing도 X
- Interpolation curve는 Convex와 variation diminishing 성질을 가질 수 없음
- 매번 tangent를 주기 어려움, 점으로만 자연스러운 곡선을 만들자 -> Catmull-Rom
3-4. Catmull-Rom Spline
- tangent 조건 없이 Polynomial interpolation
-> 자동 tangent determination
-> tangent를 계산해내기 - 세 점이 있을 때, 가운데의 tangent는 양 끝점의 차이를 시간(2)로 나눈것
-> 거리/시간 = 속도 (두 점 사이를 직선으로 이동할 때의 속도)
-> 두 점으로 그 사이 점들의 속도를 알아내는 것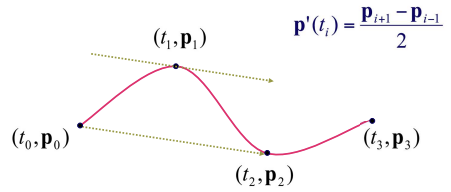
- 사용자는 tangent 정보 없이 점 4개만 주면 됨!
◾ weight 그래프 및 특징
0~음수~0~1~0~음수~0형태- 본인 점일때만 1 -> Interpolation curve
- 점이 일정 t범위를 벗어나면 0 -> local control
- Weight sum = 1 -> Affine Sum, Affine invariant
- 음수의 weight는
0~1를 벗어남 -> Convex와 variation diminishing 성질 X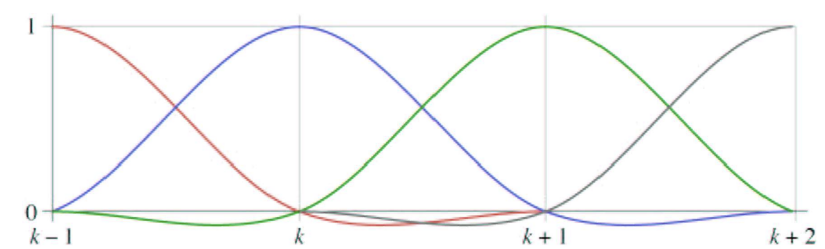
◾ Bessel Tangents
- 끝 점의 Tangent는?
-> 3개의 점 필요 - t=0일 때 tangent를 구하려면, 0, 1, 2번째 점을 지나는 포물선(Parabola)을 계산하고 그때의 tangent 구하기
- 기존 세 점을 지나는 곡선 -> 세 개의 식
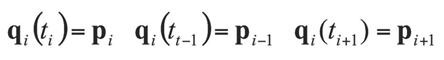
- 위의 조건식을 활용하여 a, b, c를 구하고 식
q(t)완성기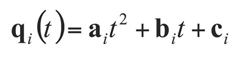
- 식
q(t)를 미분하여 tangent 구하기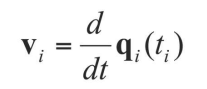
- 기존 세 점을 지나는 곡선 -> 세 개의 식
◾ Overhauser spline
- Bessel tangent를 사용한 Hermite spline 그리기와 같음 (또는 Bezier 그리기)
- 앞의 세 점과 뒤의 세 점으로 각각 2차곡선(포물선)을 만들고, 겹치는 부분의 곡선은 Linear Interpolation한다
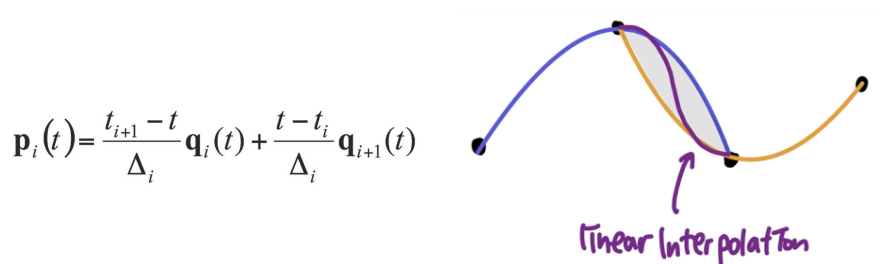
👀 Catmull-Ron 이해하기..
◾ 양끝점의 tangent에 따른 Problem (Code)
-
처음과 끝점의 tangent를 0으로 설정
// 양쪽 점으로 k의 tangent 계산 if( k>0 ) v0 = ( srcPts[k+1] - srcPts[k-1] )/2; else v0 = 0;// k가 가장 처음 처음 점일 때 // 양쪽 점으로 k+1의 tangent 계산 if( k+2<srcPts.size() ) v1 = ( srcPts[k+2] - srcPts[k] )/2; else v1 = 0 // k가 가장 마지막 점일 때- 점으로 나타내보면 처음 시작과 끝부분에 점들이 몰려있음
-> 처음과 끝의 속도가 0이기 때문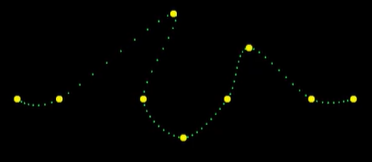
- 이러한 식으로 애니메이션을 만들면 처음엔 거의 멈춰있다가 서서히 움직이기 시작하고, 감속하며 멈추는 모습을 보여줄 것
- 점들이 직선상에 존재하여 등속운동을 해야함에도 불구하고, 처음과 끝에 속도 변화가 생길 것
- 점으로 나타내보면 처음 시작과 끝부분에 점들이 몰려있음
-
처음과 끝점의 인접한 점과의 직선을 따르도록 하기
// 양쪽 점으로 k의 tangent 계산 if( k>0 ) v0 = ( srcPts[k+1] - srcPts[k-1] )/2; else v0 = srcPts[k+1] - srcPts[k];// k가 가장 처음 처음 점일 때 // 양쪽 점으로 k+1의 tangent 계산 if( k+2<srcPts.size() ) v1 = ( srcPts[k+2] - srcPts[k] )/2; else v1 = srcPts[k+1] - srcPts[k]; // k가 가장 마지막 점일 때- 처음 점에서 다음 점으로 갈 때, 쓸데없이 살짝 내려갔다가 올라가는 형태의 곡선

- 처음 점에서 다음 점으로 갈 때, 쓸데없이 살짝 내려갔다가 올라가는 형태의 곡선
-
Bessel tangent 사용
// 양쪽 점으로 k의 tangent 계산 if( k>0 ) v0 = ( srcPts[k+1] - srcPts[k-1] )/2; else { // k가 가장 처음 처음 점일 때 // 연립방정식 ...~ //p(t) = a*t*t + b*t + c //p(0) = c = srcPts[k] //p(1) = a+b+c = srcPts[k+1] //p(2) = 4*a+2*b+c = srcPts[k+2] // 연립방정식 결과 (x, y축 각각하므로 vec2) //vec2 a = ~; //vec2 b = (4*srcPts[k+1] - 3*srcPts[k] - srcPts[k+2])/2; //vec3 c = ~; // p'(t) = 2*a*t + b // p'(t) = b // v0 = b; v0 = (4*srcPts[k+1] - 3*srcPts[k] - srcPts[k+2])/2; } // 양쪽 점으로 k+1의 tangent 계산 if( k+2<srcPts.size() ) v1 = ( srcPts[k+2] - srcPts[k] )/2; else v1 = -(4*srcPts[k] - 3*srcPts[k+1] - srcPts[k-1])/2; // k가 가장 마지막 점일 때- 양 끝 부분의 속도가 일정해짐!! 곡선도 럽

- 양 끝 부분의 속도가 일정해짐!! 곡선도 럽
◾ Continuity
- Piecewise때문에 Continuity가 언급되는 것 -> 만나는 점에서 연속인가?!를 계속 따져봐야함
- zero-order(): 미분 안해도 연속, 곡선이 연결된 부분이 끊어져있지 않고 연속
- first-order(): 1번 미분했을 때 연속, 곡선이 연결된 부분의 tangent가 같다
- second-order(): 2번 미분했을 때 연속 (더 정교하고 자연스러운..)

- : tangent의 방향만 같고 크기만 다른 (여전히 부드러운 곡선 -> 방향만 같으면 자연스럽다!)
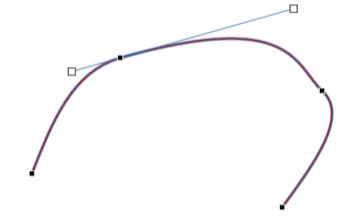
- : tangent의 방향만 같고 크기만 다른 (여전히 부드러운 곡선 -> 방향만 같으면 자연스럽다!)
3-5. B-Spline
- More Continuity -> Continuity + Local control
- Control Point를 Bezier curve의 Control Point로 계산
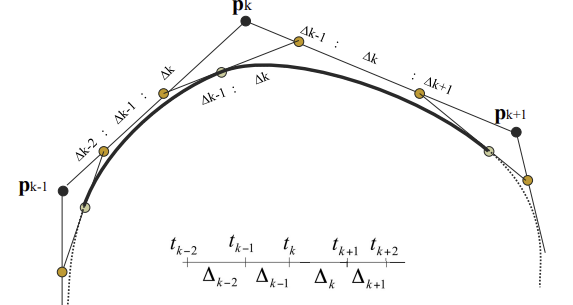
- 네개의 점에 계수가 붙는 t에 대한 3차식 (Affine Sum)
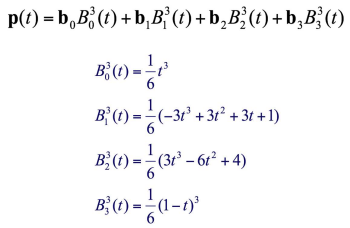
- t일 때 한 segment 곡선의 점을 찾기 위해 4개의 point가 필요
- 각 Control point의 weight 그래프는 Bell-shaped basis function
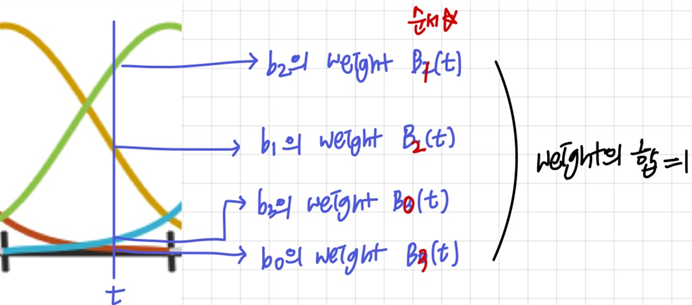
- 각 Control Point
b0,b1,b2,b3의 가중치 를 사용해 식 계산 (weight의 합=1)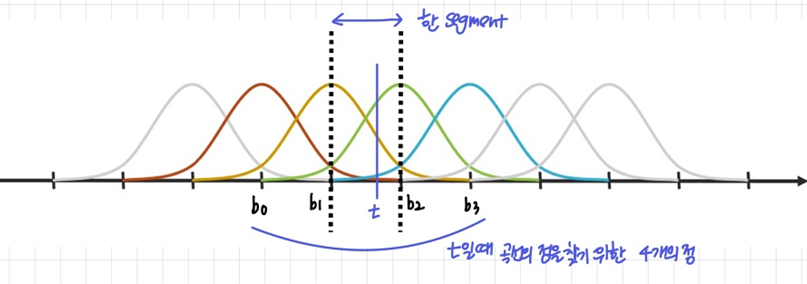
- 각 Control point의 weight 그래프는 Bell-shaped basis function
- t가 0 또는 1인 경우에서도 weight의 합은 1
- weight의 가장 높은 부분이 1이 아님
-> Interpolation 안됨 (Control point를 지나지 않는다!!)✨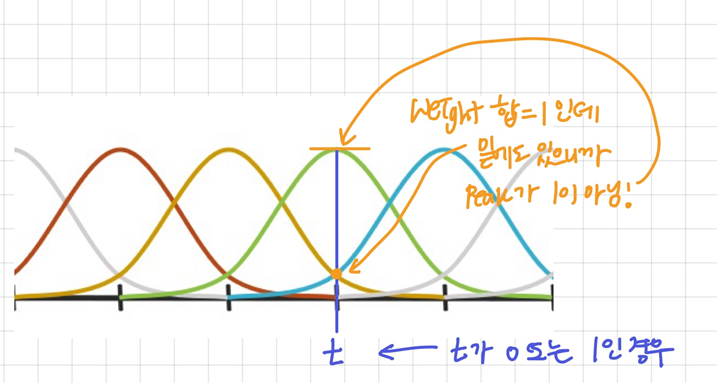
- weight의 가장 높은 부분이 1이 아님
- 지금까지는 t가 0~1 간격일때만 다뤘는데, 간격이 달라지는 경우가 있어서 이를 일반화한 식은 아래와 같다 (recursive한 식)
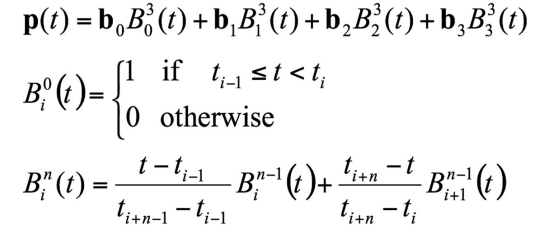
◾ 특징
- Convex
- 계수의 범위가 0~1이므로

- 계수의 범위가 0~1이므로
- Affine invariance
- Affine sum이므로
- Variantion diminishing
- convex hull 특성을 가지고 부드러워서 가질 것 같다....~ (증명은 안된다하심)
- -continuity
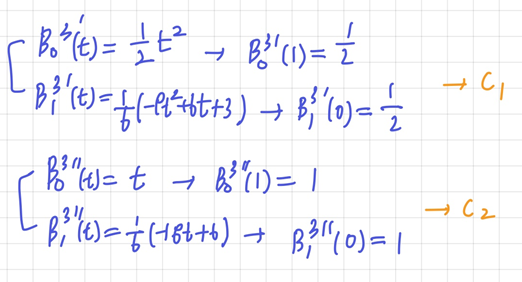
- Local controllability
-curve 바깥 weight가 0