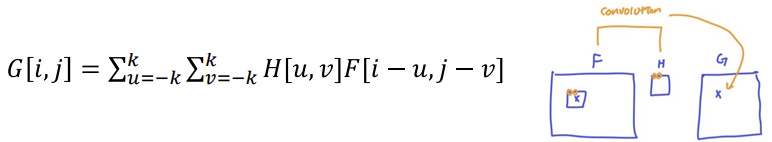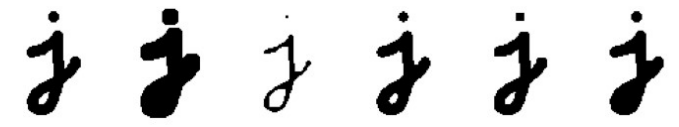Image
- 이미지는 함수 (좌표를 넣으면 밝기값이 나오는)
- 함수 f(x, y)는 점(x, y)의 밝기 ( -> ; 2차원(좌표)에서 1차원(밝기값))
- color image도 함순데 좌표를 넣으면 RGB값이 나오는
- 벡터값 함수 ( ->)
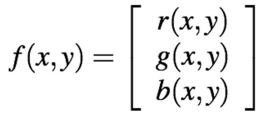
- 벡터값 함수 ( ->)
Digital Image
- Raseter 형태(픽셀별로 저장)
- Discrete (각 픽셀마다 대표되는 값을 얻기 위해 sampling)
- 실수 R 대신 정수로 메모리에 저장(Quantize; round to nearest integer)
- Matrix form
Image Operations
- Input image --
operation--> Output image- Local operator: 출력 image의 한 픽셀을 결정할 때 대응하는 입력 image의 한 픽셀만 고려
- Neighborhood operator: 출력 image의 한 픽셀을 결정할 때 입력 image의 이웃 픽셀 고려 (filter 사용)
- lienar
- nonlinear
1. Local Operator
- point process
- g(x)=h(f(x))
- input
h(x), outputg(x)(x는 벡터) - g(x)=h(f0(x), ... fn(x)) (input image 여러개)
- input
1-1. Pixel transform
- simple point process
- g(x)=af(x)+b
a: gain, contrast (output에 input 영향O)b: bias, brightness (output에 input 영향X)
- spatially varying (위치에 따라 a, b 다르게)
- g(x) = a(x)f(x) + b(x)
- ex) 비네팅 (바깥으로 갈 수록 contrast와 brightness가 낮아짐)
- Linear blend operator
- g(x)=(1-α)f0(x) + αf1(X)
- cross-dissolve (장면 전환)
- Non-linear transform
- gamma correction ([0,1]범위에서 f(x)가 0 또는 1일 때는 γ값에 상관없이 그대로, 중간 값만 변함)
- g(x) = f(x)^(1/γ)
1-2. Color transform
- Luminance
Y(밝기) - simple color transform
- RGB -> YUV
- RGB -> YCrCb
- C: Croma(색상)과 red, blue (음수까지 범위를 가져서 green은 필요X)
- Jpeg, 카메라에서 값 읽어올 때 등 YCrCb 사용
- 밝기Y(흑백) 다루기 쉽기 때문에 자주 사용됨
- Complex transform
- RGB -> XYZ (색을 절대적으로 표현-모니터도 다 색 달라서 특정 기준으로 RGB를 나타낼 수 없으니까..)
- RGB -> Lab (L: 밝기, 사람의 눈과 비슷)
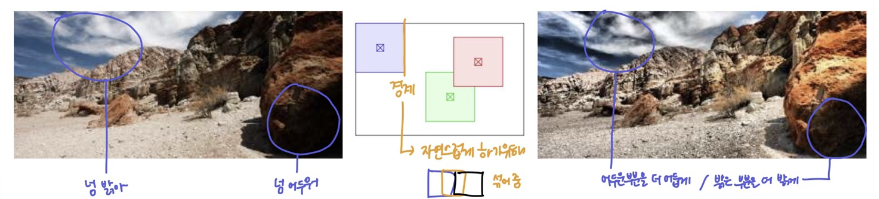
1-3. Composition & Matting
- 배경(background)에 전경(원하는 객체; foreground) 얹기
- alpha-matted color image
- 두 이미지를 합칠 떄 alpha값으로 조절 (위의 cross-dissolve)
- Over operator
- 이미지 전체가 아닌 픽셀마다 다른 alpha값을 주기
- C=(1-α)B+αF
- B: background, F: foreground
- 누끼따는 거는 α=1 (배경은 0, 전경이 1; 크로마키)
- Premultiplied
- png의 경우, RGB+alpha값으로 이뤄질 수 있는데, 매번 F에 곱하는 걸 덜 귀찮게하기 위해 미리 α곱하기 (안드로이드에서는 premultiplied 형태로 저장)

- Porter Duff operators
- C=(1-α)B+αF형태가 아닌 여러가지 조합 중 의미있는 조합을 나열해둔 것 (아래 표)
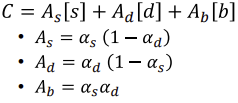
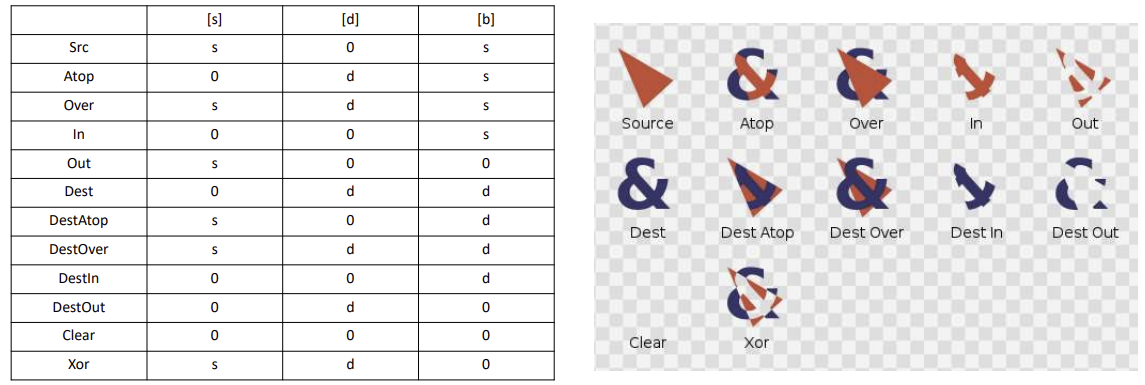
- C=(1-α)B+αF형태가 아닌 여러가지 조합 중 의미있는 조합을 나열해둔 것 (아래 표)
- alpha-matted color image
- Matting
- background와 foreground를 분리해서 추출, alpha matte(매팅)의 투명도 정보 얻어내기
- ex) 블루스크린
- 실제 이미지나 비디오에서 매팅 작업은 복잡함
2. Linear Neighborhood Operator
- neighborhood operator는 convolution 형태로 나타나는 filter
h를 사용하는 operator (요새는 lienar/nonlinear 둘 다 filter라고 함) - filter는 output pixel에 얼마나 영향을 줄지 결정하는 것
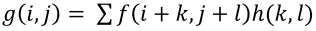
- Finite Impulse Response Filter (FIR Filter): k, l의 범위가 유한
-> 주어진 영역에 대해서만 적용되는 filter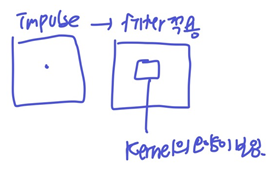
2-1. Cross-correlation filtering
- ex) mean filtering
- window (2k+1)(2k+1)영역의 평균
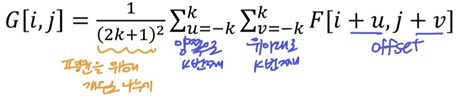
- window (2k+1)(2k+1)영역의 평균
- 1/(2k+1)^2를 시그마 안으로 넣고 H[u, v]라고 두면(Generalization)
-> 특정 픽셀에 어떤 값을 곱하고 더한 형태가 된다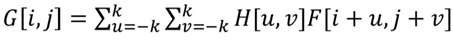
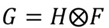
- 이것을 Convolution이라고 부른다.
- H: filter, kernel, or mask
Linear filtering as Convolution
- Convolution: 필터가 수직/수평으로 적용된 cross-correlation
- 각 픽셀끼리 곱한 것들 다 더함
(요새는 i+u, j+v도 convolution이라고 쳐준다..)- Symmetric kernels(상하좌우대칭): Gaussian, mean, Laplacian...
- Fourier transform으로 효율적으로 계산 가능
- k, l이 범위를 가지면 FIR필터
2-2. Mean(box) filtering
- 설명은 위에
- 주변과 방향성이 다른 노이즈를 지우기 위해 주변과 비슷하게 만들기 -> 평균
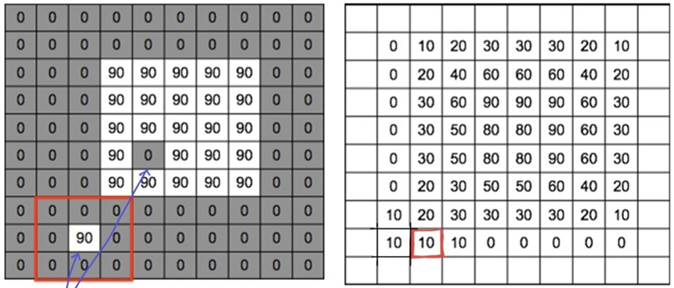
- mean kernel

2-3. Gaussian filtering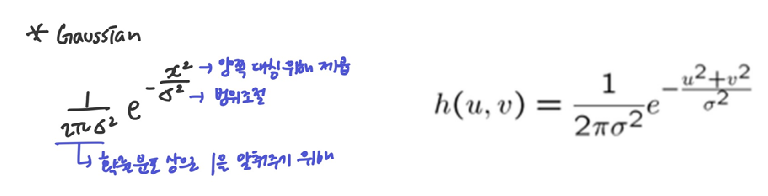
- Gaussian kernel
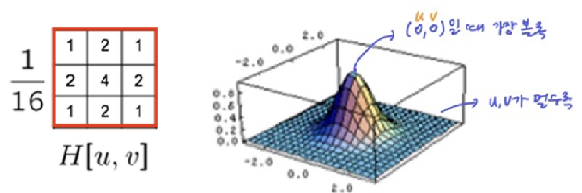
- 가우시안은 Low-pass filter(blur): reducing high-frequency noise
- High-pass filter: 원본
f- low frequencyh(blur)*f- Sharpening: high frequency 강조 ->
f+ 강조γ(f-h(blur)*f)
2-4. Padding
- 가장자리에 kernel이 없는 경우 이를 해결하는 방법

2-5. Sobel Filter
- sample 데이터 미분 -> 픽셀 값 차이를 미분 값으로 생각하는 discrete derivative (finite difference)
- mixed difference: right difference와 left difference를 합침
- f(x+1)-f(x) + f(x)-f(x-1) = f(x+1)-f(x-1)
- mixed difference에 한 축으로 만들어진 Gaussian을 적용 (노이즈를 줄이기 위해)
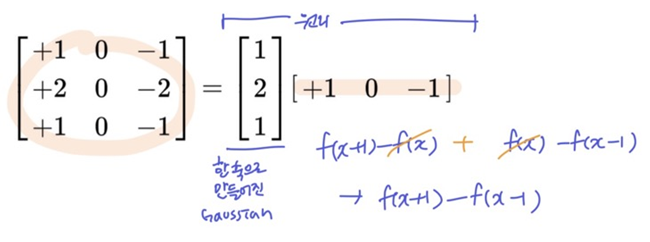
- x축 또는 y축으로 sobel

 -> 각 축의 방향에서 밝아지면 하얀색, 어두워지면 검정색
-> 각 축의 방향에서 밝아지면 하얀색, 어두워지면 검정색
-> 경계를 찾을 수 있다.
2-6. Image gradient
- x, y 미분 합치기 -> 벡터
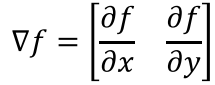
- 이미지가 밝아지는 방향과, 얼마나 밝아지는지 나타남

- Gradient direction (벡터 방향)
- 이미지가 밝아지는 방향
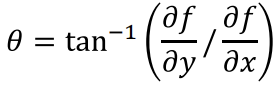
- 이미지가 밝아지는 방향
- Magnitude of gradient (벡터 길이)
- 이미지가 밝아지는 정도
- Edge에서 magnitude가 크다
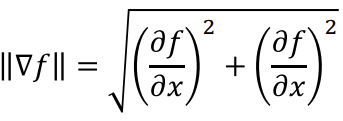

2-7. Directional(oriented) filter
- 위에서 x, y축으로 미분해서 변하는 정도를 알았는데, 내가 원하는 임의의 방향
u으로 얼마나 변하는가는 어떻게 알까 -> Directional derivative- Gradient field와 단위 방향 벡터
u간의 내적(dot product)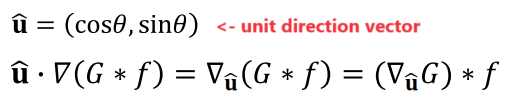
- 내적값은 단위 벡터 방향의 변화율
- 단위벡터 방향과 밝아지는 방향이 일치: 크기
- 단위벡터 방향과 밝아지는 방향이 수직: 0
- 단위벡터 방향과 밝아지는 방향이 반대: 음수
ex) 양수가 나왔다 -> (내가 궁금해한) 단위벡터로의 방향으로 이미지가 밝아지고있구나!
- Gradient field와 단위 방향 벡터
2-8. Steerable filter
- 특정 방향으로만 보는 필터 (ex 얼굴 주름살)
- 특정 방향으로만 convolutional filtering (필터링 할 방향 컨트롤 가능)
ex) Derivative of Gaussian- 특정 방향
u로만 Gaussian을 하고싶을 때 - motion blur
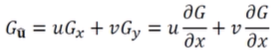
- 특정 방향
2-9. Laplacian
- 두번 미분 (x 두번 미분 + y 두번 미분) -> undirectied
- 자신과 주변이 얼마나 다른지 (
상하좌우의 합-자신의 4배)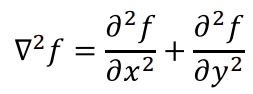
- LoG (Laplacian of Gaussian)
- noise를 없애기 위해 또는 원하는 주파수 영역만 남겨두기 위해 smoothing 한 뒤 Laplacian
- Gaussian 정도에 따라 다른 결과

2-10. Band-pass filter (= Difference of Gaussian(DoG))
- low, high가 아닌 중간 frequency만 pass
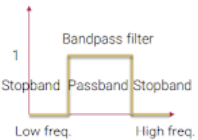
- Difference of Gaussian(DoG)로 중간 frequency만 구할 수 있다
- DoG: 다른 크기의 가우시안 필터의 차이 (작은 표준 편차와 큰 표준 편차의 차이)
- 표준편차 작음
σ1: 좁고 뾰족; 높은 주파수 약간만 사라짐 (거의 middle~low frequency) - 표준편차 큼
σ2: 넓고 평평; 높은 주파수 많이 사라짐 (거의 low frequency만 남음)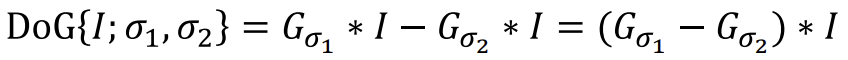 (Symmetric하기 때문에 가우시안의 차이 계산 후 I에 convolution하기 가능)
(Symmetric하기 때문에 가우시안의 차이 계산 후 I에 convolution하기 가능)
- Laplacain of Gaussian version
- DoG한 뒤 Laplacian 적용
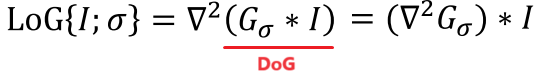
- DoG한 뒤 Laplacian 적용
Typical Operators
- box(moving average, mean)
- bilinear (3x3)
- Gaussian
- Sobel
- Laplacian
Up-sampling
- 해상도를 늘리는 영상처리 연산
- 이미지의 크기를 확대
Interpolation
- 누락된 픽셀값 예측, 대체
h: interpolation kernelr: 배율 (이미지를 r배로 키운다)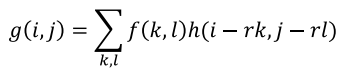
- bilienar: 두 점 사이를 직선으로 이어서 예측(두 픽셀 사이의 값이 선형적일 것이라고 예측)
- bicubic: 네 점 사이를 삼차함수를 사용해 곡선으로 이어서 예측
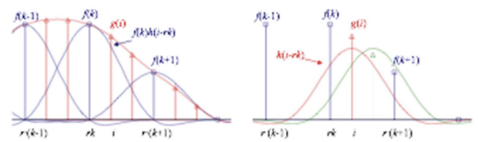 (파란점이 원본이고, 빨간점이 예측한 값)
(파란점이 원본이고, 빨간점이 예측한 값) (b: bilinear, c: bicubic)
(b: bilinear, c: bicubic)bi가 붙는 이유는 아래 이미지는 한 축만 고려한 것이고, 실제 이미지(2차원)에서는 x, y 두 축을 고려해야하므로 lienar/cubic 방법을 2번하므로- 그래서 실제로는 bilienar는 총 4개의 점이, bicubic은 총 16개의 점이 필요하다
Down-sampling (Decimation)
- 해상도를 줄이는 영상처리 연산
- 이미지의 크기를 축소
Low-pass filtering & re-sampling
- interpolation kernel을 사용
주변 픽셀들의 선형적인 예측을 할 때, 한 픽셀의 값이 변할 때 받는 영향의 정도를 픽셀값에 따라 정함?- a의 빨간 곡선의 주기만큼 sampling할 때, 곡선을 따라서 기존 픽셀들의 영향의 정도를 결정한다. (빨간 곡선이 높은 곳의 픽셀의 가중치가 가장 높도록하여 주변 픽셀들과
선형적으로예측) - down-sampling한다고 중간 픽셀들을 그냥 삭제해버리면 부자연스러워지므로 위와같은 방법을 사용하는 것이다.
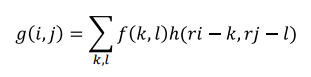
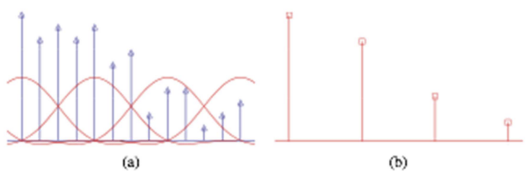 (b의 원본 빨간값에 a의 빨간함수를 곱해서 파란값을 얻는건 up-sampling이고 반대로해서 a의 값과 비슷하게 만드는 과정이 down-sampling)
(b의 원본 빨간값에 a의 빨간함수를 곱해서 파란값을 얻는건 up-sampling이고 반대로해서 a의 값과 비슷하게 만드는 과정이 down-sampling)
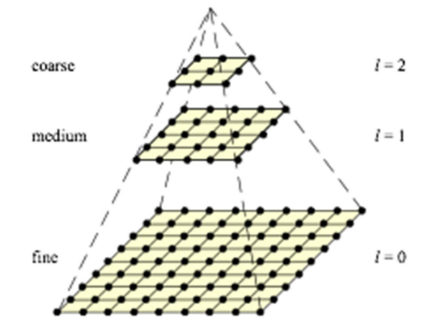
Image Pyramid(Multi-resolution representation)
- 다양한 해상도의 이미지, 각각 다른 정보들을 가진다.
- 해상도가 낮을수록 대략적인 정보를 가지고, 다루기 쉽다.
- Scale-invariant feature detection
- 스케일 불변 특징 검출 (ex 얼굴 인식)
- 특징을 대략적으로 찾은뒤, 이를 기반으로 이미지간의 matching 수행
- Multi-band blending
과제- edge를 보존하면서 부드럽게 연결
- Laplacian pyramid 사용
Gaussian Pyramid
- Gaussian을 하고 Downsampling
- 계속 low-pass로 쌓아 나감 (high를 차근차근 날려버림)
Gaussian filter를 사용해서 크기 조절
Find to coarse
- 고해상도->저해상도 (down-sampling)
가우시안 블러처리 후 짝수행과 열을 제거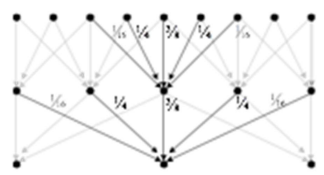
Coarse to find
- 저해상도->고해상도 (up-sampling)
짝수행과 열에 zero pixel을 추가한 후 가우시안 블러처리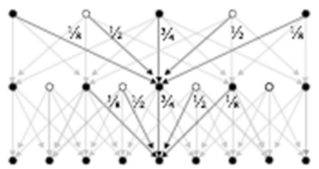
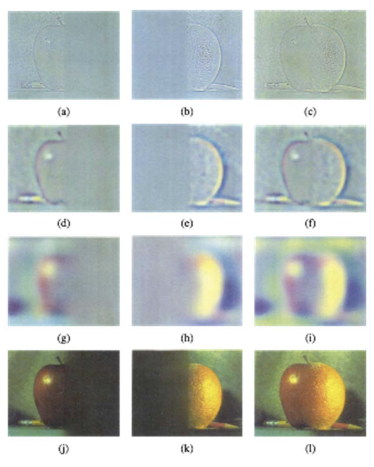
Laplacian Pyramid
- 원본 이미지와 Gaussian pyramid의 이전 단계 이미지를 2배(크기만 키움; low frequency)의 차이
- 위의 차이는 Gaussian pyramid에서 down-sampling을 하면서 사라진 것을 나타내기도 한다.
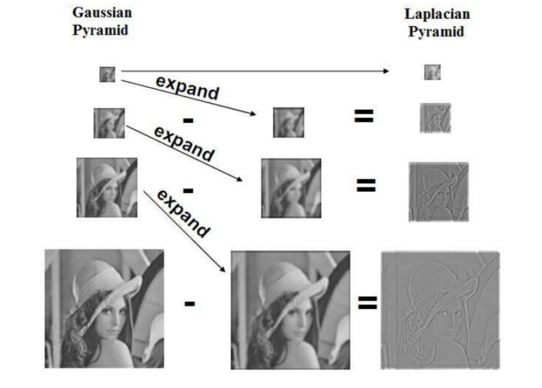
- 차이들을 나열하다보면 처음에는 high frequency, 중간에는 band-pass image들, 마지막에는 굉장한 low frequency의 이미지만 남는다.
- Lowest octave
L(l) = G(l; f)(걍 이미지에 Gaussian한 값) - Higher octave
L(l) = G(l; f) - Upsampling(G(l+1; f))( 전단계 꺼 upsampling해서 뺀 거)
- Lowest octave
- Finest octave: high pass
- Middle octaves: band pass
- Lowest octave: low pass
- a, b, c -> high frequency; Fattening? 거의 없게 칼같이 반 자름 (디테일 한 것은 옆으로 번저나가지 않도록, ghosting 현상 방지)
- d, e, f -> middle frequency; Fattening 약간넣어서 부드럽게 자름
- g, h, i -> low frequency; Fattening 많이 넣어서 흐릿하게 자름

❗ Gaussian pyramid는 Low-pass반복하기 때문에 Low freq의 이미지들의 나열, Laplacian pyramid는 high freq + middle freq의 나열 + low freq이다.
3. Nonlinear Neighborhood Operator
Non-linear Filtering
- 이웃픽셀의 비선형 조합으로 outlier에 민감한 걸 보완
- Median filtering(노이즈 , α-trimmed mean(가장자리 제외하고 평균), weighted median
3-1. Bilateral filtering
- 거리가 너무 멀고, 색도 너무 다르면 weight를 적게 준다.
- edge를 유지하며 blur
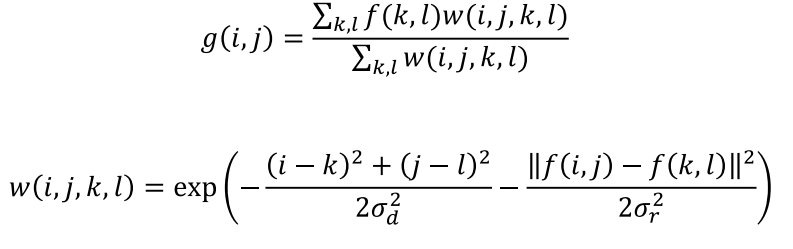 -> exp(위치(거리)에 따른 가우시안과 픽셀값에 따른 가우시안의 차이)
-> exp(위치(거리)에 따른 가우시안과 픽셀값에 따른 가우시안의 차이)
- Bilateral filter kernel
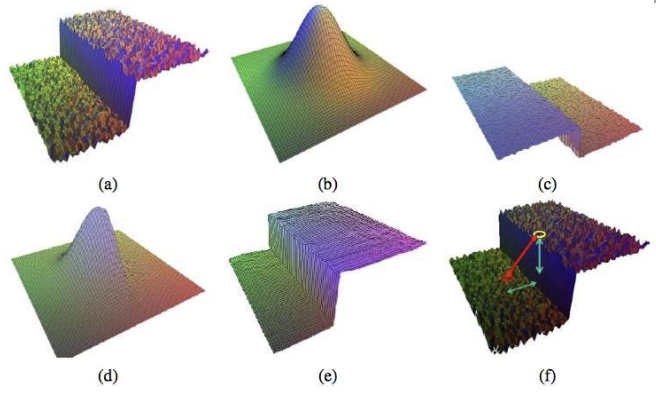
- 원본 a에서 특정 픽셀을 기준으로 픽셀 값에 따른 정도를 나타낸게 c
- b와 c를 곱해서 비슷한 색일수록 가우시안 형태인 d를 만듦
- 모든 픽셀에 대해 구한 뒤, filtering하여 edge가 유지되며 blur된 e를 구함
(너무 느리고, 시그마 두개를 주는게 어려워서 자주 안 쓰임)
3-2. Morphology
- c: 범위(보통 3x3) 내에서 1로 설정된 픽셀의 개수
- 범위 내에 있는 픽셀의 수 (3x3=9)
- dilation: c>0 (범위 내에 1이 하나라도 있으면 해당 픽셀 1)
- erosion: c>=S (범위 내에 모든 픽셀이 1이면 해당 픽셀 1)
- majority: c>S/2 (범위 내에 1인 픽셀이 절반 이상이면 해당 픽셀 1)
- opening: dilate(erode())
- closing: erode(dilate())
Distance transforms
- 특정 점
(k, l)기준으로 각 점마다 거리 중 min(얼마나 가까운가) - 이미지 상의 각 픽셀에서 가장 가까이 놓인 물체(전경)의 경계까지 거리를 구하는 연산 (배경 픽셀에서 전경까지의 거리)
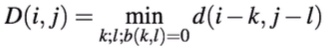
- manhattan (x, y 거리 합침) / Euclidean (x, y 제곱의 합 루트)
Connected Component
- 연결된 픽셀들 찾기
- 자신과 동일한 값을 가지는 인접한 픽셀의 범위
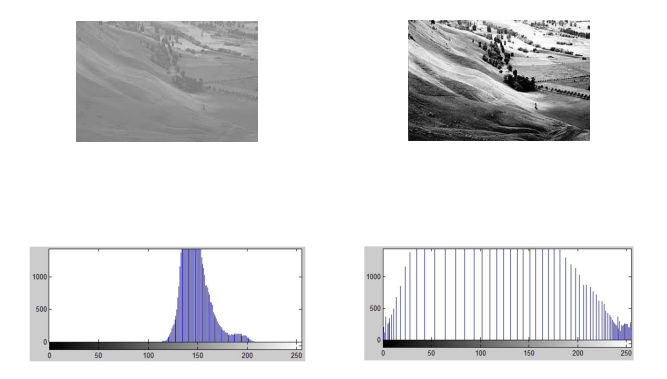
3-3. Histogram Equalization
- constrast가 낮을 때 사용
- 히스토그램(누적도수분포)의 합인 누적도수분포 가 직선이 되도록하는 intensity mapping function
(히스토그램이 평탄하면 누적도수분포가 직선에 가까워지므로) - 자기보다 어두운 픽셀의 비율 을 따져서 조절하여 평탄화를 할 수 있다.
ex)
자기보다 어두운 픽셀이 없으면 -> 자신의 밝기 0로 조절
자기보다 어두운 픽셀이 50%면 -> 자신의 밝기를 0.5로 조절
전부 자기보다 어두운 픽셀이면 -> 자신의 밝기를 1로 조절
- Partial compensation: 대비 개선을 위해 다른 영역으로 보상
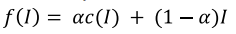
Local adaptive histogram equalization
- 지역적으로 적응형 히스토그램 평활화 수행
- 이미지를 분할시켜서 구역 내에서 히스토그램을 계산
- 구역마다의 경계선이 부자연스러울 수 있으므로 보간하여 부드럽게 연결