#2805 나무자르기

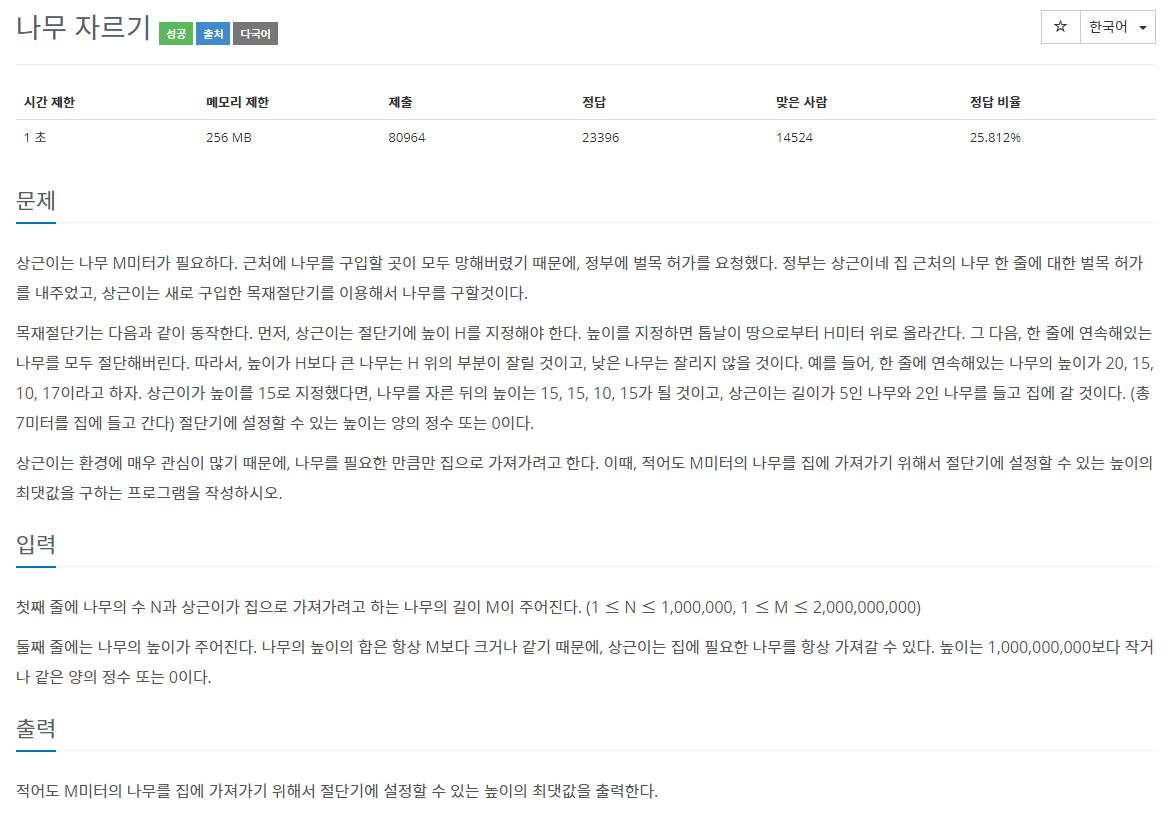
교재에 있던 떡볶이 떡 만들기를 학습한 후 유사하게 풀었는데 시간 초과가 떴습니다 ㅜ.ㅜ

시간초과 코드

import sys

n,m=map(int,sys.stdin.readline().split())
tree=list(map(int,sys.stdin.readline().split()))

start = 0
end = max(tree)

result = 0

while(start<=end):
    total=0
    mid=(start+end)//2
    for i in tree:
        if i>mid:
            total+=i-mid
    
    if total<m:
        end=mid-1
    else:
        result=mid
        start=mid+1
    
print(result)

질문 검색을 통해 여러 사례를 보니
(파이썬의 경우) 단순 반복문을 함수로 따로 구현하면 시간초과가 안난다는 글을 보고
그렇게 구현했더니 성공했어요.

성공한 코드

import sys

n,m=map(int,sys.stdin.readline().split())
tree=list(map(int,sys.stdin.readline().split()))

#이진탐색 함수
def binary_search(target,start,end):
    result=0
    while(start<=end):
        total=0
        #중간 값 설정
        mid=(start+end)//2
        
        #기준 길이(mid)로 잘랐을 경우 총 몇미터가 나오는지 구하기 위함
        #tree를 모두 돌아가며 기존 tree에서 기준 길이(mid)를 자른 값을 더해준다
        for i in tree:
            if i>mid:
                total+=i-mid
                
        #모두 더해준 값이 target보다 작다면 범위를 왼/오로 나눴을 때 왼쪽으로 범위 다시 수정
        if total<target:
            end=mid-1
        #아닐 경우 범위를 오른쪽으로 다시 수정 -> 최댓값을 구하는 과정!
        else:
            result=mid
            start=mid+1
    return result
    
print(binary_search(m,0,max(tree)))

성공한 이유?
https://stackoverflow.com/questions/11241523/why-does-python-code-run-faster-in-a-function
파이썬 시스템의 내부적인 문제
그냥 그렇게 설계된 듯 합니다...
이 문제를 통해 웬만하면 함수로 구현해 푸는것이 빠르다는걸 알게되었습니다!

#1654 랜선자르기

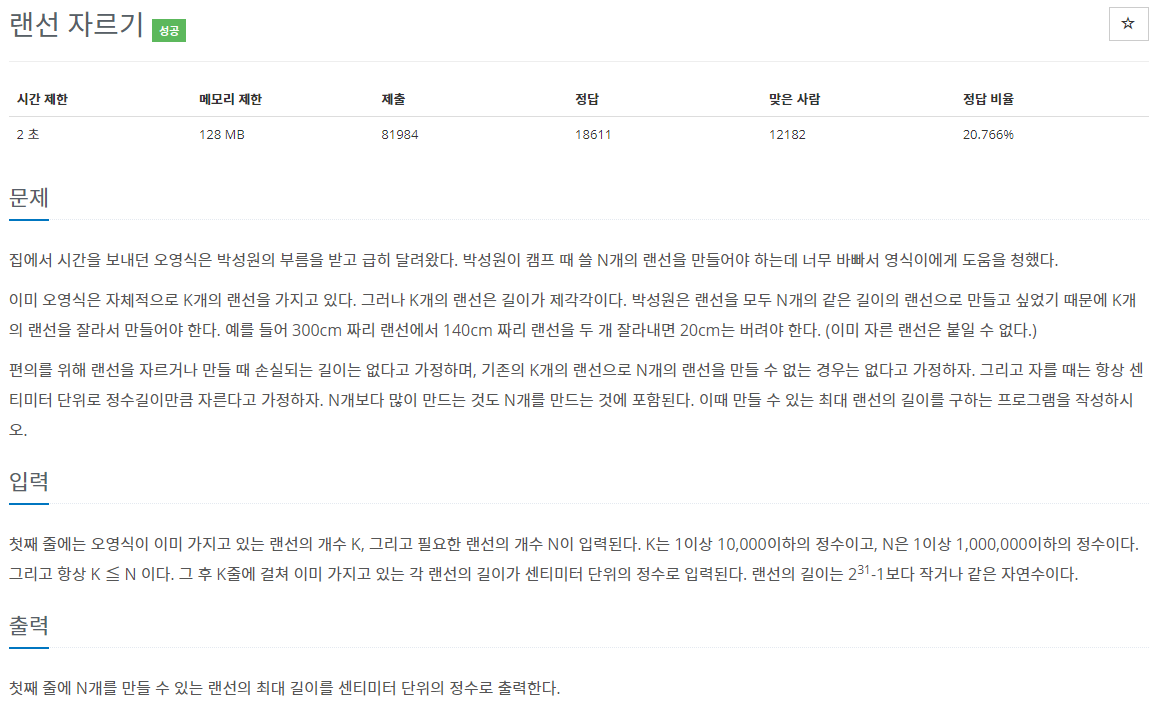
위의 문제(나무자르기)와 비슷한 구조라 이번에는 재귀함수로 구현해보았습니다!

성공한 코드

import sys

k,n=map(int,sys.stdin.readline().split())
lan=[int(sys.stdin.readline().rstrip()) for _ in range(k)]

def binary_search(target,start,end):
    global result
    if start>end:
        return None
    total=0
    #중간 값 설정
    mid=(start+end)//2
    
    #기준 길이(mid)로 잘랐을 경우 총 몇개가 나오는지 구하기 위함
    #lan을 모두 돌아가며 기존 lan에서 기준길이(mid)를 나눈 몫을 더해준다.
    for i in lan:
        total+=(i//mid)

    #모두 더해준 값이 target보다 작다면 범위를 왼/오로 나눴을 때 왼쪽으로 범위 다시 수정
    if total<target:
        return binary_search(target,start,mid-1)
    #아닐 경우 범위를 오른쪽으로 다시 수정 -> 최댓값을 구하는 과정!
    else:
        result=mid
        return binary_search(target,mid+1,end)

binary_search(n,1,max(lan))
print(result)

#10816 숫자카드 2

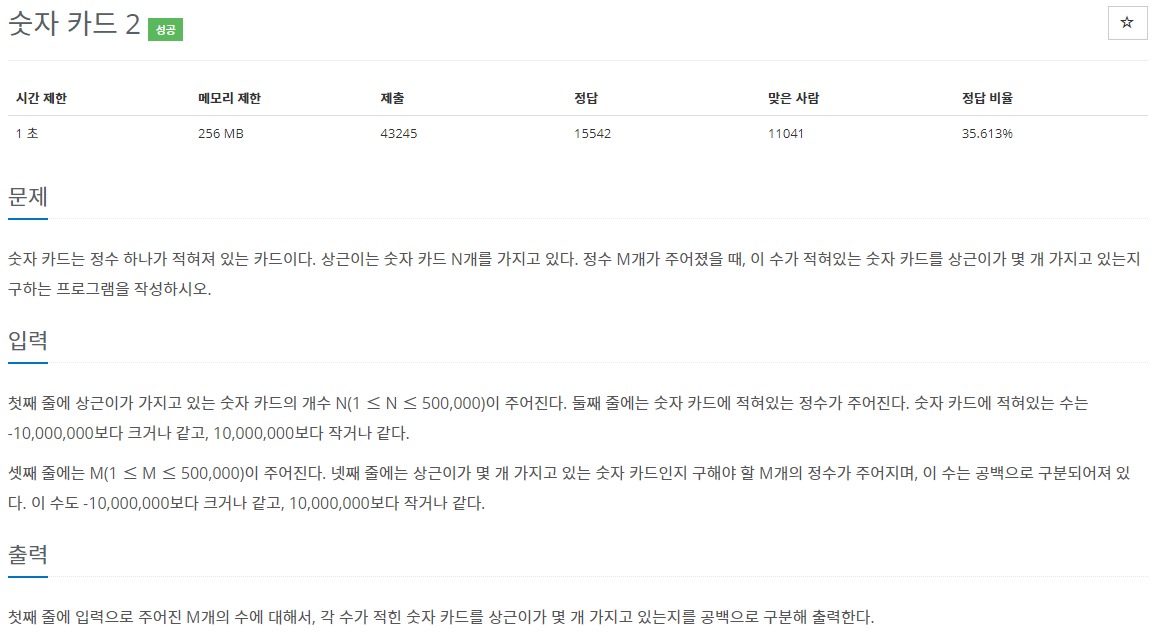
교재에 있는 부품찾기 문제와 유사하다고 느껴졌어요! 근데 중복 숫자를 다뤄줘야하는..
딕셔너리를 통해 한번 싹 도는게 확실히 효율적일 것 같은데 최대한 이진 탐색으로 풀어보려고 했어요.

처음 시도 (시간초과로 실패ㅠ.ㅠ)

시간초과 코드

import sys

#부품찾기 문제와 비슷하다!

def binary_search(target,start,end):
    global cnt
    cnt=0
    while start<=end:
        mid=(start+end)//2
        if sang[mid]==target:
            cnt+=1
            for i in range(1,mid-start+1):
                if sang[mid-i]!=sang[mid]:
                    break
                else:
                    cnt+=1
            for i in range(1,end-mid+1):
                if sang[mid+i]!=sang[mid]:
                    break
                else:
                    cnt+=1
            return None       
        elif sang[mid]>target:
            end=mid-1
        else:
            start=mid+1

n = int(sys.stdin.readline().rstrip())
sang=list(map(int, sys.stdin.readline().split()))
m = int(sys.stdin.readline().rstrip())
num=list(map(int, sys.stdin.readline().split()))
solution=[]

#이진탐색을 위해 정렬한다
sang.sort()

for i in num:
    binary_search(i,0,n-1)
    solution.append(cnt)

for i in solution:
    print(i, end=' ')

문제되는 코드는 이 부분(으로 예상)

        if sang[mid]==target:
            cnt+=1
            for i in range(1,mid-start+1):
                if sang[mid-i]!=sang[mid]:
                    break
                else:
                    cnt+=1
            for i in range(1,end-mid+1):
                if sang[mid+i]!=sang[mid]:
                    break
                else:
                    cnt+=1
            return None

중복인 숫자카드를 다뤄주기 위해
target의 숫자와 같은 카드를 발견할 경우,
해당 숫자 앞뒤로 한번씩 리스트를 돌면서 같은 숫자가 있는지 확인을 해주려고 했는데
이게 최악일 경우 (해당 리스트가 다 같은 숫자일 경우)
엄청나게 반복문을 돌게됩니다.

이후 백준에서 질문 검색을 했는데,
lower bound & upper bound 를 이용해 풀었다는 글을 봐서 검색을 해보니

lower bound : 찾고자 하는 값보다 이상인 값이 처음 나타나는 위치 찾기
upper bound : 찾고자 하는 값보다 초과된 값이 처음 나타나는 위치 찾기

라고 이해할 수 있었으며, 이것들 모두 이진탐색을 활용해 구현하더라구요.

아 그러면 두 번의 이진탐색을 통해 찾는 숫자의 최소 인덱스, 최대 인덱스를 찾은 다음에
(최대 인덱스 - 최소 인덱스)를 해 해당 숫자의 갯수를 세면 되겠구나! 하고 다시 구현했습니다.

성공한 코드 (PyPy로만 성공했어요...)

import sys

#부품찾기 문제와 비슷하다!

#찾고자하는 값이 가장 처음 나타나는 위치 탐색 (lower bound)
def lower_binary_search(target,start,end):
    while start<=end:
        mid=(start+end)//2 
        #target과 "같거나" 큰 숫자를 만났을 때 범위를 왼쪽으로 줄임으로써 해당 숫자를 가진 최소의 인덱스를 구함!
        if sang[mid]>=target:
            end=mid-1
        else:
            start=mid+1
    return start
    
#찾고자하는 값보다 큰 값이 가장 처음에 나타나는 위치 탐색 (upper bound)
def upper_binary_search(target,start,end):
    while start<=end:
        mid=(start+end)//2 
        if sang[mid]>target:
            end=mid-1
        #target과 "같거나" 작은 숫자를 만났을 때 범위를 오른쪽으로 줄임으로써 해당 숫자를 가진 최대의 인덱스를 구함!
        else:
            start=mid+1
    return start

n = int(sys.stdin.readline().rstrip())
sang=list(map(int, sys.stdin.readline().split()))
m = int(sys.stdin.readline().rstrip())
num=list(map(int, sys.stdin.readline().split()))

#이진탐색 위해 정렬한다
sang.sort()

for i in range(m):
    #범위 계산 후 출력
    print(upper_binary_search(num[i],0,n-1)-lower_binary_search(num[i],0,n-1),end=' ')

Python3에서는 여전히 시간초과가 뜨는데
이 이상 이진탐색으로 효율적인 방법을 구하는게 어려워서 넘어가기로 하였습니다 ㅠ

#2110 공유기 설치

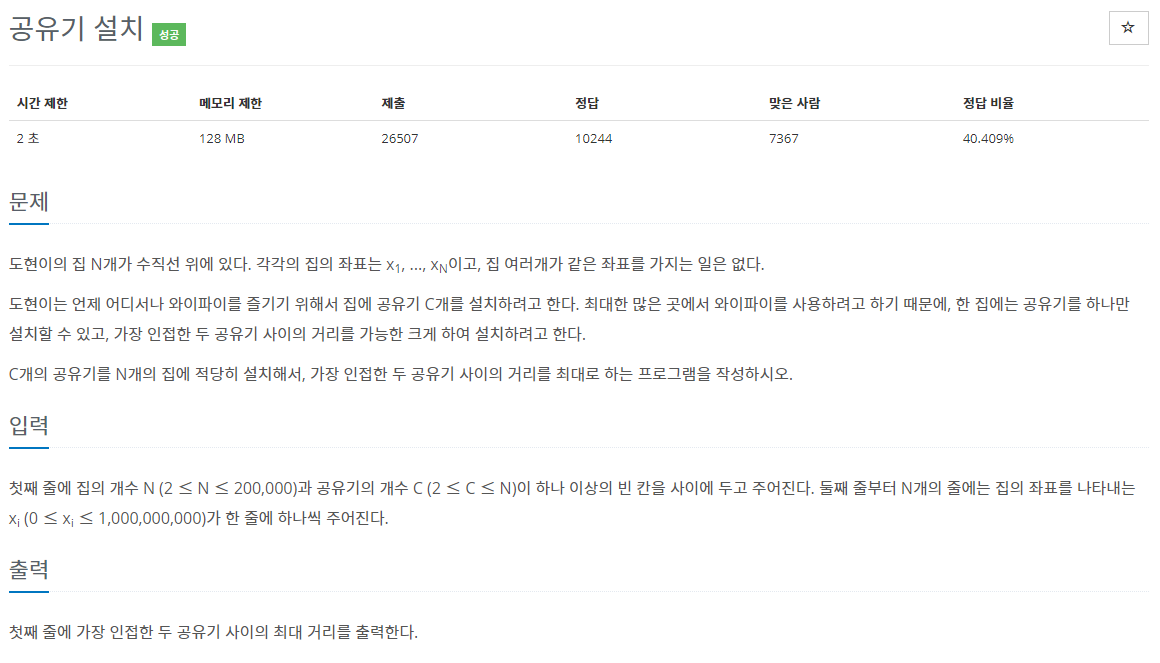
여기서 잠깐 멈칫했는데, 도대체 이걸 이진탐색으로 어떻게 풀어야하는지 잘 감이 안 왔어요. 그래서 정리한게

1. 내가 무엇을 구해야하는지 확인하기!
   이 문제에서는 가장 인접한 두 공유기 사이의 최대 거리
   ->이진 탐색을 할 때의 범위(start, end)를 정하는데 기준이 됨
2. 1번을 구해야하는데 필요한 기준 확인하기
   이 문제에서는 공유기의 개수
   ->이진 탐색을 할 때 쓰는 기준(target)이 됨

위 두가지를 섞어서
(start+end)//2의 거리일 때 필요한 공유기의 개수를 찾고.
이 개수가 target의 개수보다 큰지 작은지 비교해 범위를 좁혀나가며 위 과정을 반복해 그 중 가장 최대의 거리를 찾았습니다!

성공한 코드

import sys

n,c=map(int,sys.stdin.readline().split())
house = [int(sys.stdin.readline().rstrip()) for _ in range(n)]

#이진 탐색
def binary_search(start,end,target):
    result=0
    while(start<=end):
        mid=(start+end)//2
        
        #해당 거리(mid)를 사이에 두고 공유기를 설치한다했을때
        #몇개의 공유기를 설치할 수 있는가 셉니다
        cnt=1
        tmp=house[0]
        for i in range(1,n):
            if mid+tmp<=house[i]:
                cnt+=1
                tmp=house[i]
        
        #target(설치해야하는 공유기 개수)와 비교
        if cnt<target: #공유기가 더 적게 설치될경우
            end=mid-1 #공유기 사이의 거리가 너무 큰 것이므로 범위를 왼쪽으로 좁힘
        else: #공유기가 더 많이(혹은 같게) 설치될 경우 -> 거리의 최댓값을 구하는 과정! 
            result=mid #공유기 사이의 거리가 너무 작거나 같은 것이므로 범위를 오른쪽으로 좁힘
            start=mid+1

    return result

#이진 탐색을 위한 정렬
house.sort()
#차례대로 (공유기 사이에 나올 수 있는 거리의) 최소값, 최대값, 그리고 공유기의 개수
print(binary_search(1,house[-1]-house[0],c))

#3079 입국심사

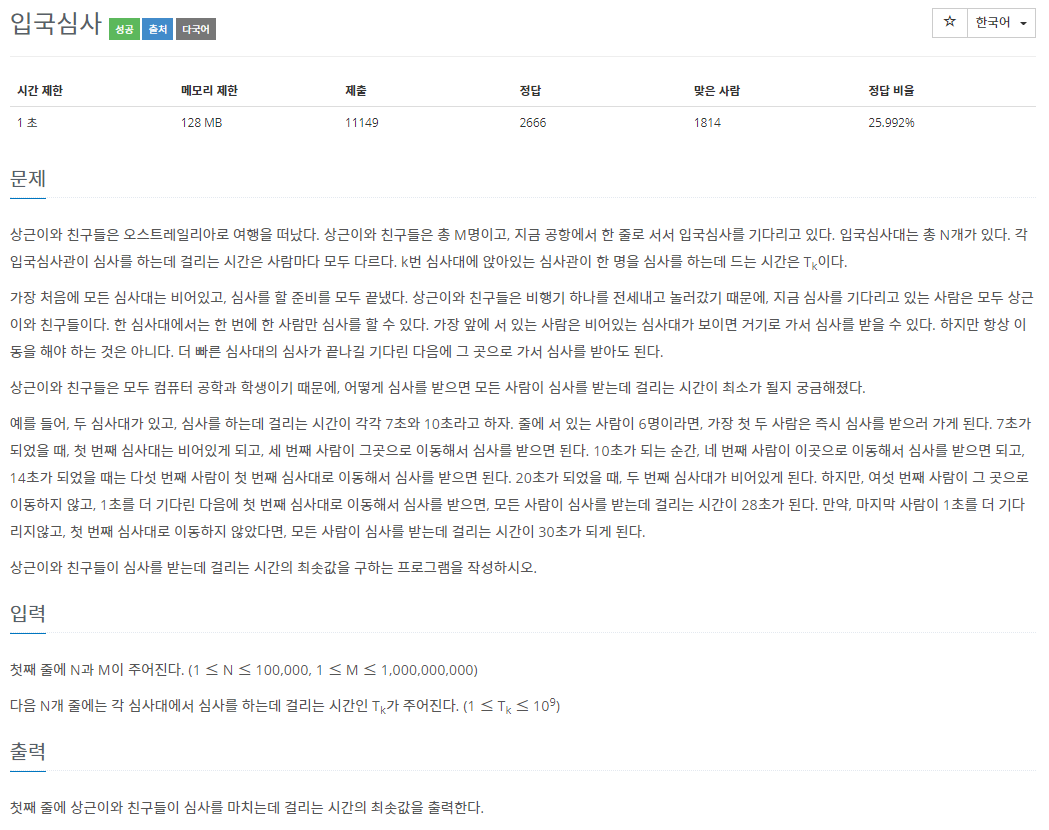
위의 문제(공유기 설치)와 똑같이 풀었습니다!

1. 내가 무엇을 구해야하는지 확인하기!
   이 문제에서는 심사를 마치는데 걸리는 시간의 최솟값
   ->이진 탐색을 할 때의 범위(start, end)를 정하는데 기준이 됨
2. 1번을 구해야하는데 필요한 기준 확인하기
   이 문제에서는 상근이와 친구들의 인원 수
   ->이진 탐색을 할 때 쓰는 기준(target)이 됨

성공한 코드

import sys

n,m =map(int,sys.stdin.readline().split())
immi = [int(sys.stdin.readline().rstrip()) for _ in range(n)]

#이진탐색
def binary_search(start,end,target):
    result=0
    while(start<=end):
        mid=(start+end)//2

        #해당 시간 만큼 입국 심사를 한다 했을 때 몇 명을 심사할 수 있는가 셉니다
        cnt=0
        for i in immi:
            cnt+=(mid//i)

        #target(심사해야하는 사람 수)와 비교
        if cnt<target: #더 적은 사람을 심사할경우
            start=mid+1 #시간이 너무 짧은 것이므로 범위를 오른쪽으로 좁힘
        else: #더 많은 사람(혹은 같은)을 심사하는 경우 -> 시간의 최솟값을 구하는 과정!
            result=mid #시간이 너무 길거나 같은 것이므로 범위를 왼쪽으로 좁힘
            end=mid-1
    return result

#이진 탐색을 위한 정렬
immi.sort()
#차례대로 (심사를 마치는데 필요한 시간의) 최솟값, 최댓값, 그리고 심사해는 사람의 명수
print(binary_search(1,max(immi)*m,m))