
1️⃣ 문제 설명
△△ 게임대회가 개최되었습니다. 이 대회는 N명이 참가하고, 토너먼트 형식으로 진행됩니다. N명의 참가자는 각각 1부터 N번을 차례대로 배정받습니다. 그리고, 1번↔2번, 3번↔4번, ... , N-1번↔N번의 참가자끼리 게임을 진행합니다. 각 게임에서 이긴 사람은 다음 라운드에 진출할 수 있습니다. 이때, 다음 라운드에 진출할 참가자의 번호는 다시 1번부터 N/2번을 차례대로 배정받습니다. 만약 1번↔2번 끼리 겨루는 게임에서 2번이 승리했다면 다음 라운드에서 1번을 부여받고, 3번↔4번에서 겨루는 게임에서 3번이 승리했다면 다음 라운드에서 2번을 부여받게 됩니다. 게임은 최종 한 명이 남을 때까지 진행됩니다.
이때, 처음 라운드에서 A번을 가진 참가자는 경쟁자로 생각하는 B번 참가자와 몇 번째 라운드에서 만나는지 궁금해졌습니다. 게임 참가자 수 N, 참가자 번호 A, 경쟁자 번호 B가 함수 solution의 매개변수로 주어질 때, 처음 라운드에서 A번을 가진 참가자는 경쟁자로 생각하는 B번 참가자와 몇 번째 라운드에서 만나는지 return 하는 solution 함수를 완성해 주세요. 단, A번 참가자와 B번 참가자는 서로 붙게 되기 전까지 항상 이긴다고 가정합니다.
2️⃣ 제한 사항
- N : 21 이상 220 이하인 자연수 (2의 지수 승으로 주어지므로 부전승은 발생하지 않습니다.)
- A, B : N 이하인 자연수 (단, A ≠ B 입니다.)
3️⃣ 입출력 예
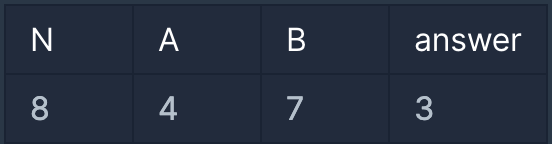
4️⃣ 나의 풀이
function solution(n,a,b)
{
let cnt = 1;
while(Math.ceil(a/2)!==Math.ceil(b/2)){
a = Math.ceil(a/2);
b = Math.ceil(b/2);
cnt++;
}
return cnt;
}
1-2번,3-4번참가자가 붙게 된다.
--> 2로 나누어 떨어지는 값의 n-1번째 값과 만나게 되는 것이므로Math.ceil()을 이용하여 올림을 해줬다.
a와 b가 붙게 되는 순간 === 같은 번호로 한 쌍이 되는 순간까지 라운드를 진행
cnt를 증가시키면서 같은 번호가 될 때 반복문 종료
return count
