[LeetCode] Minimum Time Visiting All Points

1.문제

On a 2D plane, there are n points with integer coordinates points[i] = [xi, yi]. Return the minimum time in seconds to visit all the points in the order given by points.

You can move according to these rules:

• In 1 second, you can either:
  • move vertically by one unit,
  • move horizontally by one unit, or
  • move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in 1 second).
• You have to visit the points in the same order as they appear in the array.
• You are allowed to pass through points that appear later in the order, but these do not count as visits.

평면에 방문해야하는 점들의 x,y좌표값을 2차원 배열 points로 주어진다고 할 때

1초에 다음과 같이 이동할 수 있다고 한다

• 수직방향으로 1칸
• 수평방향으로 1칸
• 대각 방향으로 sqrt(2) 칸 (수직 한칸, 수평 한칸)

이러한 조건에서 모든 점을 방문하는데 소요되는 최소 시간을 구하는 문제이다.

Example 1

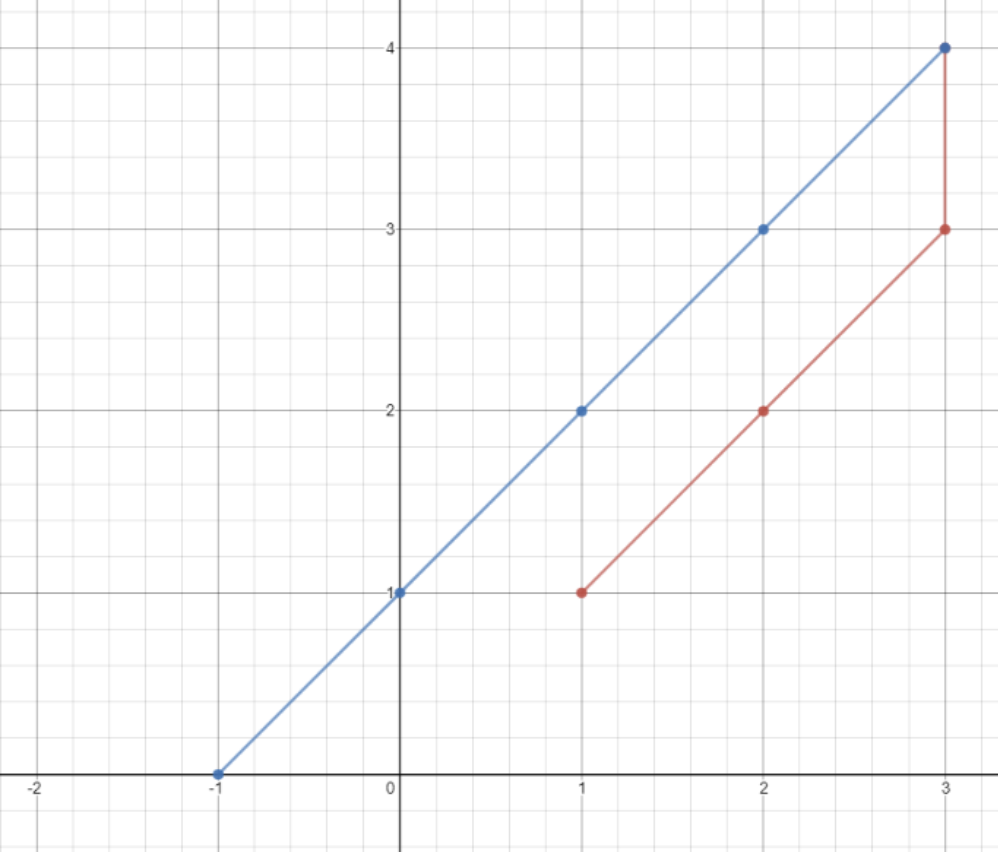
Input: points = [[1,1],[3,4],[-1,0]]
Output: 7
Explanation: One optimal path is [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]   
Time from [1,1] to [3,4] = 3 seconds 
Time from [3,4] to [-1,0] = 4 seconds
Total time = 7 seconds

Example 2

Input: points = [[3,2],[-2,2]]
Output: 5

Constraints:

• points.length == n
• 1 <= n <= 100
• points[i].length == 2
• -1000 <= points[i][0], points[i][1] <= 1000

2.풀이

1. 현재 점에서 다른 점까지 이동하는데 걸리는 최소시간은 x,y 좌표간의 차이중 절댓값이 가장 큰 값이다.

/**
 * @param {number[][]} points
 * @return {number}
 */
const minTimeToVisitAllPoints = function (points) {
  let count = 0;

  for (let i = 0; i < points.length - 1; i++) {
    // 현재 점에서 다음 점 사이 x,y 좌표 값의 차이의 절댓값중 큰 값이 다음 점으로 이동하는데 걸리는 시간이다.
    count += Math.max(
      Math.abs(points[i][0] - points[i + 1][0]),
      Math.abs(points[i][1] - points[i + 1][1])
    );
  }

  return count;
};

3.결과