성균관대학교 블록체인 네트워크 SKKRYPTO에서 연재한 글을 학회 블로그에만 두고 제 블로그에 안 쓰기는 너무 아까워서 가져옵니다. 문제시 회장님 연락주세요 ㅎㅎ;
**포스팅에 이미지가 너무 많아서 다시 올리겠습니다. 데모버전입니다.
블록체인이 궁금하다면? SKKRYPTO 브런치
출처 : Programming Bitcoin by Jimmy Song(O'Reilly). Copyright 2019 Jummy Song, 978-1-492-03149-9
안녕하세요, 스크립토 5기 배준호입니다. 지난 챕터에서 유한체를 다루었고, 이번 챕터에서는 타원곡선을 다룰 것입니다. 사실 유한체와 타원곡선은 '타원곡선 암호'를 사용하기 위한 도구라고 생각하면 됩니다. 타원곡선 암호는 비트코인에서 사용하는 서명과 검증 알고리즘의 핵심이기 때문에 조금 자세하게 다루어 보려고 합니다. 타원곡선 자체는 중고등학교 수준의 수학적 지식이 있으면 충분히 이해할 수 있기 때문에 큰 부담은 없을 것 같습니다. 하지만 개인적으로는 타원곡선 암호 부분이 조금 어려웠는데, 이 부분을 정확하게 이해하기 위해서는 유한체와 타원곡선의 속성을 명확하게 알고 있어야 합니다.
Chapter 2. 타원곡선
타원곡선은 말 그대로 수학시간에 다루었던 타원곡선을 구현하면 됩니다. 다만, 지금까지 다루었던 유한체가 타워곡선에 적용된다는 점이 다를 뿐입니다. 이를 통해서, 후에 타원곡선 암호를 다룰 수 있고, 타원곡선 암호를 통해서 개인키와 공개키 생성 알고리즘을 다룰 수 있습니다. 수 많은 타원곡선 중에서도, 우리가 다룰 타원곡선은 아래의 모습과 같습니다. 어렵게 생각할 것 없이, 그냥 함수이고 곡선입니다.
secp256k1 타원곡선
1. 타원곡선의 정의
y^2=x^3+ax+b
타원곡선은 위와 같은 식으로 정의됩니다. 이런 수 많은 타원 곡선 중에서, 특히 비트코인에서 채택한 타원곡선은 secp256k1이라고 합니다. 이는 a=0, b=7인 비교적 간단한 형태입니다. 즉, 아래와 같은 형태의 타원 곡선을 사용하는 것입니다. 그리고 모양은 바로 위의 그림과 같습니다.
사실 타원곡선을 파이썬으로 다루는 것은 어렵지 않습니다. 위의 방정식을 그대로 클래스로 구현을 해서, 값을 받아 초기화 시킬 때 마다 생성자에서 조건을 고려하기만 하면 된다. 우리가 원하는 secp256k1 곡선은 파라미터 a를 0, b를 7로 넘기면서 생성하면 됩니다. 코드로는 곡선 위의 각각의 점을 구현합니다.
타원곡선함수 위의 점
코드분석
곡선 위의 점을 구현한 Point 클래스입니다.
1) a,b는 계수를 의미하고, x,y는 점의 x좌표와 y좌표를 의미합니다. 생성자에서 패러미터로 각각의 계수와 좌표를 받고 있습니다.
2) 두 번째 if문에서 패러미터로 받은 x와 y가 a,b로 정의된 타원 곡선 위의 점인지 확인합니다.
3) 무한대를 의미하는 None은 이후 점 덧셈의 연산에서 ‘항등원’에 해당하는 무한원점을 다루는 것입니다. 두 점의 덧셈 파트에서 다룰 내용입니다. 무한대라고 생각하시면 됩니다.
- 점의 덧셈
점의 덧셈은 타원곡선에서 가장 주요하게 다루어지면서 가장 유용한 점이기도 합니다. 벡터 연산을 하는 것이 아닌, 새로운 제 3의 점을 얻는 과정으로 생각하시면 될 것 같습니다. '덧셈'이라는 것은 연산의 이름으로 붙여진 것으로 생각하면 됩니다. 개략적으로 그 개요를 설명해 보자면 다음과 같습니다.
곡선 위의 점 A와 점B를 “더한다” =
-
점 A와 점 B를 잇는 직선을 그린다.
-
그 직선이 곡선과 만나는 또다른 점 C를 발견한다.
-
그 점 C를 X축 대칭이동한다.
점 A와 B를 더하는 과정. 직접 그렸더니 이상하다.
즉, A+B = C에서 C는 새롭게 발견되는 곡선위의 점입니다. 그러다 보니, 점 “A” 와 점 “B”를 잇는 직선의 입장에서 생각해 보았을 때, 이 직선과 곡선의 위치는 다음과 같이 4가지의 분류가 있을 수 있습니다. 막 외우려고 생각한다기 보다는 '직선'과 곡선이 만나는 경우는 이런 경우가 있을 수 있겠구나 정도로 생각하시면 될 것 같습니다.
1) 곡선과 한점에서 만나는 경우
2)곡선과 세 점에서 만나는 경우
가장 일반적으로 떠오르는 경우
3)곡선과 두 점에서 만나는데 Y축과 평행한 경우
그림에서 점 두개를 이었는데 그럼 세번 째 점은 어디에 있을까?
4) 곡선과 두 점에서 만나는데 한점이 곡선과 접점인 경우
구현을 위해서는 대충 이러한 관계가 있을 수 있겠구나를 염두하시면 이해가 편합니다. 이러한 덧셈은 덧셈의 결과를 쉽게 예측할 수 없다는 것을 특징으로 가집니다. 이를테면, 비선형 연산의 특징을 가지고 있는 것이죠.
- 점 덧셈 성질
점 덧셈은 일반덧셈과 유사하게 만족하는 성질이 있습니다.
1) 항등원 존재
어떤 점 A에 다른점 I를 더했을 때, A를 나오게 하는 I가 존재한다는 것입니다. 대수의 0과 같은 의미의 점이 존재한다고 보면 됩니다. 이 점을 무한원점이라고 합니다. 그리고 이는 역원이 존재한다는 뜻도 됩니다. A의 역원인 -A를 더했을 때 I가 나오는 점이 존재한다는 것이죠. Point 클래스를 구현한 부분에서 x좌표와 y좌표가 None, 즉 무한대인 경우 그 이후의 조건을 더이상 확인하지 않습니다. 바로 이 항등원 부분을 고려한 것입니다.
이 그림을 보면 이해할 수 있습니다. 그림에서는 약간 짤렸지만 Y축과 평행하는 직선이 지금 두 점에서 타원곡선과 만나고 있는데, 그렇다면 세 번째 점은 어디 있을지 상상을 해보면, ‘무한대’에 있다고 생각할 수 있습니다.
2) 교환법칙
교환법칙은 연산의 순서를 바꿔도 결과가 같다는 뜻입니다. 그림을 보면 점의 순서가 달라진다고 해서 결과가 바뀌지는 않습니다.3) 결합법칙 성립
결합법칙은 (A+B)+C 와 A+(B+C)가 같다는 의미입니다. 직관적이지는 않을수도 있지만, 그림을 직접 그려보면 이해할 수 있습니다.구현
직접 코딩하기 위해서는 총 3가지의 경우로 나누어서 생각하면 됩니다.
1) 두 점이 x축에 수직인 직선 위에 있는 경우(Y축에 평행하는 경우, 1)의 그림)
2) 두 점이 x축에 수직인 직선 위에 있지 않은 경우
3) 두 점이 같은 경우 입니다. 각각에 대한 구현은 다음과 같습니다.
- 두 점이 X축에 수직인 직선 위에 있는 경우
항등원에 대한 연산을 고려하여 add 메서드를 작성합니다.
1) 위에서 Point class의 생성자 부분에서 만약 무한대가 들어오더라도 객체가 생성되도록 처리를 했습니다. 따라서, self 즉 자기 자신이 무한대라면 other이 그대로 나오도록, 혹은 other가 무한대라면 자기 자신이 그대로 나오도록 합니다.
2) 역원에 대한 덧셈은 두 점 x가 같고 y가 다른경우, 즉 위의 그림중에서 두 점을 이은 직선이 x축에 수직인 경우에 해당합니다. 그러할 경우에는 None 값을 가지는 무한 원점을 반환합니다.
-
두 점이 X축에 수직인 직선 위에 있지 않은 경우
이 경우는 간단합니다. 두 점을 지나가는 직선의 기울기를 유도하고, 그 기울기를 통해서 새로운 점의 위치를 계산하면 됩니다. 중학교 수준에서 배운 기울기 공식을 그대로 코드로 구현하면 됩니다. A=(x1,y1) B=(x2,y2) C=(x3,y3) 일 때, A+B = C 이라고 하고 기울기를 s라고 한다면 다음과 같은 식이 유도됩니다.
왜 브런치는 수식 입력을 지원하지 않을까..
사실 기울기를 구해서 공식을 유도하는 과정은 어렵지 않으니 따로 다루지는 않겠습니다. 다만, 우리가 정의한 덧셈은 마지막에 x축 대칭을 해야합니다. (위의 공식에 이미 반영되어 있습니다)
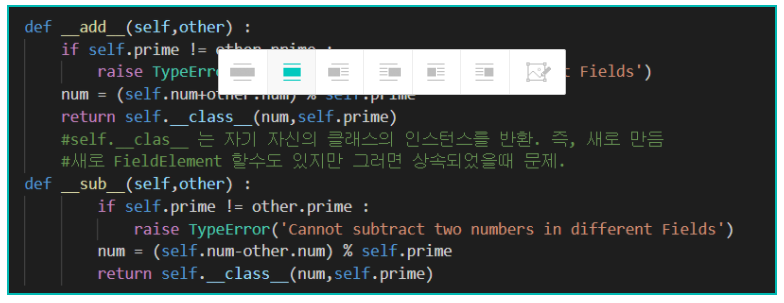
위에서의 add 메서드에 계속 이어집니다
3. 두 점이 같은 경우
두 점이 같은 경우 접선을 구하면 된다.
두 점이 같은 경우의 그래프를 살펴보면, ‘접선’이 그려지는 경우인 것을 알 수 있습니다. 접선의 기울기는 미분을 통해서 구할 수 있습니다. 위의 경우와 마찬가지로 A,C의 경우가 있다고 생각하면(A와 B가 같은 점인 경우이기 때문에) 기울기 s는 미분을 통해서 다음과 같이 구할 수 있습니다. 이정도는 다들 할 수 있을거라 생각합니다 ㅎㅎ
미분을 통해서 얻은 결과
위의 공식을 그대로 옮겨놓은 코드
오타 발견)
2*self.y를 괄호로 묶어줘야 합니다. 안그러면 순서대로 계산이 되어버리기 때문에, 앞은 FieldElement/2가 먼저 계산이 되어버리기 때문입니다. -
마지막 예외처리
마지막으로, 우리가 사용하는 타원곡선 함수는 만약 접선이 x축에 수직인 경우에 y 좌표가 0이 되어 버리기 때문에 기울기를 구할 때 분모가 0이 되어버립니다. 이러한 경우를 예외처리합니다. 무한원점을 반환합니다.
여기까지가 전부 add메서드 안에 들어있는 겁니당
이렇게 챕터2가 마무리되었습니다. 중고등학교 수학 내용정도만 알면 충분히 이해할 수 있기 때문에 크게 어려운 부분은 아니었습니다. 개인적으로 챕터3 차원곡선 암호 부분이 어려웠고 이 부분을 더 정확하게 이해하기 위해서는 챕터 1,2 를 꼼꼼하게 알아야 할 것 같아서 최대한 자세하게 다루었습니다. 그럼 챕터3에서부터는 본격적으로 타원곡선과 유한체를 활용해서 공개키와 암호키에 관련한 ‘타원곡선 암호’를 다루어 보겠습니다
