위키백과에 따르면 Stack을 다음과같이 정의하고 있다. 스택은 추상 자료구조이며 두가지 원리에 의해 동작한다.
In computer science, a stack is an abstract data type that serves as a collection of elements, with two principal operations:
- push, which adds an element to the collection, and
- pop, which removes the most recently added element that was not yet removed.
특징
기본 특징
- 선형 자료구조
- LIFO(Last-In-First-Out)
- push와 pop은 오직 모두 stack의 top인 구조의 끝에서 동작한다.
Non-essential operations
스택에는 필수 기능과 필수 기능이 아닌것들로 나뉜다. 위에서 언급한 push()와 pop()이 필수로 필요한 기능이다. 필수 기능이 아닌것들로는 스택의 맨위의 원소를 조회하는 top() 또는 peek()이 존재하고, 스택의 원소가 비어있는지 확인하는 isEmpty()기능 등이 존재한다.
Overflow
스택은 용량이 제한되도록 구현될 수 있다. 이 때, 용량이 꽉찾을경우 원소를 push()할 경우 overflow error가 발생한다. 이 때는 용량을 늘리거나 pop()을 이용해서 원소를 제거한 후 push()하는 방법이 있다. 흔히 알고있는 깊이 우선 탐색(DFS)를 구현할 때 재귀로 구현하는데, 이 때 Stack overflow가 종종 발생하곤한다.
Underflow
스택이 비어있을경우에 pop() 또는 top()를 수행한다면 underflow error가 발생한다. 즉, 존재하지않는 원소에 접근하기 때문에 발생하는 에러다. 이때는 isEmpty()로 스택이 비어있는지 확인하여 에러를 방지한다.
복잡도
| 자료구조 | 공간복잡도 |
|---|---|
| 스택 | O(n) |
| 큐 | O(n) |
| 기능 | 시간복잡도 |
|---|---|
| push() | O(1) |
| pop() | O(1) |
| peek() | O(1) |
| isEmpty() | O(1) |
| size() | O(1) |
구현
Stack은 Array 또는 singly linked List로 구현하는 두가지 방법이 있다.
Array
스택을 배열을 통해 구현할때는 3가지 요소를 베이스로 구현된다.
structure stack:
maxsize : integer
top : integer
items : array of item- 스택의 용량을 체크해주는 maxsize
- 원소의 가장 위를 나타내주는 top
- 원소들의 데이터 정보를 가지는 items
추가적으로 top은 중요한 기능을 한다. 배열은 보통 0번째 인덱스부터 시작하는데, 처음 top의 값도 0이기 때문에 원소의 개수를 가리키는 동시에 다음 원소가 들어갈 인덱스의 역할을 한다.
자바로 구현해보면 다음과 같다.
/**
*
* @author junho
*
* @param <T>
* Array로 Stack 구현하기
*/
@SuppressWarnings("unchecked")
public class ArrayStack<T> implements IStack<T> {
private static final int maxSize = 1024;
private T[] array = (T[]) new Object[maxSize];
private int size = 0;
@Override
public boolean push(T value) {
if(isFull()) { // overflow
return false;
}
else {
array[size++] = value;
}
return true;
}
@Override
public T pop() {
if(isEmpty()) { // underflow
return null;
}
else {
T ret = array[--size];
return ret;
}
}
@Override
public T peek() {
if(isEmpty()) { // underflow
return null;
}
else {
return array[this.size];
}
}
@Override
public void clear() {
size = 0;
}
@Override
public boolean isEmpty() {
if(size == 0) {
return true;
}
else {
return false;
}
}
@Override
public boolean isFull() {
if(size == maxSize) {
return true;
}
else {
return false;
}
}
@Override
public int size() {
return size;
}
}Singly linked List
스택을 단순 연결 리스트를 통해 구현할때는 2가지 요소를 베이스로 구현된다.
structure Node: // 단순 연결 리스트 구조
data : item
next : frame or nil
structure stack: // Stack 베이스 구조
head : frame or nil
size : integer- 스택의 top을 의미하는 head
- head 노드 내부에 다음 원소를 가리키는 포인터 next
- head 노드 내부에 가지고 있는 원소 data - 스택의 용량을 체크해주는 size
여기서 중요한 점은 head 노드를 스택에서의 top을 의미하게 구현했다는 점이다. 그에 따라서 메모리의 한계가 오지않는 이상 overflow의 개념이 없다.
class Node<T> {
T data;
Node<T> next;
public Node() {}
public Node(T data, Node<T> next) {
this.data = data;
this.next = next;
}
}
/**
*
* @author junho
*
* @param <T>
* Singly LinkedList로 Stack 구현하기
*/
public class LinkedListStack<T> implements IStack<T> {
private Node<T> head;
private int size;
public LinkedListStack() {
head = null;
size = 0;
}
@Override
public boolean push(T value) {
Node<T> newNode = new Node<T>(value,head);
head = newNode;
size++;
return true;
}
@Override
public T pop() {
if(isEmpty()) { // underflow
return null;
}
else {
T elem = head.data;
head = head.next;
size--;
return elem;
}
}
@Override
public T peek() {
if(isEmpty()) {
return null;
}
else {
return head.data;
}
}
@Override
public void clear() {
size = 0;
head = null;
}
@Override
public boolean isEmpty() {
if(head == null) {
return false;
}
else {
return true;
}
}
@Override
public boolean isFull() {
return false; // 단순 연결리스트를 통한 스택 구현은 메모리의 한계가 아닌이상 overflow가 없다.
}
@Override
public int size() {
return size;
}
}사용 예시
두개의 스택으로 큐만들기
큐는 FIFO의 특징을 가지고 있기 때문에 LIFO의 특징을 가진 스택의 반대로 생각해보면 간단하다.
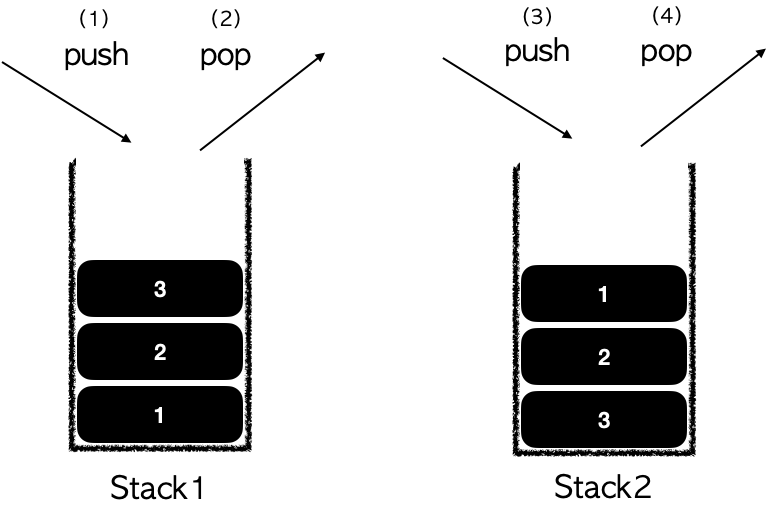
사진과 같이 Stack2에서 빠져나온 순서는 결국 큐와 같다. 단, 구현할때 stack2가 한번 채워졌다면 비기전에 stack1에 원소가 들어온다고해도 stack2에게 넘긴다면 FIFO가 성립이 안되니 유의한다.
import java.util.Stack;
/**
*
* @author junho
* Stack 두개로 Queue 구현하기
*/
public class QueueByStack {
public static class MyQueue<T> {
private Stack<T> stack1; // 원소가 처음 들어가는 스택
private Stack<T> stack2; // pop시에 큐처럼 나온다
MyQueue() {
stack1 = new Stack<>();
stack2 = new Stack<>();
}
void offer(T item) {
stack1.push(item);
}
T pop() {
// stack2가 비기전까지는 stack1에 원소가 들어와도 넘기면 안된다. (큐의 특성을 잃음)
if (stack2.isEmpty()) {
while (!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
}
return stack2.pop();
}
boolean isEmpty() {
if(stack1.empty() && stack2.empty()) {
return true;
}
return false;
}
}
public static void main(String[] args) {
MyQueue<Integer> q = new MyQueue<>();
q.offer(1);
q.offer(2);
q.offer(3);
while(!q.isEmpty()) {
System.out.println(q.pop());
}
}
}역추적
특정 타겟을 찾기위해서 top에서부터 찾아나간다. 만약 도중에 잘못된 경로에 진입했다면 진행을 멈추고 다음 길을 추적한다. 쉽게 말해서 깊이 우선탐색(DFS)가 될수 있다. 이 알고리즘에는 가지치기가
포함될수도있다.

