[자료구조] 힙(heap)

이진 힙(binary heap)은 우선순위 큐(priority queue)를 위한 자료구조다. 그런데 왜 우선순위 큐는 기존에 있는 큐와 같은 방식을 이용하지않고 heap이라는 자료구조를 이용하는 것일까?

그에 대한 답은 우선순위 큐라는 이름에서 찾아볼 수 있다. 큐이긴 큐이지만 삽입된 데이터는 매번 정해진 순서에 따라 정렬이된다. 이 때, 정렬에 시간이 오래걸리는 선형 배열이 아니라 트리의 구조를 가지므로 O(logN)의 시간복잡도로 정렬을 할 수 있다.

이 때, 이진 힙(binary heap)은 완전 이진탐색 트리로서 부모의 우선순위가 자식의 우선순위보다 높은 자료구조다. 다만, 이진 탐색 트리(binary search tree, BST)와 다른점은 자식 노드간의 순서가 정해져있고 부모노드와 크기가 같을 수 있다는 점이다.

---

정의

위키피디아에 따르면 binary heap은 아래와 같은 두 가지 제약조건이 존재하는 이진트리라고 소개한다.

• Shape property: a binary heap is a complete binary tree; that is, all levels of the tree, except possibly the last one (deepest) are fully filled, and, if the last level of the tree is not complete, the nodes of that level are filled from left to right.
• Heap property: the key stored in each node is either greater than or equal to (≥) or less than or equal to (≤) the keys in the node's children, according to some total order.

1. 완전 이진 트리다.
2. 자식 노드는 부모노드보다 작거나 같기만(크거나 같기만)하면 된다.

또한, 이진 힙은 루트노드가 최대인 최대힙 또는 루트노드가 최소인 최소힙으로 분류할 수 있다.

구현

완전이진트리는 1차원 배열로 구현하며, 배열의 두 번째 원소부터 사용한다.

삽입

다음 세가지 원리로 구현된다.

1. Add the element to the bottom level of the heap at the most left.
2. Compare the added element with its parent; if they are in the correct order, stop.
3. If not, swap the element with its parent and return to the previous step.

즉, 가장 왼쪽 밑에 새로운 노드가 삽입된다면 upHeap()이라는 알고리즘에 의해 정렬된다. 자신과 부모노드와 크기를 비교하며 자리를 찾아가는 알고리즘이다.

최대힙을 구성하는 완전트리구조안에서 X에 15라는 숫자를 삽입해보자.

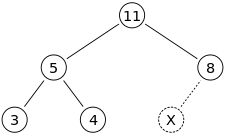
이후의 동작은 15와 부모노드인 8과 비교를 시작한다. 15 > 8 이므로 15와 8을 swap한다.

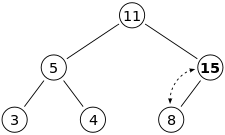
마찬가지로 15는 부모노드 11과 비교해서 swap 판별 여부를 판단하고 swap한다.

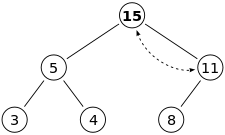
이 예제에서 보다시피 depth level이 3일때 2번의 연산으로 정렬을 했다. 따라서 시간 복잡도는 worth-case일 때 O(logN)인 것을 확인할 수 있다.

	@Override
	public void add(T value) {
		// overflow 방지를 위한 size 재정의
		if(size >= array.length) {
			grow();
		}
		
		array[++size] = value;
		upHeap(size);
	}


	@Override
	public void upHeap(int idx) {
		int nodeIndex = idx;
		T value = this.array[nodeIndex];
		
		if(value == null) return;	// 해당 인덱스의 데이터가 없을 경우
		
		// 루트 노드가 아니면서 부모노드가 자식노드보다 클 경우에
		while(idx > 1 && greater(idx/2,idx)) {
			swap(idx/2,idx);
			idx = idx/2;
		}
	}

삭제

다음 세가지 원리로 구현된다.

1. Replace the root of the heap with the last element on the last level.
2. Compare the new root with its children; if they are in the correct order, stop.
3. If not, swap the element with one of its children and return to the previous step. (Swap with its smaller child in a min-heap and its larger child in a max-heap.)

큐이기때문에 삭제는 항상 루트노드에서 이루어진다. 삭제 된 노드의 위치를 채우기위해서 한칸씩 인덱스를 당기는 것이 아니라, 맨 마지막 인덱스의 리프노드를 루트노드로 가져온다.

그 이후로 downHeap()을 통해서 루트 노드에 새로 차지한 데이터를 적절히 배분해준다. 아래는 삭제연산의 예제이다.

먼저 부모노드를 삭제해보자.

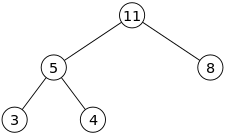
부모노드를 삭제한 뒤에는 가장 마지막인덱스의 노드 데이터를 부모노드로 올린다.

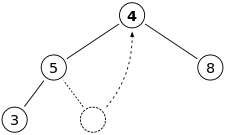
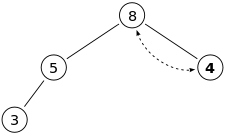
이후에는 부모노드와 자식노드를 비교해서 만약, 자식노드가 더 클 경우 swap한다.(최대힙 기준)

	@Override
	public T remove() {
		T value = array[1];	
		swap(1,size--);		// size 1 감소 및 마지막 노드와 부모노드 스왑
		array[size+1] = null;
		
		downHeap(1);
		return value;
	}


	@Override
	public void downHeap(int idx) {
		T value = array[idx];
		if (value == null) return;
		
		int leftIdx = 2 * idx;
		int rightIdx = 2 * idx + 1;
		
		T left = (leftIdx != Integer.MIN_VALUE && leftIdx < this.size) ? this.array[leftIdx] : null;
		T right = (rightIdx != Integer.MIN_VALUE && rightIdx < this.size) ? this.array[rightIdx] : null;
		
		T nodeToMove = null;
		int nodeToMoveIdx = -1;
		
		// 두 자식 노드가 모두 크거나 같을 때
		if((type == Type.MIN && left != null && right != null && value.compareTo(left) > 0 && value.compareTo(right) > 0) 
			|| (type == Type.MAX && left != null && right != null && value.compareTo(left) < 0 && value.compareTo(right) < 0)) {
			
			// 오른쪽 자식노드가 왼쪽 자식노드보다 크거나 작을 때
			if((right != null) &&
				((type == Type.MIN && (right.compareTo(left) < 0)) || ((type == Type.MAX && right.compareTo(left) > 0)))) {
				nodeToMove = right;
				nodeToMoveIdx = rightIdx;
			}
			
			// 왼쪽 자식노드가 오른쪽 자식노드보다 크거나 작을 때
			else if((left != null) && 
				((type == Type.MIN && left.compareTo(right) < 0)) || (type == Type.MAX && left.compareTo(right) > 0)) {
				nodeToMove = left;
				nodeToMoveIdx = leftIdx;
			}
			
			// 두 자식노드가 같을 때
			else {
				nodeToMove = right;
				nodeToMoveIdx = rightIdx;
			}
		}
		
		// 오른쪽 자식 노드가 부모노드보다 크거나 같을 때
		else if((type == Type.MIN && right != null && value.compareTo(right) > 0)
				|| (type == Type.MAX && right != null && value.compareTo(right) < 0)) {
			nodeToMove = right;
			nodeToMoveIdx = rightIdx;
		}
		
		// 왼쪽 자식 노드가 부모노드보다 크거나 같을 때
		else if((type == Type.MIN && left != null && value.compareTo(left) > 0) 
			|| (type == Type.MAX && left != null && value.compareTo(left) < 0)) {
				nodeToMove = left;
				nodeToMoveIdx = leftIdx;
		}
		
		// 교환할 노드가 없을 경우
		if(nodeToMove == null) return;
		
		// 스왑
		this.array[nodeToMoveIdx] = value;
		this.array[idx] = nodeToMove;
		
		downHeap(nodeToMoveIdx);
	}

응용

실생활에서는 데이터의 우선순위를 다루는 상황에서 많이 사용된다. 대표적으로는 실시간 급상승 검색어 제공을 위한 적절한 자료구조다. 또한 힙정렬, MST의 Prim, 그래프이론 그리디의 다익스트라 등에서 활용된다.