[python] 게임 맵 최단거리

문제 설명

ROR 게임은 두 팀으로 나누어서 진행하며, 상대 팀 진영을 먼저 파괴하면 이기는 게임입니다. 따라서, 각 팀은 상대 팀 진영에 최대한 빨리 도착하는 것이 유리합니다.

지금부터 당신은 한 팀의 팀원이 되어 게임을 진행하려고 합니다. 다음은 5 x 5 크기의 맵에, 당신의 캐릭터가 (행: 1, 열: 1) 위치에 있고, 상대 팀 진영은 (행: 5, 열: 5) 위치에 있는 경우의 예시입니다.

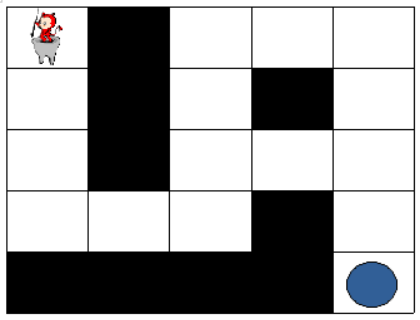
위 그림에서 검은색 부분은 벽으로 막혀있어 갈 수 없는 길이며, 흰색 부분은 갈 수 있는 길입니다. 캐릭터가 움직일 때는 동, 서, 남, 북 방향으로 한 칸씩 이동하며, 게임 맵을 벗어난 길은 갈 수 없습니다.
아래 예시는 캐릭터가 상대 팀 진영으로 가는 두 가지 방법을 나타내고 있습니다.

• 첫 번째 방법은 11개의 칸을 지나서 상대 팀 진영에 도착했습니다.

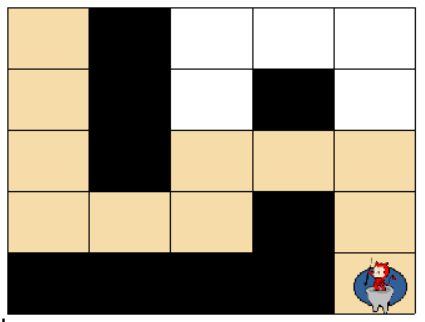
• 두 번째 방법은 15개의 칸을 지나서 상대팀 진영에 도착했습니다.

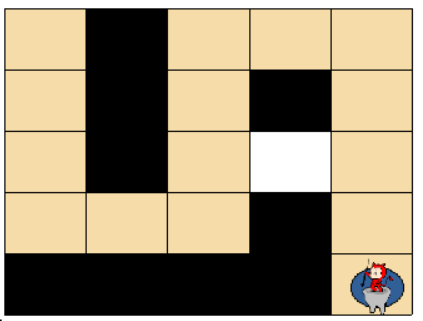
위 예시에서는 첫 번째 방법보다 더 빠르게 상대팀 진영에 도착하는 방법은 없으므로, 이 방법이 상대 팀 진영으로 가는 가장 빠른 방법입니다.

만약, 상대 팀이 자신의 팀 진영 주위에 벽을 세워두었다면 상대 팀 진영에 도착하지 못할 수도 있습니다. 예를 들어, 다음과 같은 경우에 당신의 캐릭터는 상대 팀 진영에 도착할 수 없습니다.

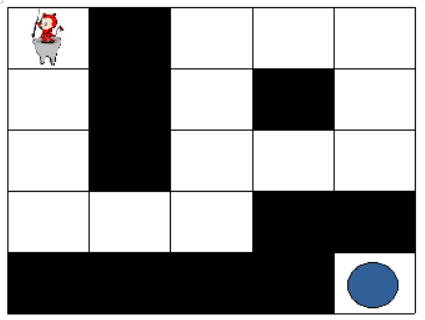
게임 맵의 상태 maps가 매개변수로 주어질 때, 캐릭터가 상대 팀 진영에 도착하기 위해서 지나가야 하는 칸의 개수의 최솟값을 return 하도록 solution 함수를 완성해주세요. 단, 상대 팀 진영에 도착할 수 없을 때는 -1을 return 해주세요.

나의 풀이( 다익스트라 활용 )

import collections
import heapq
def solution(maps):
    n , m = len(maps) , len(maps[0])
    big_map = [0] * (n+2) * (m+2)
    cur_list = []
    cursor = m + 3
    start , fin = [m+3 , (n+2)*(m+2) - m - 4]
    
    # 7*7 행렬제작 후 기존 maps에 한겹 더 둘러싸기
    for i in range(len(maps)):
        for j in maps[i]:
            cur_list.append(cursor)
            big_map[cursor] = j
            cursor +=1
        cursor += 2

    # 그래프 인접 리스트 구성
    graph = collections.defaultdict(list)
    for k in cur_list:
        if big_map[k] == 1:
            if big_map[k-(m+2)] == 1:  # 상
                graph[k].append(k-(m+2))
            if big_map[k-1] ==1 :  # 좌
                graph[k].append(k-1)
            if big_map[k+1] == 1:  # 우
                graph[k].append(k+1)
            if big_map[k+m+2] == 1: # 하
                graph[k].append(k+m+2) 
                
    # 큐 변수: [(거리, 정점)]
    Q = [(1,start)]
    
    dist = collections.defaultdict(int)
    
    # 우선순위 큐 최솟값 기준으로 도착점까지 최소 거리 판별
    while Q:
        result, node = heapq.heappop(Q)
        if node == fin:
            return result
        
        if node not in dist:
            dist[node] = result
            for v in graph[node]:
                alt = result + 1
                heapq.heappush(Q,(alt,v))
                
    return -1

• 일단 기본 제공된 maps에서 한겹을 더 둘러싼 0으로 이루어진 직사각형을 만들었다. 그리고 maps의 값들을 중간에 배치시켰다. ( 0 으로 한바퀴 감싸도록 )

• 그리고 n * m 개의 직사각형의 각각의 칸이 노드라고 생각하고 그래프 인접 리스트를 제작했다. 1이 있는 곳만 갈 수 있는 지점이라 간주하고 딕셔너리를 만들었다. (defaultdict 이용)

• 다익스트라 알고리즘을 활용하여 최단경로를 구했다.

• dist라는 딕셔너리를 활용해 이미 최단거리로 갔던 노드(칸)은 다시 방문하지 않도록 설정했고, 만약 정점이 원하는 도착지와 일치하면 그때의 최소값을 return하도록 설정했다.

• 그리고 while문이 종료되도록 도착하지 못하면, 목적지로 도착할 수 없는 것이므로 -1을 리턴했다.