[python] 그래프 - (1)

그래프란?

객체의 일부 쌍들이 '연관되어' 있는 객체 집합 구조

그래프 이론의 시작에는 대표적으로 오일러 경로와 해밀턴 경로가 있다.

• 오일러 경로는 정점과 그 정점들을 잇는 간선이 존재하고 모든 간선을 한번씩 지나는 경로를 뜻한다. 우리나라에서는 어렸을 때 주로 했던 '한붓그리기'라고 생각하면 쉽다.

• 해밀턴 경로는 각 정점을 한 번씩 방문하는 무향 또는 유향 그래프 경로를 말한다.

• 오일러 경로와 해밀턴 경로의 차이점을 들자면, 오일러 경로는 간선을 기준으로 하고 해밀턴 경로는 정점을 기준으로 한다는 점이다.

코딩 테스트를 진행할 때 대부분의 그래프 탐색은 DFS( 깊이 우선 탐색, Depth-First Search )를 주로 사용할 예정이다.

그래프를 표현하는 방법에는 인접 리스트와 인접 행렬이 있다. 인접 리스트로 표현하면 파이썬의 딕셔너리 자료형으로 나타낼 수 있다.

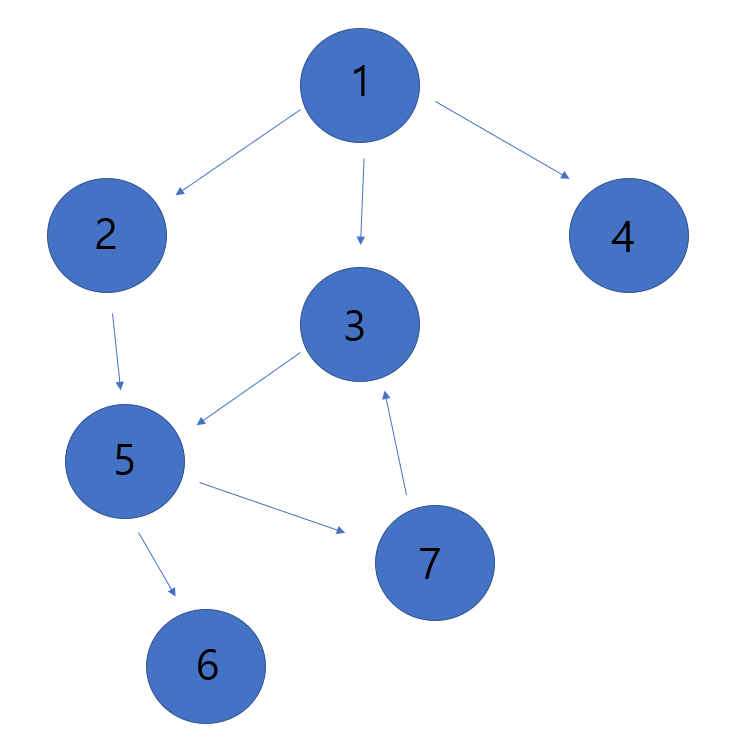
<예시 그래프 >

DFS ( 깊이 우선 탐색 )

일반적으로 DFS 는 스택으로 구현하며, 재귀를 이용하면 좀 더 간단하게 구현할 수 있다. 코딩 테스트 시에도 재귀 구현이 더 선호되는 편이다.

재귀 구조로 표현

graph = {
    1:[2,3,4],
    2:[5],
    3:[5],
    4:[],
    5:[6,7],
    6:[],
    7:[3],
    }



# 정점 v의 모든 인접 유향 간선들을 반복
def recursive_dfs(v,discovered=[]):
    discovered.append(v)
    for w in graph[v]:
        if not w in discovered:
            discovered = recursive_dfs(w,discovered)
    return discovered

예시 그래프 실행
f'recursive dfs:{recursive_dfs(1)}'

예시 그래프 DFS 결과

'recursive dfs: [1,2,5,6,7,3,4]'

• graph 는 예시 그래프를 인접 리스트로 표현한 것이다.
• DFS 수도코드를 파이썬 버전으로 바꾼 방식이다.
• 탐색이 총 3번에 걸쳐 진행됐는데, 1->2->5->6 까지 진행하고 , 되돌아 갔다가 7->3 , 다시 도될아 나가 마지막으로 4 를 탐색하는 결과가 도출되었다.

스택을 이용한 반복 구조로 구현

def iterative_dfs(start_v):
    discovered= []
    stack = [start_v]
    while stack:
        v = stack.pop()
        if v not in discovered:
            discovered.append(v)
            for w in graph[v]:
                stack.append(w)
    
    return discovered

f'iterative dfs:{iterative_dfs(1)}'

'iterative dfs: [1,4,3,5,7,6,2]'

같은 DFS 인데 재귀 구조와 스택 구조가 결과가 다른 이유는 재귀 DFS 는 사전식 순서로 방문한 데 반해 반복 DFS 는 역순으로 방문했기 때문이다. 스택을 구현했기 때문에 가장 마지막에 삽입된 노드부터 꺼내서 반복하게 된다.

BFS ( 너비 우선 탐색 )

다음은 BFS를 구현해보자. BFS는 DFS에 비해 쓰임새는 적지만 최단 경로를 찾는 다익스트라 알고리즘 등에 매우 유용하게 쓰인다.

큐를 이용한 반복 구조로 구현

BFS 는 재귀를 이용해 구할 수 없고 오직 큐를 이용하는 반복 구현만 가능하다.

def iterative_bfs(start_v):
    discovered = [start_v]
    queue = [start_v]
    while queue:
        v = queue.pop(0)
        for w in graph[v]:
            if w not in discovered:
                discovered.append(w)
                queue.append(w)
    
    return discovered

f'iterative bfs:{iterative_bfs(1)}'

'iterative bfs: [1,2,3,4,5,6,7]'

• 1 부터 순서대로 각각의 인접 노드를 우선으로 방문하는 너비 우선 탐색이 잘 실행됐음을 확인할 수 있다.

백트래킹

백트래킹은 해결책에 대한 후보를 구축해 나아가다 가능성이 없다고 판단되는 즉시 후보를 포기해 정답을 찾아가는 범용적인 알고리즘으로 제약 충족 문제에 특히 유용하다.

DFS 를 이야기 하면 항상 같이 나오는 백트래킹은 탐색을 하다가 더 갈 수 없으면 왔던 길을 되돌아가 다른 길을 찾는다는 데서 유래했다. 백트래킹은 DFS와 같은 방식으로 탐색하는 모든 방법을 뜻하며, 기본적으로 모두 DFS의 범주에 속한다.

백트래킹은 가보고 되돌아오고를 반복해 브루트 포스와 유사하지만 , 한번 방문 후 가능성이 없는 경우에는 즉시 후보를 포기한다는 점에서 매번 같은 경로를 방문하는 브루스 포스보다는 훨씬 효율적인 방식이다.

• 제약 충족 문제 : 수많은 제약 조건을 충족하는 상태를 찾아내는 수학 문제. ex) 스도쿠 , 십자말 풀이, 4색 문제 등등

문제 1 . 섬의 개수

1을 육지로 , 0을 물로 가정한 2D 그리드 맵이 주어졌을 때, 섬의 개수를 계산하라. ( 연결되어 있는 1의 덩어리 개수를 구하라.)

ex ) 입력 :
11110
11010
11000
00000

출력 : 1

DFS로 그래프 탐색

def numIslands(grid):
    def dfs(i,j):
        # 더 이상 땅이 아닌 경우 종료
        if i < 0 or i >= len(grid) or \
        j < 0 or j >= len(grid[0]) or \
        grid[i][j] != '1':
            return
        
        grid[i][j] = 0
        # 동서남북 탐색
        dfs(i+1, j)
        dfs(i-1 , j)
        dfs(i,j+1)
        dfs(i, j-1)
        
    count = 0
    for i in range(len(grid)):
        for j in range(len(grid[0])):
            if grid[i][j] == '1':
                dfs(i,j)
                # 모든 육지 탐색 후 카운트 1 증가
                count += 1
        
    return count

• 동서남북이 모두 연결된 그래프로 가정하고 동일한 형태로 처리할 수 있으며, 네 방향 각각 DFS 재귀를 이용해 탐색을 끝마치면 1이 증가하는 형태로 육지의 개수를 파악할 수 있다.
• 먼저 중첩함수부터 설명을 하자면, 일단 땅이 아닌 경우 ( i 또는 j가 인덱스를 벗어나거나 값이 1이 아닌경우 ) 종료를 시킨다.
• 동서남북을 모두 탐색하면서 재귀호출하고 , 이렇게 재귀 호출이 백트래킹으로 모두 빠져 나오면 섬 하나를 발견한 것으로 간주한다. 이때 이미 방문했던 곳은 1이 아닌 값으로 마킹한다.
• 지금 여기서는 0으로 마킹을 했는데, 0이 아니어도 #이나 * 같은 1만 아닌 값을 넣으면 된다.
• 그리고 모든 육지 탐색 후 count 를 1 증가 시켜주면 된다.