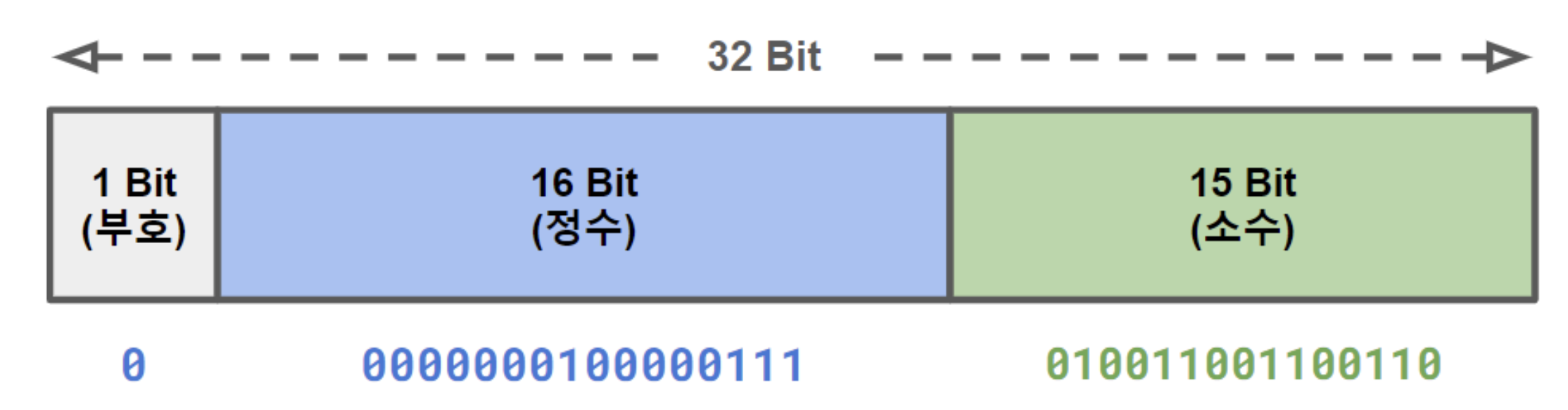
고정 소수점 (Fixed-point)
고정 소수점 수는 소수점의 위치가 고정된 형태로 소수를 표현합니다. 고정된 비트를 정수 부분과 소수 부분에 나누어 사용합니다. 예를 들어, 16비트 고정 소수점 형식에서 8비트를 정수 부분, 나머지 8비트를 소수 부분에 사용할 수 있습니다.
장점
- 고정된 소수점 위치로 인해 연산 속도가 빠르고 단순하다.
- 특정 상황(예: 임베디드 시스템)에서 메모리와 성능 효율이 좋다.
단점
- 표현할 수 있는 수의 범위가 제한적이다.
- 정밀도가 고정되어 있어, 매우 큰 수나 매우 작은 수를 표현하는 데 한계가 있다.
부동 소수점 (Floating-point)
부동 소수점 수는 소수점의 위치가 가변적입니다. 이는 더 넓은 범위의 수를 더 큰 정밀도로 표현할 수 있게 합니다. IEEE 754 표준에 따라, 일반적으로 32비트(단정밀도)와 64비트(double! 배정밀도) 형식이 사용됩니다.
장점
- 매우 큰 수와 매우 작은 수를 표현할 수 있는 넓은 범위를 가진다.
- 높은 정밀도로 다양한 계산을 수행할 수 있다.
단점
- 연산이 복잡하고 느리다.
- 특정 숫자 범위 내에서만 정밀도가 높다.
비교
| 특성 | 고정 소수점 | 부동 소수점 |
|---|---|---|
| 표현 범위 | 제한적 | 넓음 |
| 정밀도 | 고정 | 가변 |
| 연산 속도 | 빠름 | 느림 |
| 메모리 사용 | 적음 | 많음 |
| 복잡도 | 단순 | 복잡 |
🪶 부동 소수점의 표현 방식
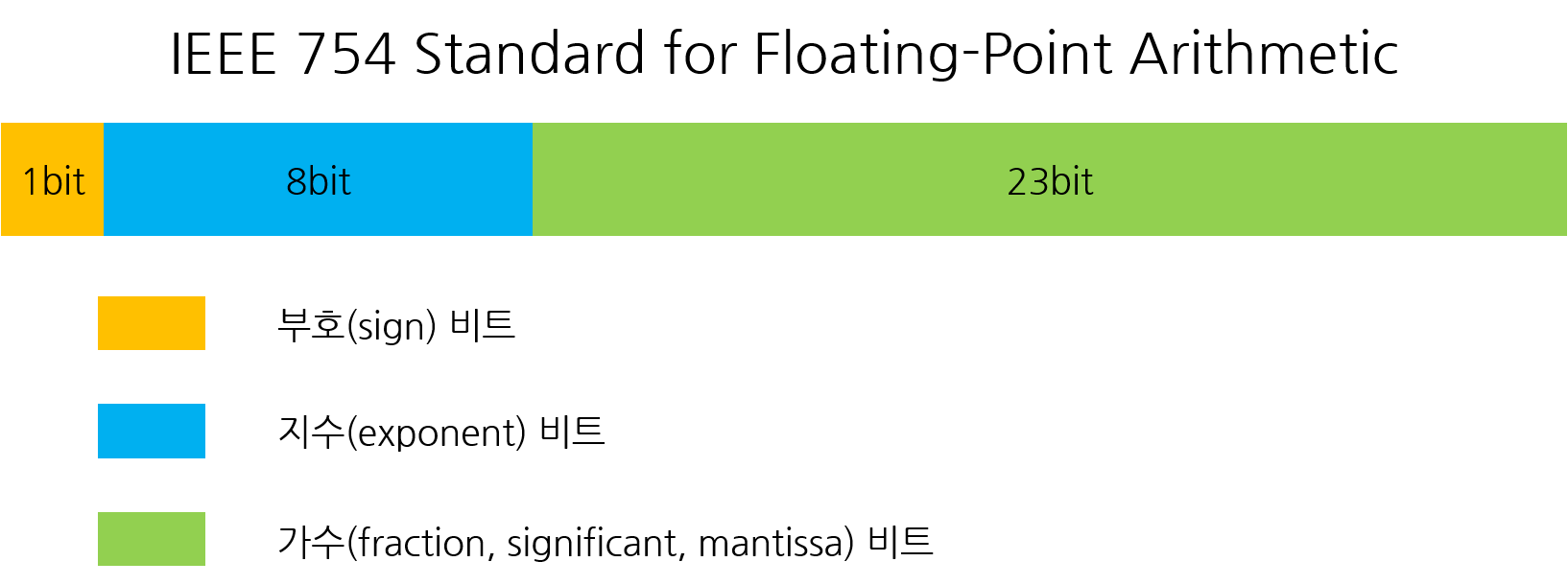

부동 소수점의 표현 방식은 fixed-point 와 유사하다, 하지만 정규화 과정 과 Bias 를 추가하는 과정이 따라 붙는다.
정규화 과정을 통해 지수 표기법 으로 이진수를 나타낸 뒤, 지수 와 bias(32bit) = 127 을 더하여 bias를 추가한다. 위의 그림 예제에서는 지수가 3 이다. (103)
🦉 Bias를 추가하는 이유
그렇다면 자연스럽게 드는 의문이 있을 것이다. Bias는 왜 추가하는 것일까?
부동 소수점 계산에서 Bias 지수를 사용하는 주요 이유는 바로 덧셈 회로 활용을 통한 효율적인 계산 때문 입니다.
덧셈 회로와 🆚 뺄셈 회로
🪃 구조적 차이
덧셈 회로는 간단한 XOR와 AND 게이트로 구성되어 있습니다.
뺄셈 회로는 XOR, AND, NOT 게이트를 조합하여 복잡한 빌림(Borrow) 비트를 계산합니다.
🎢 연산 복잡성
덧셈 회로는 각 비트를 독립적으로 더하는 간단한 연산입니다.
뺄셈 회로는 빌림(Borrow) 비트를 계산해야 하므로 조금 더 복잡한 연산이 필요합니다.
💻 하드웨어 구현
덧셈 회로는 간단한 구조로 이루어져 있어 하드웨어에서 쉽게 구현할 수 있습니다.
뺄셈 회로는 빌림(Borrow) 비트를 계산해야 하므로 구현이 더 복잡합니다.
🙆♂️ 따라서 Bias를 추가하는 이유는 아래와 같습니다.
Bias exponent를 사용하면 부호 없는 수 표현을 통해 실수 연산을 편리하게 할 수 있게 되고,
덧셈 회로의 이점을 이용해서 연산이 단순해집니다.
float의 경우 127(0111_1111)을 더하고,
double의 경우 1023(0011_1111_1111)을 지수에 더합니다.
🐈 꼬리에 꼬리를 무는 질문...
해당 포스트는 처음에 PintOS의 커널단에서는 Fixed-point 연산을 통해 실수를 계산한다고 한 것에서부터 시작됐다.
- fixed-point 방식과 floating-point 방식의 차이.
- floating-point로 표현하는 과정에서 나타난
bias 지수 표기법
앞으로 PintOS를 하면서 궁금한 것이 생기면 이렇게 조금씩 정리를 해놔야겠다! 😼
😊 도움을 준 고마운 사람들 🥳
김광윤 : https://github.com/leorivk
정승호 : https://github.com/seungho-jg
황연경 : https://github.com/yunnn426
전병준 : https://github.com/jun9898